“以學(xué)生為中心”的泰勒公式探究式教學(xué)設(shè)計

劉華 景慧麗

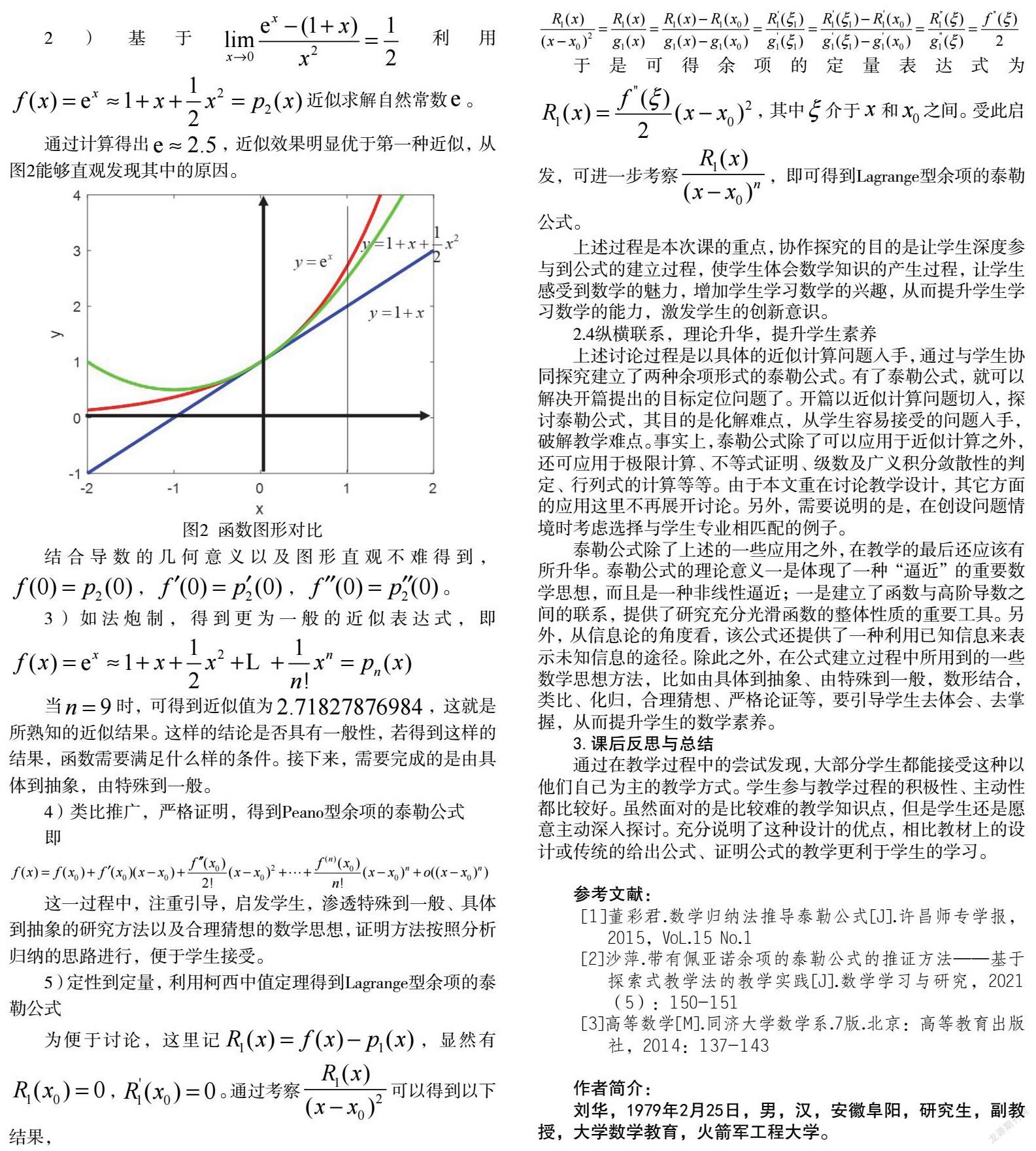
摘要：泰勒公式是高等數(shù)學(xué)課程中的教學(xué)重點和難點，學(xué)生對其總是望而生畏。在教學(xué)設(shè)計中首先充分分析學(xué)生學(xué)情基礎(chǔ)，然后通過自然常數(shù) 的近似計算引入，由淺入深，由具體到抽象，由特殊到一般，引導(dǎo)學(xué)生猜想、論證、協(xié)同探究，逐步建立泰勒公式。讓學(xué)生深度參與公式的建立過程，消除學(xué)生疑惑，化解學(xué)生畏難情緒，從而達(dá)成高效的學(xué)與教。

關(guān)鍵詞：泰勒公式;佩亞諾型余項;拉格朗日型余項;以學(xué)生為中心;探究式

泰勒公式是一元函數(shù)微積分的一個重要內(nèi)容，不僅在理論上占有重要地位，在近似計算、極限計算、函數(shù)性質(zhì)的研究等方面也有重要應(yīng)用。但是，泰勒公式是教學(xué)難點，學(xué)生看到其復(fù)雜的表達(dá)形式更是無所適從。為破解這一教學(xué)難點，筆者從學(xué)生角度出發(fā)，深入分析原因，找出癥結(jié)，進(jìn)行有針對性的教學(xué)設(shè)計。在教學(xué)過程中充分發(fā)揮學(xué)生的主觀能動性，通過問題優(yōu)化設(shè)計，層層遞進(jìn)，在問題的不斷解決過程中，協(xié)同建立泰勒公式。

1.學(xué)情分析

泰勒公式形式復(fù)雜，內(nèi)容抽象，學(xué)生更是對這種表達(dá)形式感到莫名其妙。例如，

以上正是函數(shù) 泰勒展開式的兩種形式，分別是Peano型余項的泰勒公式和Lagrange型余項的泰勒公式。從形式上，學(xué)生不解的是為何要將一個簡單的函數(shù)表示成多項式函數(shù) 與余項 之和的形式？從內(nèi)容上，不理解這樣一個轉(zhuǎn)化有何用途，兩種不同的余項形式本質(zhì)區(qū)別是什么，各有什么應(yīng)用？從理論上，這種轉(zhuǎn)化有何意義，其蘊(yùn)含的思想方法是什么，如何從更高層次理解公式的意義，對學(xué)生來講更是一個巨大的挑戰(zhàn)。

為什么學(xué)生對泰勒公式總是敬而遠(yuǎn)之。從內(nèi)容來看，一方面是因為泰勒公式的表達(dá)形式繁瑣，難以記憶;另一方面是因為對泰勒公式的作用與地位也不理解，不知學(xué)來何用。從學(xué)生自身角度看，學(xué)習(xí)能力有所欠缺，主動學(xué)習(xí)意識不強(qiáng)，學(xué)習(xí)方法亟待改進(jìn)，數(shù)學(xué)符號、數(shù)學(xué)語言的掌握不好，面對這樣一個看似違背常識的復(fù)雜公式更是一頭霧水。

基于上述分析，要達(dá)成較好的教學(xué)效果，實現(xiàn)既定教學(xué)目標(biāo)，必須從學(xué)生角度出發(fā)進(jìn)行教學(xué)設(shè)計。首先基于最近發(fā)展區(qū)理論創(chuàng)設(shè)情境，以問題為牽引，設(shè)疑激趣，誘導(dǎo)啟發(fā)，層層遞進(jìn)，引導(dǎo)學(xué)生共同建立泰勒公式。在問題的解決過程中建立公式，在共同討論的過程中釋疑解惑，在進(jìn)一步的探索中理論升華。

2.以學(xué)生為中心的教學(xué)設(shè)計

2.1創(chuàng)境設(shè)疑，吸引學(xué)生

問題情境的創(chuàng)設(shè)對于問題的解決至關(guān)重要，因此在設(shè)計問題情境時必須充分考慮學(xué)生實際。最近發(fā)展區(qū)理論指出，教學(xué)應(yīng)著眼于學(xué)生的最近發(fā)展區(qū)，搭建學(xué)生現(xiàn)有知識和新知識之間的橋梁，為學(xué)生提供帶有一定難度的問題，通過引導(dǎo)啟發(fā)，激發(fā)學(xué)生潛能，實現(xiàn)對問題的解決，達(dá)成掌握新知識、領(lǐng)悟新方法的教學(xué)目的。

本文所創(chuàng)設(shè)的問題情境是目標(biāo)定位問題。已知雷達(dá)測得目標(biāo)的距離和仰角，計算目標(biāo)的高度（計算結(jié)果需滿足精度要求）。這個問題歸結(jié)于三角函數(shù)的近似計算，學(xué)生在高中時可以通過查表計算？但表中的數(shù)據(jù)是如何獲得的？其精度是否能達(dá)到實際需求？學(xué)生可能根本就沒有想過這樣一個問題。之前的學(xué)習(xí)，更多的是接受，少質(zhì)疑，欠思考，不太會去深入地思考來龍去脈。創(chuàng)設(shè)這樣一個問題情境，可以引起學(xué)生的共鳴，吸引學(xué)生，激發(fā)學(xué)生繼續(xù)學(xué)習(xí)的興趣。

2.2問題驅(qū)動，引導(dǎo)學(xué)生

面對上述問題，學(xué)生可能是滿眼疑惑，無從下手。此時就需要老師通過問題驅(qū)動的方式引導(dǎo)學(xué)生分析問題、解決問題。能否達(dá)成引導(dǎo)的效果，問題設(shè)計很重要，其具體設(shè)計要具有科學(xué)性、層次性、遞進(jìn)性，更重要的還要具有對問題解決的啟發(fā)性。因此，在問題設(shè)計時同樣要考慮學(xué)生已有的知識結(jié)構(gòu)以及思維特點。

因此，在解決上述問題時采取迂回的策略，先討論一個具體的，學(xué)生又相對熟悉的問題，然后再來解決三角函數(shù)的近似計算問題。自然常數(shù) 學(xué)生既熟悉又陌生，知道它是一個無限不循環(huán)小數(shù)，近似等于 ，可這個近似的數(shù)值結(jié)果是怎樣得到的，其誤差又如何，以此問題作為切入點進(jìn)行探討。

2.3協(xié)同探究，幫助學(xué)生

通過式（1），學(xué)生容易知道，令 就可以得到 的近似值，此時問題又轉(zhuǎn)化為式（1）中的多項式是如何得到的？如何估計其誤差？這里結(jié)合學(xué)生的認(rèn)識規(guī)律，遵循由具體到抽象，由特殊到一般的方法，在式（1）中先取 ，即有 。下面結(jié)合數(shù)值計算、幾何觀察、類比推廣、理論證明與學(xué)生一道，協(xié)同探究，建立泰勒公式。

1）基于 利用 近似求解自然常數(shù) 。

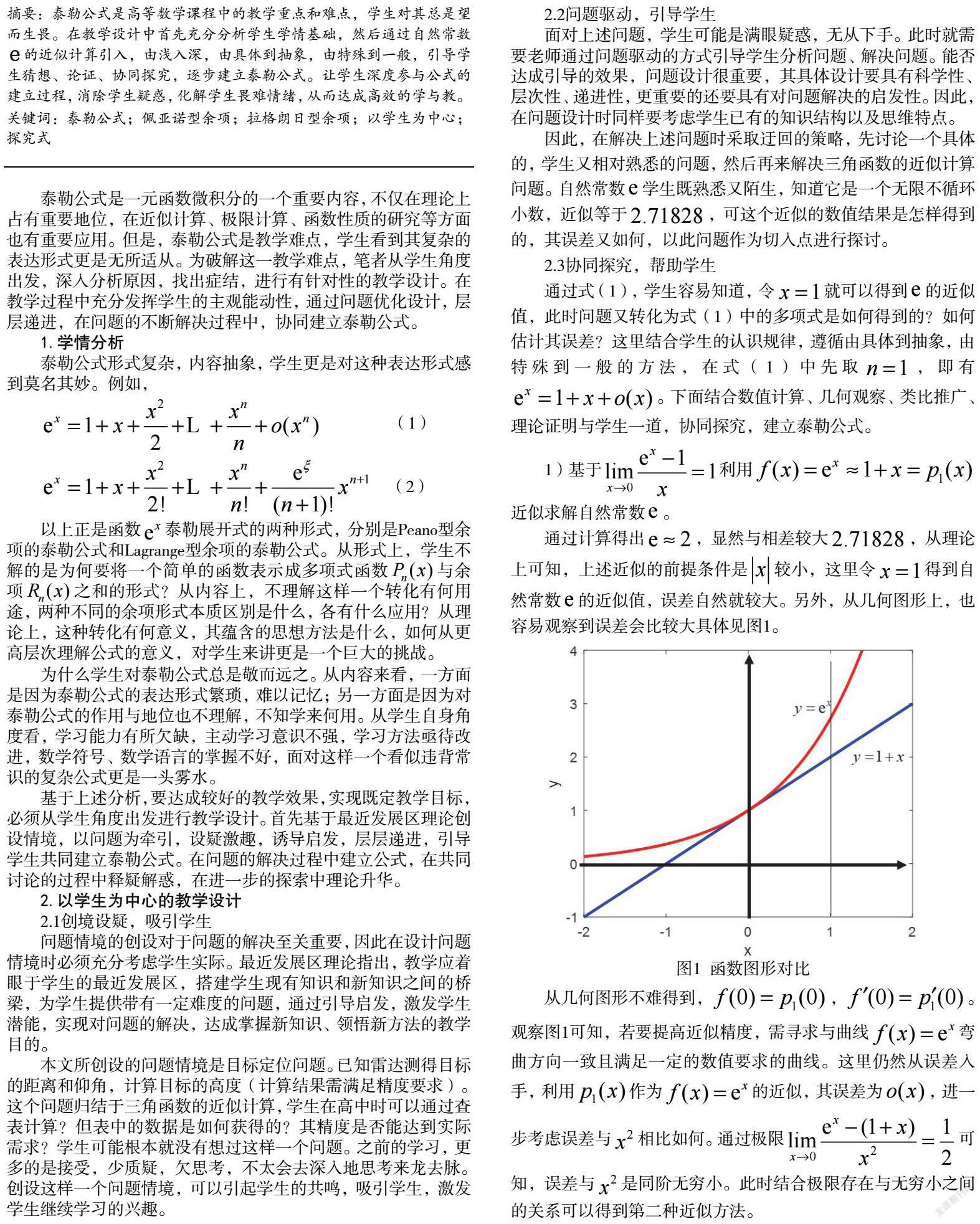
通過計算得出 ，顯然與相差較大 ，從理論上可知，上述近似的前提條件是 較小，這里令 得到自然常數(shù) 的近似值，誤差自然就較大。另外，從幾何圖形上，也容易觀察到誤差會比較大具體見圖1。

上述過程是本次課的重點，協(xié)作探究的目的是讓學(xué)生深度參與到公式的建立過程，使學(xué)生體會數(shù)學(xué)知識的產(chǎn)生過程，讓學(xué)生感受到數(shù)學(xué)的魅力，增加學(xué)生學(xué)習(xí)數(shù)學(xué)的興趣，從而提升學(xué)生學(xué)習(xí)數(shù)學(xué)的能力，激發(fā)學(xué)生的創(chuàng)新意識。

2.4縱橫聯(lián)系，理論升華，提升學(xué)生素養(yǎng)

上述討論過程是以具體的近似計算問題入手，通過與學(xué)生協(xié)同探究建立了兩種余項形式的泰勒公式。有了泰勒公式，就可以解決開篇提出的目標(biāo)定位問題了。開篇以近似計算問題切入，探討泰勒公式，其目的是化解難點，從學(xué)生容易接受的問題入手，破解教學(xué)難點。事實上，泰勒公式除了可以應(yīng)用于近似計算之外，還可應(yīng)用于極限計算、不等式證明、級數(shù)及廣義積分?jǐn)可⑿缘呐卸ā⑿辛惺降挠嬎愕鹊取Ｓ捎诒疚闹卦谟懻摻虒W(xué)設(shè)計，其它方面的應(yīng)用這里不再展開討論。另外，需要說明的是，在創(chuàng)設(shè)問題情境時考慮選擇與學(xué)生專業(yè)相匹配的例子。

泰勒公式除了上述的一些應(yīng)用之外，在教學(xué)的最后還應(yīng)該有所升華。泰勒公式的理論意義一是體現(xiàn)了一種“逼近”的重要數(shù)學(xué)思想，而且是一種非線性逼近;一是建立了函數(shù)與高階導(dǎo)數(shù)之間的聯(lián)系，提供了研究充分光滑函數(shù)的整體性質(zhì)的重要工具。另外，從信息論的角度看，該公式還提供了一種利用已知信息來表示未知信息的途徑。除此之外，在公式建立過程中所用到的一些數(shù)學(xué)思想方法，比如由具體到抽象、由特殊到一般，數(shù)形結(jié)合，類比、化歸，合理猜想、嚴(yán)格論證等，要引導(dǎo)學(xué)生去體會、去掌握，從而提升學(xué)生的數(shù)學(xué)素養(yǎng)。

3.課后反思與總結(jié)

通過在教學(xué)過程中的嘗試發(fā)現(xiàn)，大部分學(xué)生都能接受這種以他們自己為主的教學(xué)方式。學(xué)生參與教學(xué)過程的積極性、主動性都比較好。雖然面對的是比較難的教學(xué)知識點，但是學(xué)生還是愿意主動深入探討。充分說明了這種設(shè)計的優(yōu)點，相比教材上的設(shè)計或傳統(tǒng)的給出公式、證明公式的教學(xué)更利于學(xué)生的學(xué)習(xí)。

參考文獻(xiàn)：

[1]董彩君.數(shù)學(xué)歸納法推導(dǎo)泰勒公式[J].許昌師專學(xué)報，2015，VoL.15 No.1

[2]沙萍.帶有佩亞諾余項的泰勒公式的推證方法——基于探索式教學(xué)法的教學(xué)實踐[J].數(shù)學(xué)學(xué)習(xí)與研究，2021（5）：150-151

[3]高等數(shù)學(xué)[M].同濟(jì)大學(xué)數(shù)學(xué)系.7版.北京：高等教育出版社，2014：137-143

作者簡介：

劉華，1979年2月25日，男，漢，安徽阜陽，研究生，副教授，大學(xué)數(shù)學(xué)教育，火箭軍工程大學(xué)。