題型定位突破 過程分析總結
——以二次函數與角度問題為例
江蘇省蘇州高新區實驗初級中學 周 濤
1 引言
二次函數與角度問題屬于典型問題,通常以拋物線為背景,引入幾何圖形構建幾何角,問題解法較為特殊,具體探究如下.
2 引例探究,分步突破
2.1 引例呈現
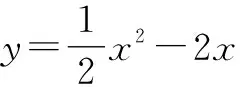
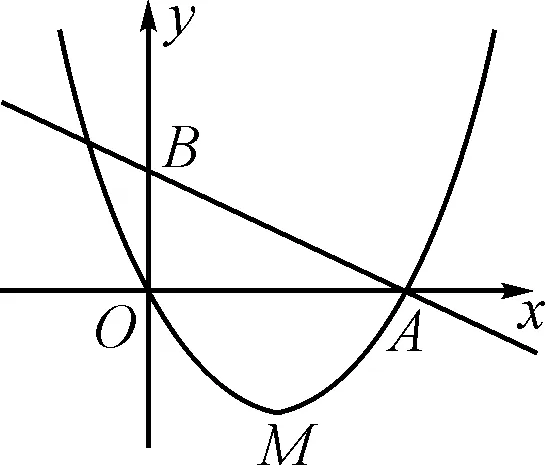
圖1
(1)求b的值及點M的坐標;
(2)將直線AB向下平移,得到過點M的直線y=mx+n,且與x軸的負半軸交于點C,取點D(2,0),連接DM,求證:∠ADM-∠ACM=45°;
(3)點E是線段AB上一個動點,點F是線段OA上一個動點,連接EF,線段EF的延長線與線段OM交于點G.當∠BEF=2∠BAO時,是否存在點E,使得3GF=4EF?若存在,請求出點E的坐標;若不存在,請說明理由.
2.2 分步突破
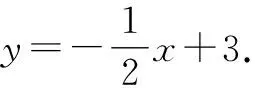
第一步——突破角度差.
第(2)問對直線AB進行了向下平移,然后設定點C,通過連線形成了幾何角∠ADM、∠ACM.基于問題構建的過程,可分兩階段來證明:第一階段,確定平移后的直線的解析式;第二階段,確定∠ADM與∠ACM的角度關系,可進行等角轉化,將角度差化為具體的角.

階段二:∠ADM可視為△CDM的一個外角,則∠ADM-∠ACM=∠DMC.只需確定∠DMC的大小即可,可將其放置在三角形中.
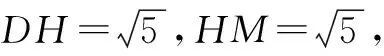
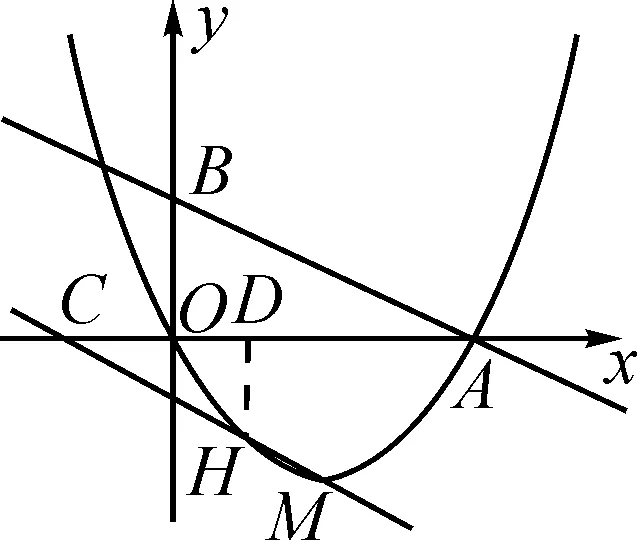
圖2
第二步——突破倍角關系.
第(3)問有兩個動點——點E和F,分析∠BEF=2∠BAO時,是否存在點E,使得3GF=4EF,可歸結為與倍角相關的線段關系存在性問題.采用假設順推的方式,第一階段處理其中的倍角關系,分析幾何性質;第二階段構建線段關系,論證點E是否存在.
階段一:假設存在點E滿足3GF=4EF.分別過點G和E作x軸的垂線,垂足分別為點H和K,如圖3所示.
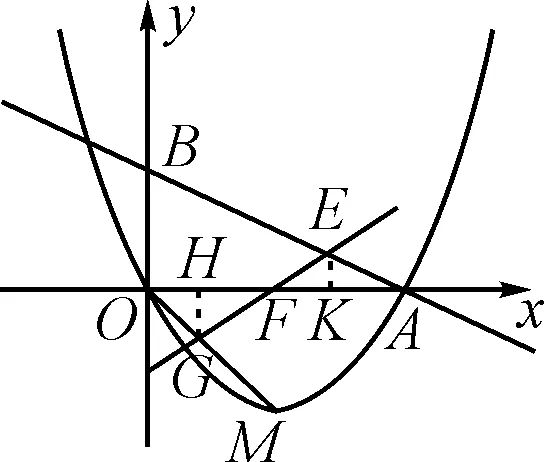
圖3
因為∠BEF=2∠BAO,由∠BEF=∠BAO+∠EFA,可得∠EFA=∠BAO,即△EFA為等腰三角形,進一步可得∠EFA=∠GFH.
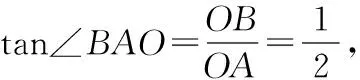
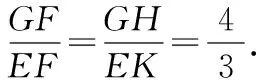
3 過程分析,方法總結
上述考題的第(2)(3)問是關于二次函數與幾何角的問題,處理其中的角度問題與條件是突破的關鍵.下面深入分析思考過程,并總結方法.
3.1 過程評析
第(2)問屬于角度和差問題.上述解析中采用等角代換的策略,將角度和差變換為具體的幾何角,后續再探究該角的大小.由于問題的條件中沒有設定具體角度,故由幾何性質來提取特殊圖形,確定特殊角.而第(3)問涉及倍角關系,充分利用了三角形的外角性質,結合倍角條件推導出了等角關系,進而提取了等腰三角形,實現了倍角條件向特殊圖形的轉化.
3.2 方法總結
上述第(2)問和第(3)問是關于角的數量關系問題,依托拋物線的同時,賦予了角度“數”的特性,這是該類問題的特殊所在.問題解析時,需要建立幾何特性與二次函數間的關聯,數形結合突破.下面總結兩大問題的解析方法.
角度和差問題:角度和差涉及角度之間的加減運算,基本策略是利用幾何性質轉化為具體的角,去除運算符號.可利用三角形內角和定理、外角定理等進行角度換算.
倍角關系問題:倍角關系問題雖引入了角度系數,但本質上還是關于角度關系的推理.可利用幾何中與倍角相關的定理,如角平分線的性質、等腰三角形性質,或構建對稱關系,引入輔助圓來分析轉化.
3.3 關聯拓展
實際上,角的數量關系問題可分為三大類,除了上述所涉及的角度和差、倍角關系問題,還有等角問題.該類問題的突破同樣需要借助特殊的幾何性質,如全等特性和相似特性,可構造圓,利用圓周角性質轉化角度關系.下面以一個實例進行探究.
例題已知拋物線y=ax2-2ax+c過點A(-1,0)和C(0,3),與x軸的另一交點為B,其頂點為D.
(1)求拋物線的解析式,以及點D的坐標.
(2)如圖4,點E是線段BC上方的拋物線上一點,且EF⊥BC,垂足為點F,EM垂直于x軸,垂足為點M,與BC的交點為G.當BG=CF時,求△EFG的面積.
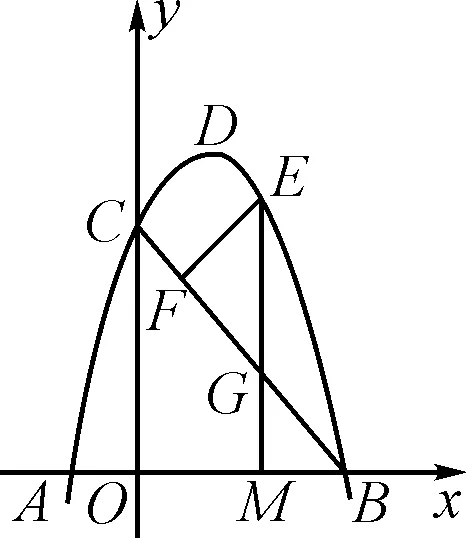
圖4
(3)如圖5,AC與BD的延長線相交于點H,分析在x軸上方的拋物線上是否存在一點P,使得∠OPB=∠AHB?若存在,請求出點P的坐標;若不存在,請說明理由.
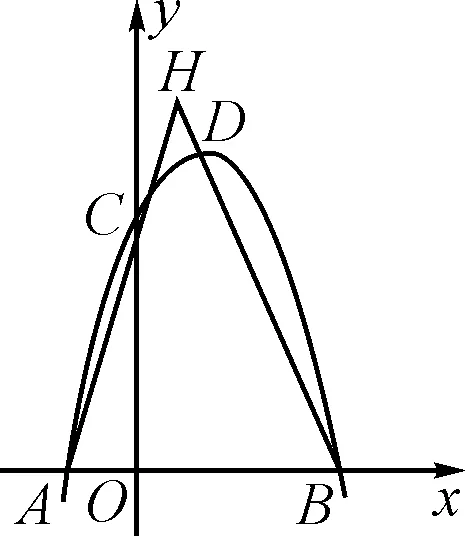
圖5
解析:第(1)(2)問解答略.下面主要探究第(3)問等角關系問題.
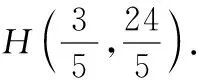
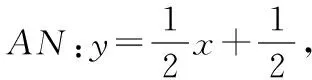
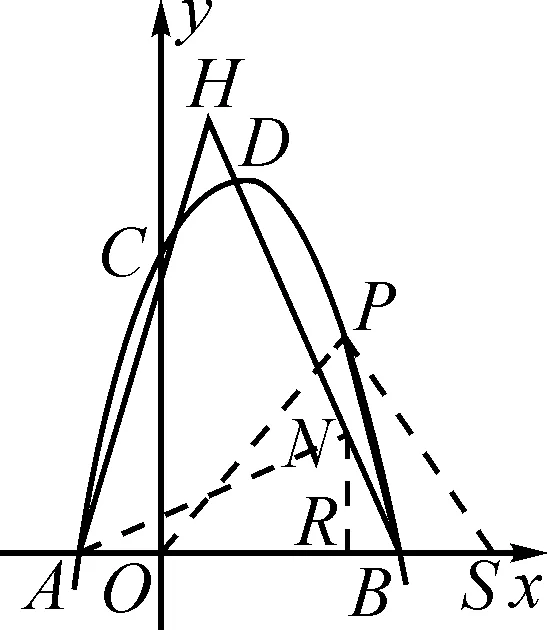
圖6
過點P作x軸的垂線,設垂足為點R.在x軸上取點S,使得RS=PR,則∠RSP=45°.設P(n,-n2+2n+3),則S(-n2+3n+3,0).
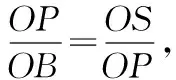

評析:上述第(3)問是關于二次函數與等角關系的問題,所涉角中其中一角為定角,可直接由幾何性質確定為特殊的45°角,后續圍繞點P構建特殊的等腰直角三角形,并借助三角形相似的性質確定動點P的位置.整個過程思路明確,按照“角度確認→圖形構造→特性定點”的思路整合信息,構形求坐標.
4 解后反思,教學建議
4.1 歸類題型,總結方法
二次函數與幾何角問題屬于初中數學重點和難點問題.根據角度條件,可將角度關系分為三類,包括等角問題、倍角問題和角度和差問題.上述結合實例對其加以探究,并總結了思路構建的基本策略,有助于學生后續突破類型問題.復習教學中,建議參考該種模式,引導學生定位問題類型,全面歸納題型,總結破題的基本策略.必要時,可開展對比探究,引導學生探究不同題型的特征、解法特點,從根本上掌握解題方法.
4.2 過程探究,思維培養
過程探究是解題教學的重要環節.過程探究中,可引導學生充分體驗讀題、審題、條件轉化、模型構建、關聯提取、思路形成、問題解答等重要過程,培養學生系統解題的良好習慣,促進數學思維的發展[1].以上述問題探究為例,確定問題屬性,根據條件及問題進行分步解題,然后構圖建模,串聯條件形成思路.教學中,需關注兩點:一是學生的思維活動,充分調動學生思考,可采用設問引導的方式;二是數形結合的過程,直觀呈現問題,降低思維的難度,培養學生的思維習慣.
4.3 滲透思想,素養提升
解題教學還需注重數學思想培養,即教學中合理滲透數學思想方法,讓學生在解題中掌握方法,感悟思想精髓,逐步提升數學素養[2].二次函數與角度類問題常涉及數形結合、化歸與轉化、方程思想、數學建模、分類討論等,教學中,可立足具體的內容開展思想方法教學,感知思想方法在解題中的具體運用.如函數與圖象內容滲透數形結合,二元一次方法組內容滲透方程思想,等等,將無形的思想滲透到具體的內容中,逐步提升學生的綜合素養.

