探討有約束條件下水平盤上物體做圓周運動的臨界條件

鄧柳詠 李廣凌

(廣東省廣州市南武中學 510220)

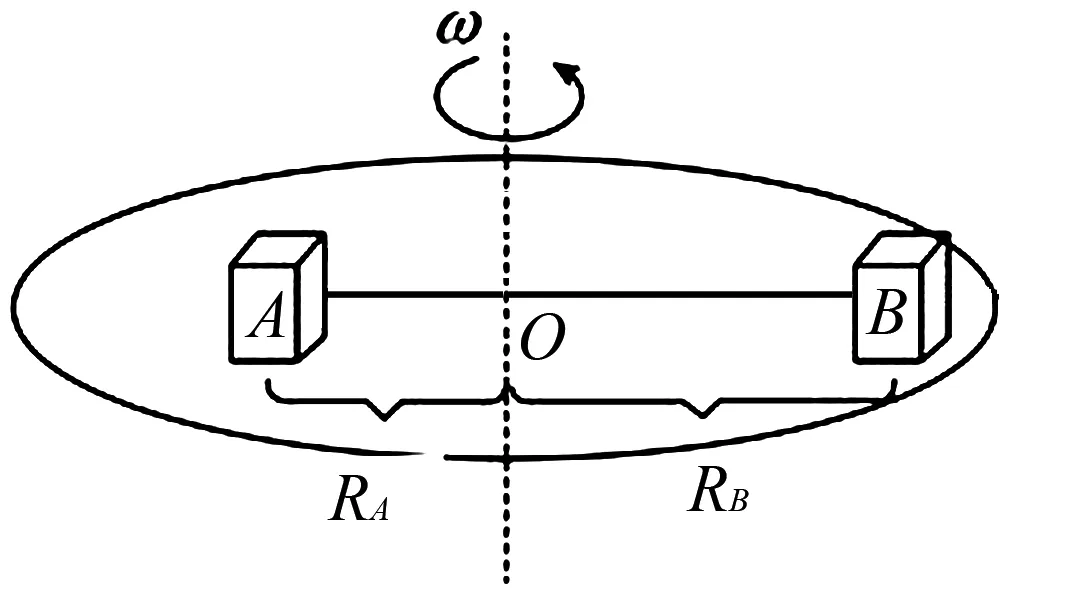
題目如圖1所示，在勻速轉動的水平盤上，沿半徑方向放著用細線相連的質量分別為mA和mB的物體A和B；它們分居圓心兩側，與圓心距離分別為RA和RB，且RA

圖1

該題目主要是考查有約束條件下勻速轉動水平盤的臨界狀態的分析，解題的關鍵是判斷發生滑動時作離心運動時的狀態，究竟是物體A離心運動，從而拉動物體B，還是物體B離心運動，從而拉動物體A.

思路分析假設兩物體剛好發生滑動時，A作離心運動，B作近心運動，列出各自的牛頓第二定律方程，聯立解出對應的角速度，并討論對應的運動狀態是否存在.

分析過程假設兩物體剛好發生滑動時，由于繩子的作用，A作離心運動，B作近心運動，A和B受到圓盤的摩擦力為滑動摩擦力,分別表示為fA=μAmAg和fB=μBmBg.對A和B受力分析，如圖2所示，應用牛頓第二定律：

圖2

T+μAmAg=mAω2RA

①

T-μBmBg=mBω2RB

②

聯立①式和②式可得到系統的臨界角速度關系式為：

μAmAg+μBmBg=(mARA-mBRB)ω2

討論：

(1)mARA-mBRB>0，則假設是成立的，得到臨界角速度大小表達式為：

③

(2)mARA-mBRB<0，則假設是不成立的，則運動狀態只能為A作近心運動，B作離心運動，根據其對應的受力分析，列出牛頓第二定律方程，如下：

T-μAmAg=mAω2RA

④

T+μBmBg=mBω2RB

⑤

聯立④式和⑤式，可得到：

⑥

討論對比③式和⑥式，可以得出下列可以直接應用的結論：

(1)系統剛好發生滑動時，物體的運動狀態由mARA-mBRB的數值決定.若mARA>mBRB，則物體A離心運動，從而拉動物體B；若mARA

應用如圖3所示，勻速轉動的水平圓盤上放有質量分別為2 kg和3 kg的小物體A、B，A、B間用細線沿半徑方向相連.它們到轉軸的距離分別為rA=0.2m、rB=0.3 m.A、B與盤面間的最大靜摩擦力均為重力的0.4倍.g取10 m/s2，現極其緩慢地增大圓盤的角速度，當兩物體剛好發生滑動時，圓盤的角速度約為____.

圖3

深入探討回歸問題可以知道，上文得到的臨界角速度的表達式屬于我們常說的“二級結論”.在應用時，“二級結論”有特定的情景要求，使得其適用性受限.為了解決適用性受限的問題，現在利用上文的提到的分析方法來分析水平盤上作圓周運動的其他種情況來來深入探討一般的分析方法.

如圖4所示，粗糙水平圓盤上，可視為質點的木塊A、B疊放在一起，放在水平轉臺上隨轉臺一起繞固定轉軸勻速轉動，A的質量為mA，B的質量為mB.已知A、B到轉動軸的距離為r，A與B間的動摩擦因數為μAB，B與轉臺間的動摩擦因數為μ，(最大靜摩擦力等于滑動摩擦力，重力加速度為g).現緩慢地增大圓盤的角速度，請分析需要什么條件才能使A與B保持相對靜止.

圖4

結合情景觀察，可能出現兩種不同的運動情景：

(1)物體A和B同時向外作離心運動.

(2)物體A作離心運動，物體B還可以跟隨圓盤作圓周運動.

分析方法隔離分析物體A和B的受力情況，假設可能存在情景(2)，列出各自的牛頓第二定律方程組，并結合情景所隱含的數量條件，解出特定的數量關系，并討論對應運動狀態是否存在.解答過程如下：

分別對物體A和B的受力分析，應用牛頓第二定律：

fAB=mAω2r

⑦

f-fAB=mBω2r

⑧