實現多元合一有效融入STEM教育理念

◇任寶生（甘肅：涇川縣玉都鎮郭馬村小學）

STEM 教育理念最早源于20世紀中期的美國，其在當時屬于科學教育領域較為先進的理念之一。近些年，STEM 教育理念傳入我國，并在原先的基礎上對其進行了一定程度的修改，最終形成了一套適合我國當前教育形勢、有著發展價值的教育理論體系，并越來越成為當前教育的主流思想。STEM 包含了科學、技術、工程、數學四個不同的領域，而且，不僅僅是對這四個領域內容的簡單概括，還將它們匯聚成了一個有機的整體，實現了真正意義上的多元合一。這一教育思維也值得廣大教育工作者在教學的其他領域中參考借鑒，以達到相同的效果。

一、貫徹STEM教育理念，突顯教學融合價值

要想在教學中有效貫徹一種新的教學理念，首先必須找準它的理論方向，其主要依據便是該理論的基本思想與主要目標。順著這些線索前進，自然能夠將其有效應用于教學實踐，充分體現其對教學的實際價值。

（一）認清規律，降低教學難度

例如在小學數學（人教版）二年級上冊第7 課《認識時間》的教學中，時間是一個相對抽象的概念，雖然時間每時每刻都在流逝，但我們無法直接觀察時間的變化。因此，教師教學時間這一概念就顯得格外困難。為了讓學生理解時間流逝的本質及其對應的速度，就引入了鐘表這一工具。學生只要觀察鐘表上數字的變化，就知道時間流逝的快慢和多少，發現時間的規律。認清時間概念之后，學生在后續的學習及練習中，也能更好地發揮，實現認識水平和學習成績的提升。

上述方式，也是對STEM 教育理念的把握，突出了規律的發現與運用對教學開展的作用。在小學數學教學中，還存在大量概念理解性內容。教師要充分利用這種思維，為學生建立知識點系統性的理論框架，幫助學生打好數學基礎。

（二）巧用多種工具，開拓教學途徑

STEM 教育理念強調，要脫離傳統教學模式的各項限制，靈活使用現代化工具，開展新時代教學。隨著時代的發展，近年來涌現出了許多新型的信息工具，如電子白板、平板電腦、學習機等。教師在教學中，要主動使用這些工具，幫助學生掌握各知識點以及數學學習和解題的高效方法。

以小學數學（人教版）三年級下冊第5 課《面積》的教學為例。在教學這節課之前，學生對面積的概念及內容所知有限。而面積問題在小學中又屬于常見但難度偏高的問題，因此，基礎對于學生而言尤為重要。面積雖然只是數據，但它不可能單獨存在，而必須依托于圖形。為此，教師在面積這一知識點的教學中，可以采用數學中的數形結合方法。以其中的一道課堂練習題為例。

例題：已知一個長方形的周長為120 厘米，長比寬要長12 厘米，問該長方形的面積為多少平方厘米？

引導：通過簡單的教學，學生已經熟知了長方形、正方形中面積與邊長之間的關系，但本題中并未直接給出這個關系表達。為了方便學生計算，避免出現錯誤，宜采用數形結合的思維方法，可以先利用電子白板或傳統的黑板工具構建一個符合題目要求的圖形。如下圖所示。

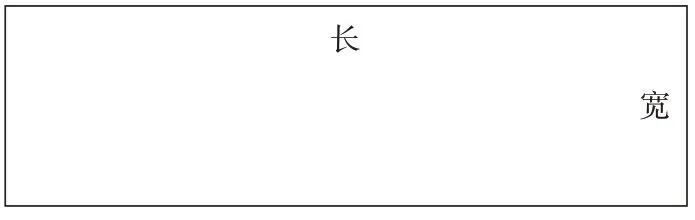
解析：由圖形及題中所給出的條件可以得知，長+寬=60 厘米，長-寬=12 厘米，由此便可以直接計算出，長方形的長為36厘米，寬為24厘米。再代入面積公式s=長×寬，得出S=864平方厘米。

（2）樣品濾筒溶液的制備［6］。將采樣后的濾筒撕碎放入250mL錐形瓶中,加100mL水浸沒,瓶口上放一玻璃漏斗于電爐或電熱板上加熱近沸,約30min后取下,冷卻后將浸出液用中速定量濾紙濾入250mL容量瓶中,用20～30mL水洗滌錐形瓶及濾筒殘渣3～4次,洗滌液并入容量瓶中,用pH試紙試驗,加1.0或0.10mol/L氫氧化鈉溶液中和至溶液pH7～9,再用水稀釋至標線。

當然，在小學數學中，還存在許多其他的數學思維及解題方法。在以往的教學中，由于條件的限制，這些方法無法得到廣泛的運用。教師必須緊跟時代的發展，在開展教學中主動引入新的工具，大膽進行嘗試，這同樣是STEM 教育理念的方向之一。

二、透析STEM教育理念，豐富教學內容

多門學科綜合，多種技術共用，促進社會全面發展，個人水平全面提升，是STEM 教學的主要策略。此策略應用在教學中，就是要采用多種方式、結合不同學科，對知識點及其所包含的例題進行講解，在豐富課堂內容的同時，強化學生的學習能力。在當前教育改革的背景下，這種教學模式有著獨特而又神奇的作用。

（一）介紹知識背景，積累學生常識

在以往的教學模式中，教師常常一開始展開教學就講解知識點或者以例題作為課堂的開頭。這樣的課堂設計雖然能在一定程度上給予學生思考聯想的空間，但也容易導致學生根基虛浮，知識點基礎知識掌握不夠。STEM 教學策略要求教師的教學從根本出發，重點鞏固學生對基礎知識及知識背景的理解。為此，教師在課堂的設計上，可以以知識點的由來或在生活中的表現為開頭。

例如在小學數學（人教版）六年級上冊第5 課《圓》的課堂教學中，教師教學的第一步就可以介紹圓這種形狀的由來及對其規律最早的發現。

在此之前，許多學生對圓往往會有這樣的想法：“圓只是人們想象出來的圖形，跟三角形、長方形等類似，都是由巧合情況被人所發現的。”人們接觸到的最早的“圓”是太陽與月亮，在人的視角中，這兩個天體呈現的形狀就是標準的圓形。其實，早在數千年前，古人就已經能利用“圓”完成一些生活活動。例如陶器時代人們制作的陶器中，底邊或開口有很大一部分就是呈圓形的；在春秋戰國時期，搬運糧草或作戰時使用的馬車，其車輪同樣也是圓形的。直到兩千多年前，墨子提出了“圓”“一中同長”的概念模型，人們才對“圓”有了相對完整的認識。這一模型也為后世圓面積與周長的計算，提供了指引，也就是“圓”在教材中的知識內容。

對圓的由來及發展的具體講述，既豐富了課堂氛圍，提升了學生學習的興趣，也強化了學生對知識的理解。從本質出發，更激起了學生探索生活中事物的渴望，為學生建立了像古人一般敢于探索、敢于發現的理念。這種理念正是社會所需要的，在此指引下，一些當前存在的問題，能夠得到有效解決，社會發展的速度也能得到一定提升，這對應著STEM教育理念中人類社會持續發展的目標。

（二）引入視頻資料，啟發學生思路

隨著信息化時代的持續發展，從網絡中搜集資料已經不再困難。尤其是在教育領域中，有著大量的相關視頻，值得教師在課堂中借鑒引用，以豐富課堂的內容。教師在選取視頻資料的時候，可以重點關注這幾類內容：科普類視頻、高效數學方法講解類視頻以及名校名師講堂等。在課堂中，播放這些優質視頻，不僅能提升學生的學習興趣，還能啟發其思維，引導學生自主學習。

以小學數學（人教版）四年級下冊第9 課《數學廣角——雞兔同籠》的教學為例。雞兔同籠問題在小學中屬于難度相對較高、需有一定推理能力才能解決的問題。同時，該問題解法多樣，不同的解法步驟過程也不相同。然而，一種解法并不一定適用于所有學生，掌握多種解法也能在很大程度上啟發學生的思維。為此，教師可以引入視頻《雞兔同籠問題解法集合》，讓學生了解不同的解法，并選擇其中一種或多種加以應用。例如在課堂中有這樣一道例題：

雞兔同籠，有頭40 個，足116 只，問有雞、兔各多少只？

針對這一問題，視頻《雞兔同籠解法集合》中給出了四種具體的解題方法，這里介紹其中的兩種。

解法一：假設法，假設籠子里全為雞。首先，學生必須清楚，題中給出的數據，頭的數量實際上就是動物的數量。雞、兔在本題中唯一的區別就是雞只有兩只足，而兔有四只。因此，當籠中全為雞時，足的數量應該是40×2=80 只，而實際結果是116只，相差116-80=36 只。由于兔的足數比雞多兩只，因此可以得出兔的數量為36÷2=18只，雞的數量為40-18=22只。

解法二：公式法，經過眾多教師多年的經驗綜合，對雞兔同籠問題建立了一套完整的公式體系，只要套用公式，便能有效解決問題。其公式為：總足數÷2-總頭數=兔的數量，總頭數-兔的數量=雞的數量。代入題中就是：兔的數量=116÷2-40=18 只，雞的數量=40-18=22 只。這種方法能較快解出答案，但存在一定的局限性，應對靈活的題目，則常常表現得束手無策。因此，該方法僅作為學生在沒有思路時，備用的解題方案。

通過一個視頻，學生認識了解決一類問題的多種方式，有基礎認識部分，也有擴展提升部分。將此類視頻引入課堂，既能豐富課堂內容，提升教學效率，也能適應不同學習情況學生發展的需要，符合STEM教育理念的策略要求。

三、應用STEM教育理念，激發學生潛能

STEM 教育理念的優勢在于其靈活性與綜合適應性，能夠有效整合多種不同方向的內容，形成一個有機的整體。這種教育方式，對學生潛能的激發也能起到重要作用。

（一）學科串聯，強化學生整合意識

學科的跨越性串聯是STEM 教育理念的核心部分，該部分在小學數學中的集中表現是“將小學科學技術學習與數學學習之間相互關聯”。科學技術與數學之間本就有著多重聯系，科學的學習也必須建立在一定的數學基礎之上。為此，教師能夠較容易地將兩者知識點結合進行講解。

例如可以將小學數學（人教版）三年級上冊第3課《測量》課堂教學與小學科學（人教版）第一冊第四章第三節《尺的使用》進行串聯整合。尺子是小學生測量物體的常用工具，而許多學生對于“尺”的規范使用并不清楚。而在小學科學的學習中，學生清楚了尺子在測量物體時的規范用法。以測量正方體的邊長為例（如圖所示），首先必須對齊零刻度線，其次在測量中，要使尺子與待測的面垂直，最后測出實際數值，并進行估讀。以本次測量數值為例，正確的讀數應為10.1毫米。

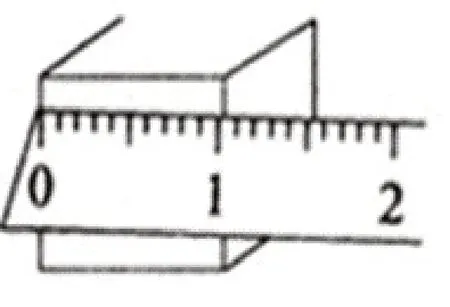
由此可見，學科的串聯性對于教學的開展具有重要意義，其不僅能提升教學質效，還能建立一個良性的教學模式，幫助學生鞏固所學知識內容，提升思維路徑。

（二）齊頭并進，促進學生全面發展

STEM 教育理念對學生的全面發展提出了很高的期望，希望學生能夠借助STEM 教育的特殊模式，發揮長處，補齊短板，促進自身的全面發展。為此，在該理念的引導下，教師要著重關注學生在當前學習中存在的問題，及時進行糾正。

教學并不是單方向一味前進的過程，教師在開展教學時，也必須注意實時回顧。要以學生的學習情況為基礎，做到齊頭并進，使學生的學習成績與認識水平穩步提升，滿足STEM 教育理念在教育實踐中的需要。

綜上所述，STEM 教育理念作為教育體系改革下教學發展的主流思想，發揮著獨到的作用。實施STEM 模式的教學，也是教育發展的必然趨勢，教師要積極響應，主動接受。