“二次函數圖象與性質”教學設計與反思
——核心素養視角下數學復習課的實踐研究

林佳娜

(廣東省廣州市第九十七中學，510000)

筆者在廣州市的教研活動中開了一節公開課,課題是“二次函數的圖象與性質”,教學設計的核心環節是以下的開放性問題.下面對課堂的主要環節進行回顧與反思.

一、課堂核心部分回放

(一)開放性問題——基本圖形我來讀

二次函數y=ax2+bx+c的部分圖象如圖1所示,當x取一切實數時,請將圖象補充完整,寫出三個以上的正確結論并說明理由.

這是一個開放性問題，需要留給學生充分的思考時間.

設計意圖通過相關結論的挖掘,旨在幫助學生對二次函數核心知識進行重點回顧．

(二)問題回想—數學味道我來品

1.方法解讀—如何識圖(腳手架)

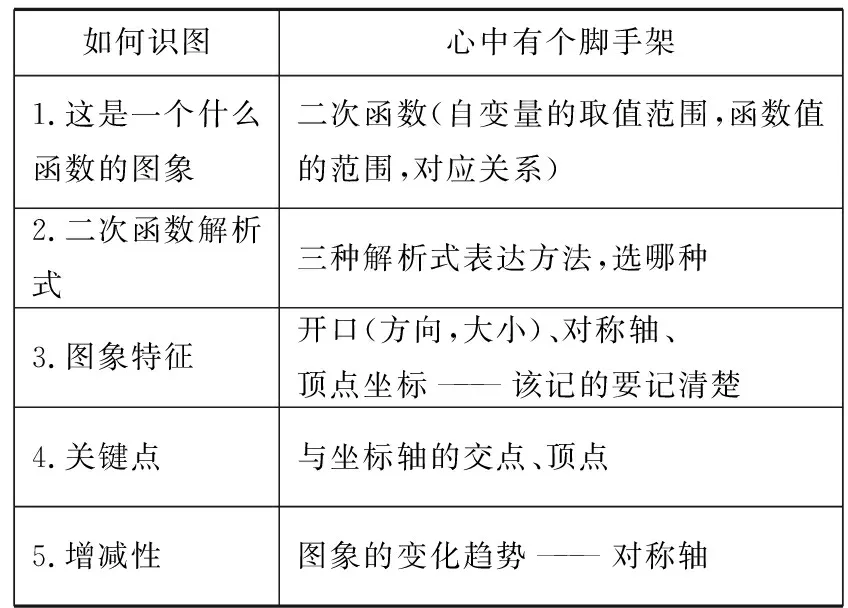
如何識圖心中有個腳手架 1.這是一個什么函數的圖象二次函數(自變量的取值范圍,函數值的范圍,對應關系) 2.二次函數解析式三種解析式表達方法,選哪種 3.圖象特征開口(方向,大小)、對稱軸、頂點坐標———該記的要記清楚 4.關鍵點與坐標軸的交點、頂點 5.增減性圖象的變化趨勢———對稱軸

2.欣賞你的結論——由小見大,建構我的數學王國形(一個小小的圖象)——數(一串長長的結論)表面的——深層的(多看多想).

(三) 問題延伸——題目我來編

在寫結論過程中,你認為哪個條件最重要,想不想改變一下?編個題目來試試.

設計意圖編題過程是課堂學習變式訓練的延續.

二、復習課教學與反思

(一)備課反思—教學目標定位

首先,復習的目的是什么?其次,一節課時間就40分鐘,能突破什么?這也是需要教師認真思考的.

本節課的教學目標:

1.復習二次函數圖象與性質的基礎知識(解析式、頂點坐標、對稱軸、增減性).

2.讓學生經歷讀圖過程,學會多維度地識圖讀圖,學習一般的提取圖象信息的方法，學會對獲得的信息進行歸類,并納入知識框架體系.

3.感受數形結合、轉化思想在問題解決中的應用.

(二)目標達成的方法

1.找好問題

“自學·議論·引導”教學法告訴我們,好的“問題”要具有“數學味”;好的“問題”應盡量串聯整節課.一個好問題,既能使課堂連接自然流暢，又能促進課堂的自然生成．實踐證明,“好的問題”可以給學生節省很多寶貴的時間,還能避免學生掉進“題海”.

2.深入研究好問題

本節課有機會在課堂上生成下面這樣的表格,教師一定要用好這樣的資源.本節課教師呈現出研究函數的三個層面“形—數—結合點”流暢自然.

形數結合點圖象與x軸有兩個交點b2-4ac>0方程ax2+bx+c=0有兩個不相等的實數根與x軸兩個交點是(-1,0),(3,0);與y軸交點(0,3).方程-x2+2x+3=0有兩個不相等的實數根,它們是x1=-1,x2=3,x1+x2=2,x1x2=-3y=0時,y=ax2+bx+c變成方程ax2+bx+c=0,x1+x2=-ba,而對稱軸x=-b2a頂點坐標(1,4)方程ax2+bx+c=4有唯一解x=1,方程ax2+bx+c=5無解當m取何值,方程ax2+bx+c=m有解

仔細體會一下,這里

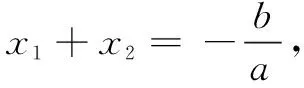
另一個過程:

x=1時,圖象上對應點最高頂點坐標為(1,4),對稱軸x=1?2a+b=0x=1時,a+b+c=4若x=m≠1,則a+b+c>am2+bm+c

對函數最高點的三個層次的理解,特別第三層，與方程自然聯系滲透,難點消逝于無形.

3.課堂的主體是學生

要弄懂問題,學生可以依靠各種方法,如，自主發現、同伴交流、教師引導,最終都要落實到自己真正弄清楚、最好是能給同伴講出來．筆者帶的這個班，一直是在李庚南老師“自學·議論·引導”教學法指導下開展教學.學生很享受這種“有規則的自由”課堂.教師的課堂問題也基本是因學生而產生的.“一個問題,一串知識”或者“一串問題,一個知識”的問題模式,是課堂教學的常態,卻讓學生常常陶醉其中．

除了課堂上的學習,學生也有做數學筆記的習慣,還可能會整理學習的點點滴滴、及時地做錯題分析和知識歸納.

4.課堂教學的引領者是老師

復習課最終是要教會學生思考:如何從表面的看到深層的(整體把握—局部突破—尋找聯系).如何把雜亂變成有序(形—數—數形結合的結合點).

學生從零散地知道有這些知識,到有序地把它們納入知識體系,再到建構自己的認知框架,都需要方法的引領.讓他們平時養成了習慣,數學思維方法慢慢就自然形成．

(1)看整體

(2)讀細節

拋物線與y軸的交點c在x軸上方c>0,c=3當x=0時,y=c.c決定圖象與y軸交點的位置圖象過點(-1,0)a-b+c=0(a+c=b)當x=-1時,y=a-b+c圖象必過點(3,0)9a+3b+c=0當x=3時,y=9a+3b+cx=1時,圖象對應點最高頂點坐標(1,4),2a+b=0.若m≠1,則a+b+c>am2+bm+cx=1時,a+b+c=4對稱軸:x=-b2a=1頂點:-b2a,4ac-b24a 圖象有在x軸上方的當-10任意舉例子:如x=1時,y>0,即:a+b+c>0圖象也有在x軸下方的當x<-1或x>3時,y<0x=4時,y<0,即:16a+4b+c<0等等圖象有對稱性y=3時,x=0或x=2(0,3)關于x=1的對稱點(2,3)圖象有增減性x<1時,y隨x的增大而增大,x>1時,y隨x的增大而減小圖象的增減性由開口方向和對稱軸共同決定

5.適時生成探索性問題

本節課的圖象問題探索過后,有沒有后續的探究問題？答案是肯定的,題目3個關鍵條件只要有一個變動,問題就動起來了.這種充滿研究魅力的問題,師生當然不能錯過.

引導學生思考:(1)對稱軸變為x=n,其他條件不變,我們來研究研究.

從數的角度解釋—用數式的方式,你怎么做?

y=a(x-n)2+k，過點(-1，0)，(0，3).

從a的表達式,你得到什么?何時開口向上?向下?

(2)若對稱軸變為x=n,且n>0，其他條件不變,你能分析啊a+b+c的取值范圍嗎?

(三)課堂整體表現

在寫結論環節,全班每一個學生的筆都動了起來.從獨立探索結論,到后面的小組交流、歸納匯總、教師在整堂課上并沒有叫學生解哪一道具體的題目.但一節課下來,學生經歷了圖象提取信息、解讀信息、分類匯總的過程,他們已經做了不少題.學生身心愉悅,以非常積極的狀態投入到了學習中來,這是教師所樂于見到的.這也從另一個角度告訴我們,學生是充滿學習智慧的,等待良師用心去栽培.