關(guān)于教材中一道課后習(xí)題的思考

哈爾濱市第一〇七中學(xué) 唐 宏

人教版義務(wù)教育課程標(biāo)準(zhǔn)實(shí)驗(yàn)教科書數(shù)學(xué)八年級（下冊）第二十五章中有這樣一道很值得回味的課后習(xí)題。原題：如圖，四邊形ABCD是正方形，點(diǎn)E是BC邊的中點(diǎn)，∠AEF=90°，且EF交正方形外角的平分線CF于點(diǎn)F，求證：AE=EF.（提示：取AB的中點(diǎn)G，連接EG.）

一、問題的分析

這道課后習(xí)題是一道非常值得研究的好題，深入研究這個問題能夠把初中直線型幾何問題發(fā)揮得淋漓盡致。教材中的處理大大降低了這道題的難度。第一，教材中給了解決問題的提示，學(xué)生根據(jù)提示很容易構(gòu)造兩個全等的三角形，從而順利地得到結(jié)論。第二，題目中把點(diǎn)E設(shè)置為BC邊中點(diǎn)，使問題特殊化，在問題的解決上可能就會用到特殊的方法，如利用計算也可以解決這個問題。

我們發(fā)現(xiàn)點(diǎn)E在直線BC上任意位置結(jié)論都成立，也就是說這道題并不是靜態(tài)的數(shù)學(xué)問題，而是一個動態(tài)問題，我們在教學(xué)時，可以適當(dāng)調(diào)整，如將點(diǎn)E是BC中點(diǎn)改為點(diǎn)E是BC邊上一點(diǎn)，對于知識點(diǎn)掌握好的學(xué)生，可以考慮點(diǎn)E為直線BC上一點(diǎn)，分情況探究。或是去掉提示，讓學(xué)生的思想從束縛中解放出來，充分想象在初中階段證明兩線段相等的方法有哪些，根據(jù)這些思維想象，設(shè)計解決問題的方法，最后達(dá)到解決問題的目的。

在幾何證明問題中，最常見的就是證明線段相等或角相等，其方法也是多種多樣，這里我們以線段相等為例，研究證明兩條線段相等的一些主要思想與方法。

二、問題的提出與解決

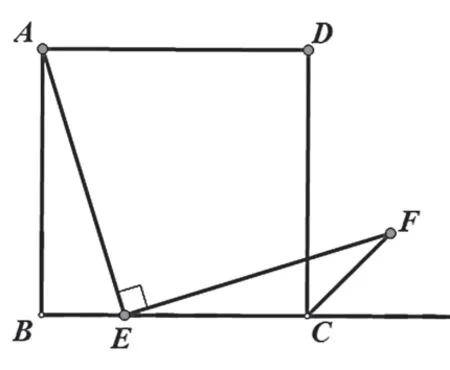
例題：如圖，四邊形ABCD是正方形，點(diǎn)E是BC邊上一點(diǎn)，∠AEF=90，且EF交正方形外角的平分線CF于點(diǎn)F.求證：EF=AE.

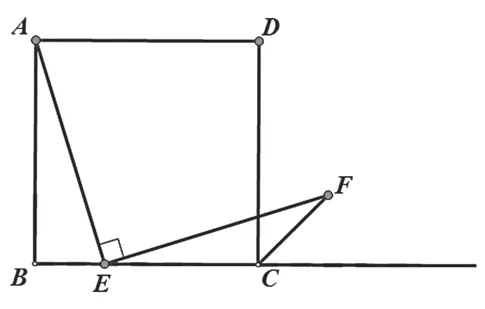
分析角度一：邊等角等構(gòu)全等

本題中證明線段EF=AE，可以考慮把線段EF、AE放在兩個三角形中證全等，但是EF與AE所在的兩個三角形不全等，因此可以考慮構(gòu)造全等三角形。

因?yàn)椤螩EF=∠BAE，EF=AE，但CE≠AB，可以考慮構(gòu)全等三角形。

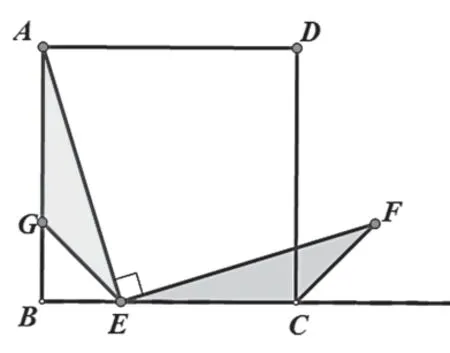
解法1：

在AB上截取AG=EC，

證明△CEF≌△GAE，所以EF=AE.

小結(jié)：利用已知條件一組對應(yīng)角等，截取邊相等構(gòu)造全等三角形。

連接AC可證∠CFE=∠CAE，EF=AE，但CF≠AC，可以考慮構(gòu)全等三角形。

解法2：保留△CEF，

連接AC，因正方形ABCD，

過點(diǎn)E作EG⊥BC，交AC于G，則∠EGC=∠ECG=45°，

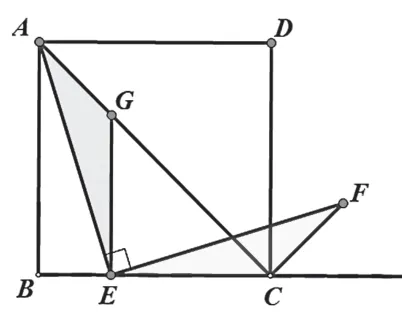
證明△ECF≌△EGA，所以EF=AE.

小結(jié)：利用正方形對角線的性質(zhì)，連接對角線，得到角相等，構(gòu)造全等三角形。

解法3：保留△ACE，

連接AC，因?yàn)檎叫蜛BCD，

過點(diǎn)E作EG⊥BC，交FC延長線于G，

證明△AEC≌△FEG，

所以EF=AE.

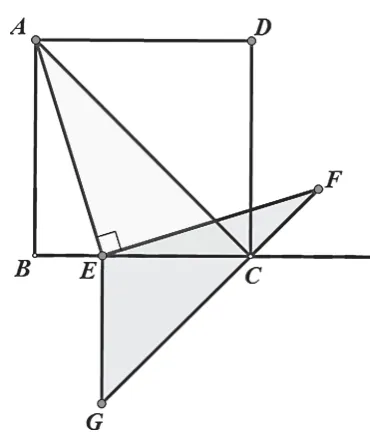
小結(jié)：利用正方形對角線的性質(zhì)，連接對角線，利用翻折構(gòu)造全等三角形。

分析角度二：從圖形變換看

本題證明線段EF=AE，可以通過圖形變換改變AE或EF的位置，再證明相等，也就是等量代換。

通過對△ABE實(shí)施變換來改變AE的位置得到新的線段，證明變換后的線段等于EF。

解法4：對△ABE作翻折變換，

延長FC交AB的延長線于G，

證明△GBE≌△ABE，

所以∠BGE=∠BAE，EG=AE，

因?yàn)椤螩EF+∠AEB=90°，∠-GAE+∠AEB=90°，

所以∠CEF=∠BAE=∠BGE，

因?yàn)椤螮GF+∠BGE=45°，∠EFG+∠CEF=45°，

所以∠EGF=∠EFG，

所以EF=EG，所以EF=AE.

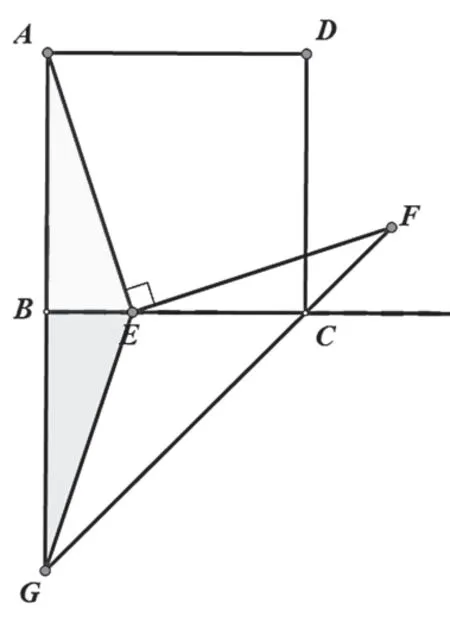
小結(jié)：利用等量代換，根據(jù)翻折變換把相應(yīng)線段進(jìn)行轉(zhuǎn)換。

解法5：對△ABE作旋轉(zhuǎn)變換

因?yàn)檎叫蜛BCD，

在AB的延長線上截取BG=BE，連接EG

證明△ABE≌△CBG，

所以AE=CG，∠ECG=∠BAE=∠CEF，

所以EF//CG，所以四邊形EGCF是平行四邊形，

所以EF=CG，所以EF=AE.

小結(jié)：利用等量代換，根據(jù)旋轉(zhuǎn)變換把相應(yīng)線段進(jìn)行轉(zhuǎn)換。

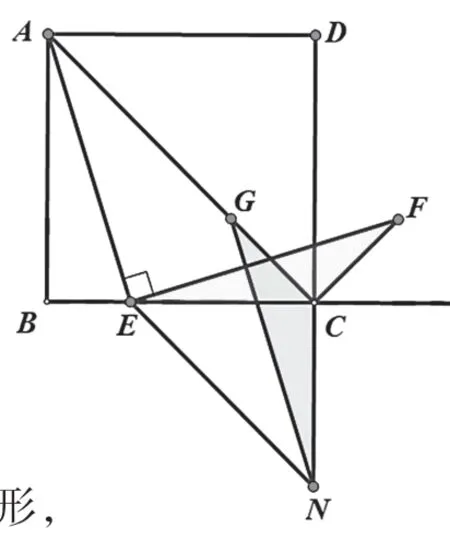
解法6：對△CEF作旋轉(zhuǎn)變換

連接AC，因?yàn)檎叫蜛BCD，

在AC上截取CG=CF，

在DC的延長線上截取CN=CE，連接NG、NE，

證明△ECF≌△NCG，

證明四邊形AENG為平行四邊形，

所以NG=AE，所以EF=AE.

小結(jié)：利用等量代換，根據(jù)旋轉(zhuǎn)變換把相應(yīng)線段進(jìn)行轉(zhuǎn)換。

三、問題的變式訓(xùn)練

（一）題目中的條件結(jié)論互換

變式一：如圖，四邊形ABCD是正方形，點(diǎn)E是BC邊上一點(diǎn)，G在BC的延長線上，F(xiàn)在∠DCG的平分線上，且EF=AE.

求證：EF⊥AE.

變式中把原題的已知和結(jié)論進(jìn)行了互換。

解法1：翻折△ACE

延長FC到N，使CN=CA，連接EN，

可證△NCE≌△ACE，

所以∠N=∠CAE，NE=AE，

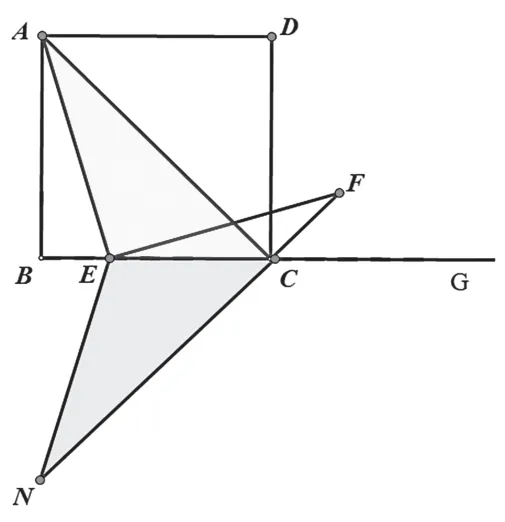
又 因 為EF=AE， 所 以EF=NE，

所以∠N=∠F，所以∠CAE=∠F，

所以∠AEF=90°，即EF⊥AE.

解法2：翻折△ECF

延長AC到N，使CN=CF，連接EN，

由∠FCE=∠NCE=135°，EC=EC，

則可證△NCE≌△FCE，

所以∠N=∠F，EN=EF，

又EF=AE，所以EN=AE，

所以∠N=∠CAE，所以∠CAE=∠F，

所以∠AEF=90°，即EF⊥AE.

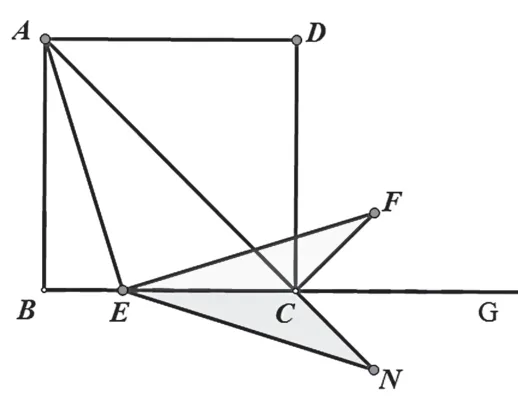
解法3：做雙垂構(gòu)旋轉(zhuǎn)

過點(diǎn)E分別向AC、FC引垂線，垂足為M、N，

易證EM=EN，又AE=EF，

所以△AEM≌△FEN，

所以∠F=∠EAM，

所以∠AEF=90°，即EF⊥AE.

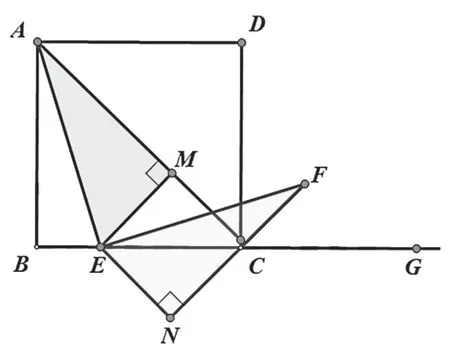
小結(jié)：有了上述證明方法，雖然條件和結(jié)論互換，仍然很容易想到解決問題的方法。考察了學(xué)生們舉一反三的數(shù)學(xué)思維。

（二）條件改為其他等價條件

變式二：如圖，四邊形ABCD是正方形，點(diǎn)E是BC邊上一點(diǎn)，G在BC的延長線上，F(xiàn)在∠DCG的平分線上，且∠EAF=45°.

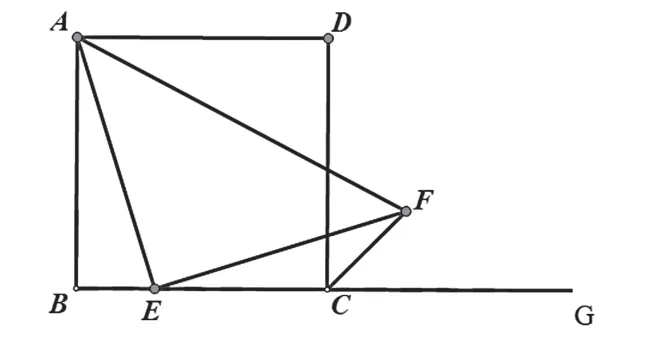
提示：此問題的主要解法是利用旋轉(zhuǎn)相似，利用旋轉(zhuǎn)相似的成對性解決問題，如下圖所示.

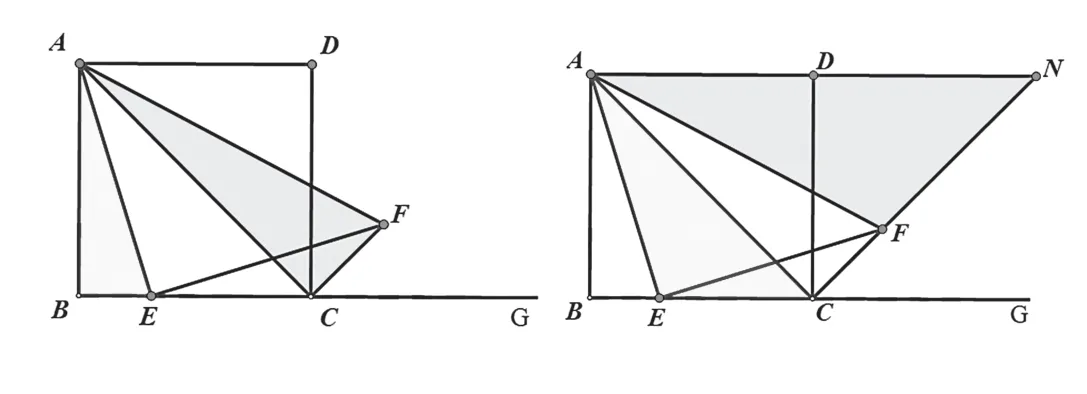
原題是教材八年級下冊的一道課后習(xí)題，教師在講九年級下冊三角形相似時，也可以把這個問題提出來，讓學(xué)生們思考能不能用相似的知識去解決。學(xué)生們會想起自己曾經(jīng)研究過這個問題，并躍躍欲試地要進(jìn)行證明。這時候教師應(yīng)該溫馨提醒：一是注意題目中條件的變化，二是應(yīng)用三角形相似的知識去解決，由此燃起學(xué)生們的學(xué)習(xí)激情。學(xué)生們思考過后，能想出用旋轉(zhuǎn)相似解決問題，既用到了圖形變換中的相似，又用到了三角形的相似，可以說是一箭雙雕。

（三）題目中的E點(diǎn)位置改為在直線BC上

變式三：如圖，四邊形ABCD是正方形，點(diǎn)E是直線BC上一點(diǎn)，∠AEF=90°，且EF交正方形外角的平分線CF于點(diǎn)F.

求證：EF=AE.

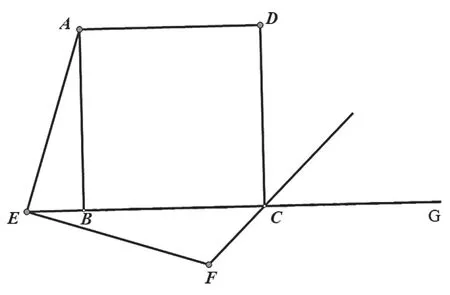
此題證明方法與前面例題方法一致。對于這個問題的變式可以留在習(xí)題課上進(jìn)行講解，等學(xué)生完全掌握了翻折、旋轉(zhuǎn)等圖形變換以后，再進(jìn)行訓(xùn)練，層層深入地把圖形變換的思想傳授給學(xué)生，讓他們的能力有一個提升。除此以外，教師還可以進(jìn)一步做研究，通過加上線段的長度，把問題綜合化，這樣也更加訓(xùn)練了學(xué)生們的思維。

數(shù)學(xué)題是做不完的，在“雙減”的大環(huán)境里，教師應(yīng)該多進(jìn)行思考，如何在有限的時間里教給學(xué)生們無限的方法，同時培養(yǎng)學(xué)生們的數(shù)學(xué)思維。數(shù)學(xué)課堂教學(xué)要在發(fā)展學(xué)生的思維能力，拓展學(xué)生的思維寬度上下功夫。一題多解與問題的變式可以很好地解決這個問題，既培養(yǎng)了學(xué)生分析問題的能力，也提升了學(xué)生解決問題的能力。將數(shù)學(xué)問題適當(dāng)變換條件或者結(jié)論，變化形式或內(nèi)容，會得到一些新的數(shù)學(xué)題。把一道數(shù)學(xué)題變成新的數(shù)學(xué)題，所用知識，解題方法都可能發(fā)生變化。通過比較鑒別，會使學(xué)生進(jìn)一步開闊思路，學(xué)得靈活；同時有利于鞏固基礎(chǔ)知識和基本技能的訓(xùn)練，起到舉一反三的作用。

問題的變式在新課、復(fù)習(xí)課和習(xí)題課都可以應(yīng)用。教師可以引導(dǎo)學(xué)生從多個角度去分析，讓學(xué)生們掌握多種方法去解決，同時體會圖形變化帶來的知識內(nèi)容上的豐盈；讓學(xué)生們自己發(fā)現(xiàn)數(shù)學(xué)知識是相通的，在學(xué)習(xí)的過程中慢慢達(dá)到預(yù)期的學(xué)習(xí)目標(biāo)。

通過這個問題的變式與拓展，希望教師在數(shù)學(xué)教學(xué)的課堂中都能重視變式的應(yīng)用，利用變式給學(xué)生們創(chuàng)造良好的思考氛圍和條件，努力達(dá)到學(xué)生數(shù)學(xué)核心素養(yǎng)落地的目標(biāo)。