小學數學學生提問“三定”教學策略研究

［摘要］ 發現問題與提出問題的能力是數學教學的重要目標。但在實際教學中，學生發現問題與提出問題的能力偏薄弱，存在多方面的原因阻礙學生數學提問思維的發展，為此，采取定學、定點、定向的方式進行探究與實踐，即確定學生的認知起點與需求、確定問題的探究設計點，以及確定提問形式與環節的方向，促使學生自信、順利地表達出疑惑與問題，有效提升學生的數學提問思維。

［關鍵詞］ 定學；定點；定向；學生提問；教學策略

筆者通過日常教學的觀察與實踐，發現學生數學的提問意識不強，導致數學課堂長期以“師問生答”的模式進行展開，使得學生的數學思維難以得到有效提升。究其問題主要有三：問題一，教學觀念轉變大，部分教師不知道“什么樣”的問題適合學生；問題二，課堂教學調控難，部分教師不知道“在哪里”設置提問環節給學生；問題三：學生負面心理重，部分教師不知道“怎么樣”激發學生提問。為改變以上現狀，促使學生自信、順利地表達出疑惑與問題，有效增進學生的數學提問思維，筆者采取“定學·定點·定向”的教學模式進行探究，即確定學生的認知起點與需求、確定問題的探究設計點、確定提問形式與環節的方向。

一、定學：把握學生“真問題”

傳統“師問生答”的教學模式中課堂問題由任課教師提出，學生只能被動聽與機械學。而“生問課堂”則將原本由教師提出的問題代之以學生說出，在教學中真正體現“四能”，這是教學觀念上的巨大轉變。學生問題指的是學生在學習推進的過程中真實產生的問題，即“真問題”，教師通過關注學生的學情與教學資料等確定學生的認知起點與需求。

（一）前測調查，尋找問題

前測是了解學生學情的重要方式，如調查問卷、訪談交流等。借助收集到的數據信息進行整理與分析，找出學生的共性問題，對學生的問題進行把脈。在教學“負數的認識”前，筆者進行了問卷調查（如下表）：

“負數的認識”調查問卷

題目1：你能寫幾個負數嗎？

題目2：你能用畫圖的方式表示出心目中的負數嗎？

題目3：你覺得0是正數還是負數？（寫一寫你的理由）

題目4：老師把小明的身高記為-3 cm，你覺得可能嗎？（寫一寫你的理由）

題目5：你對“負數”有什么疑問嗎？

對學生的提問大致總結如下：52.5%的學生提到了負數意義的問題；45%的學生提到了負數作用的問題；37.5%的學生提到了負數計算的問題；22.5%的學生提到了負數讀寫的問題；10%的學生提到了負數是怎么來的問題。這些問題在以往的教學中基本由老師拋出讓學生研究。但通過問卷調查，可以看出學生提問的欲望還是比較強烈的，對于“負數的認識”這節課還是有許多問題想要了解，其中很多就是本節課的教學重難點；還有教學外的知識，從側面說明了學生思維的發散性，這樣的問題也是教學中所需要的。

（二）全面分析，梳理問題

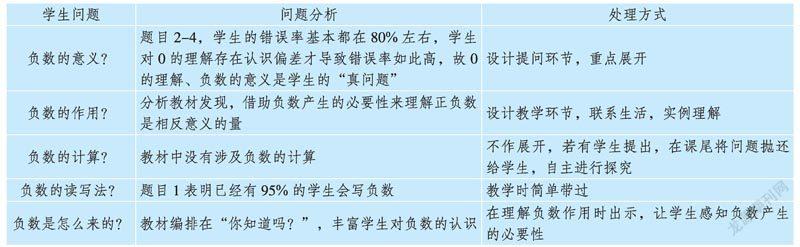
通過前測，教師把握了學生想了解、感興趣的問題，若把這些問題都放在課堂中處理，課堂時間不夠，所以我們還是要深入分析哪些“問題”真與好、哪些“問題”假與一般，這樣課堂提問的開展才能直擊學生的學習疑惑。在梳理的過程中，可以借助教學資料對學生的數學問題進行全面分析（如下表）：

借助前測與教學資料有效地幫教師梳理出學生的真問題，這些問題就是“生問課堂”推進的關鍵。在設計教學環節時，教師可以巧妙地將這三個問題轉變為學生學習中的疑惑點，再由學生自主、積極地表達出來，最后全班一起進行探究解答。

二、定點：設計提問“好時機”

好的教育一定是慢的。在開展學生提問時，教師不著急讓學生將問題提出來，而是借助手勢、言語引導學生進行觀察、思考，真正明白自己的疑惑再表達，這時提出來的問題就是學生的真問題。若學生提不出問題，教師可以自己提出，這也是一種提問技巧。設計好提問時機，對學生提問點的確定與開展至關重要。

（一）提問于探究深入點

學生學習一定的知識之后，會初步產生對此知識的理解，學生思維就會順著這種理解開始發生，形成表層的思維認知。再接著往下探究，學生可能就會產生新的問題，這時教師要做的就是等一等，讓學生梳理學習的知識要點。

如在教學“數與形”時，學生通過觀察發現從1加到n的所有奇數的和是n的平方。這時，教師拋出提問：現在你有什么新的問題想研究嗎？學生產生的問題：所有的偶數相加的和會是多少呢？所有整數相加的和會是多少呢？如果第一次是2個小正方形組成的長方形再去組成大正方形會有規律嗎？如果不是從1開始的所有奇數的和又會是怎么樣的，比如從49開始？等等。這些問題就是放緩了教學節奏后，學生自主產生的、想探究的真問題，體現著學生思考問題的全面性。如“所有的偶數相加的和會是多少呢？”若不給學生提問的機會，這個問題由教師拋出，過程中少了學生思維痕跡，學生的學習處于一種相對被動的狀態。故筆者通過“記錄—觀察—引問”，促使學生真正思考知識，自主提出這一問題，也為接下去學習起到推進的作用。

（二）提問于思維疑惑點

學起于思，思源于疑。在學生學習過程中，疑惑不可避免，這也是教師希望看到的。那如何運用好學生的疑惑，讓學生自然地消除疑惑？提問就是一種很好的方式。通過學生的表達啟發學習思考，引導學生經歷“生疑—探疑—答疑”的過程，培養學生的數學“四能”。

學生的疑惑可能出現在課前，可能在課堂推進過程中，還可能在課尾，故需要教師對學生學情有很好的把握，才能在教學時設計好提問環節，做到有條不紊。如在教學“圓的周長”時，筆者設計了如下環節：

任務單：探究圓的周長與直徑的關系

師：在數學上，圓的周長與直徑是π倍的關系，一種固定的關系。

生1：老師，為什么我們算出來的都不一樣？

生2：π是什么？

生3：那應該怎么測量才能準確得到π呢？

生4：是不是只有圓才有這種關系？

生5：圓的面積與直徑是否也是π倍的關系？

（師總結，直接解決簡單的問題，記錄推進性的問題）

課堂上，探討圓的周長與直徑的關系時，學生產生不同的結果與想法，這正是學生的思維疑惑點。教師應借助學生的自主探究與觀察討論，讓學生將疑惑表達出來。在介紹π時，先讓學生說一說對π的認識，再補充π的歷史，通過比較與感悟，真正理解π的意義與作用，強化學生知識學習的深刻性，真正消除思維疑惑。

三、定向：創建提問“多角度”

學生提問是對傳統“師問生答”觀念一種新的轉變與創新，將提問機會還給學生，讓學生形成有問題就表達、思考與解決的意識。在此過程中，教師需要確定提問形式與環節的方向，通過不斷優化設計提問環節，增強學生提問的信心；不斷給予提問機會，培養學生提問的習慣；同時，充分聯結課內外提問機會，從多個角度將提問融入學生的日常學習與生活。

（一）依托設計，課內搭好支架

1.運用引導語，誘發學生提問。在學生提問時，教師設置提問窗口，發揮好引導語的作用，常見的引導語：學到這里，你有什么疑問嗎？你有什么問題想問嗎？你還有什么問題？等等。但是，每節課都用這些，久而久之就會流于形式，學生也會產生疲倦感。教師可以嘗試其他方式進行提問，如仔細觀察，你有什么不明白的嗎？這里你有看不明白或想不明白的地方嗎？等等。不同形式的提問語言，目的都是誘發學生提問，教學時要及時切換引導語。

2.改變呈現方式，引發學生提問。新課標要求“創造性地使用教材，積極開發、利用各種教學資源”，教學內容不同的呈現方式對學生學習起到的作用存在個體差異。這就需要教師根據學生的實際情況進行合理備課，可以將后續內容前置更換成生活化、趣味性的教學情境，也可以將問題精簡，讓學生更積極、主動地發問等。這樣既符合學生學習心理，又有助于引發學生提問。

3.借用評價語，觸發學生提問。羅森塔爾效應表明，正向的暗示與評價，會對人起到激勵的作用。在學生提問時，筆者主要采用肯定性評價與鼓勵性評價，以此激發學生的提問熱情。肯定性評價：此評價方法用于學生能正確提出問題、問題探究價值高等情況，評價語不能是簡單的一句“你真棒”，而應是全班性的鼓掌（老師覺得你提的問題很有深度，我們把掌聲送給他）、板書記錄（這個問題很有研究價值，老師把它記錄在黑板上）、名人故事（你的想法跟數學家一樣，真了不起）等等。這樣的評價語首先是不單調，能讓學生體會到成就感，其次是給其他學生做提問的示范。鼓勵性評價：此評價方法用于學生不能準確提出問題、問題探究價值低等情況，評價語不能是簡單的一句“你再想想”，而應借用“肯定—建議—鼓勵”的三明治法評價。比如，老師覺得你現在已經會提問題，真替你開心，但問題這樣改一下可能會更好，相信你之后會提出更有深度的問題。

（二）提供機會，課外創設平臺

1.創建班級“提問角”。提問角是學生在課堂上還沒有弄明白的知識點或者在練習、生活中遇到不懂的數學問題進行提問展示的平臺。學生可以將自己的困惑或問題放上去，以尋求他人的幫助。其他學生可以對這里的問題進行回答，回答完畢后交給數學老師檢查是否規范與準確，符合要求的將其交還給提問者，不符合要求的需粘貼回原位并附上姓名，等待下一個解答者，解答正確的學生可以獲得1-3個兌換幣。

2.設立提問“爭星欄”。爭星欄旨在營造學生積極參與提問、解答的數學學習氛圍。依據課堂上學生的提問次數與質量、提問角的提問質量與解答情況，來獲取相應的兌換幣，積攢到一定數量可以去數學老師處兌換相應的獎勵（前期設計好獎勵方式），如免作業1次、獎勵練習本1本等，激發學生提問興趣，真正將“以問引學”的教學理念融入學生學習。

在大力推進“學為中心”的課程改革背景下，學生發現問題與提出問題的能力培養至關重要，有助于學生數學思維的打開。作為一線教育工作者，需要明確阻礙學生提問的原因所在，進而通過確定學生的認知起點與需求、確定問題的探究設計點、確定提問形式與環節的方向，促使學生增強數學提問意識，精準落實與達成數學“四能”，有效提升學生的數學提問思維。

［參考文獻］

［1］顧志能，邱月亮.“生問課堂”教學模式的探索與實踐[J].小學數學教師，2020（Z1）：6-9.

［2］俞亞，馬紅.如何進行“引問”與“釋問”[J].小學數學教師，2020（Z1）：32-36.

［3］諸錦娟.提升學生數學提問力的幾點思考[J].小學數學教育，2020（22）：28-29.

［4］朱國榮.“求學問，需學問”：落實“增強發現和提出問題的能力”之思考[J].教學月刊小學版（數學），2018（Z1）：11-15.

朱家浩? ?浙江省嘉興市海鹽縣橫港小學。