一道橢圓三點共線問題的探究

北京市陳經綸中學 (100020) 孫丕訓 潘欣桐

在我們研究一個數學問題本質或探索某問題的內在規律時，適當地對題目條件進行弱化是一種非常有效的方法.本文從2021年朝陽區二模解析幾何解答題出發，將其條件進行適當弱化，得到該問題背后的規律，并將得到的規律推廣到雙曲線中.

1.試題呈現

2.試題求解

解：(Ⅰ)易得△FMN的面積為1，過程略.

評注：本題證明三點共線，其中A是給定點.顯然這道題也可不給出點A的坐標，改為證明直線HG過定點.那么問題的難度顯然加大了.

3.試題推廣

筆者經過探討，發現了問題的一般情形，得到如下的一般結論：

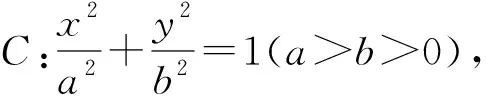
類比雙曲線，不難得到以下結論：

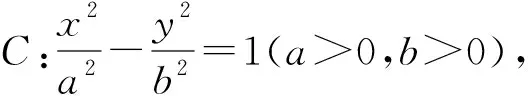
橢圓和雙曲線都是有心曲線，標準方程形式很接近，橢圓的很多性質都可類比到雙曲線中，那么拋物線是否也有這樣的性質呢？

經過研究，發現了如下的性質：

結論3 已知拋物線C:y2=2px(p>0)，過點(m,0)作直線l交C于M,N兩點，點A(a,0)，直線AM,AN分別交直線x=-m于P,Q兩點，線段MN,PQ的中點分別為G,H.則直線GH過定點,

以上三個結論中，如果聯想到橢圓(雙曲線)中的共軛直徑、極點、極線，筆者借助幾何畫板發現了更一般的結論，因為還未找到合適的證明方法，只能先作為猜想.

猜想1已知圓錐曲線C:mx2+ny2=1(mn≠0)，直線l經過定點B(x0,y0)且與曲線C交于不同的兩點M,N.E(s,t)是過點B且與直線mx0x+ny0y=1垂直的直線上的定點.設直線EM,EN分別與直線mx0x+ny0y=1交于兩點P,Q，線段MN,PQ的中點分別為G,H，則直線GH必過定點.

猜想2已知拋物線C:y2=2px(p>0)，直線l經過定點B(x0,y0)且與曲線C交于不同的兩點M,N.D(s,t)是過點B且與直線y0y=p(x+x0)垂直的直線上的定點.設直線EM,EN分別與直線y0y=p(x+x0)交于兩點P,Q，線段MN,PQ的中點分別為G,H，則直線GH必過定點.