具有差異化服務的混合對等網絡性能分析

張長振, 馬占友,*, 劉 琳, 陳 利

(1. 燕山大學理學院, 河北 秦皇島 066004; 2. 燕山大學里仁學院, 河北 秦皇島 066004)

0 引 言

對等(peer-to-peer,P2P)網絡在通信和資源共享中起著重要的作用。近年來,P2P網絡由于其可擴展性和簡單、經濟高效的模型而變得越來越重要。具有分散文件存儲的P2P文件共享系統已經出現,允許對等方共享資源并直接從彼此下載文件。然而,阻礙這些服務成功的一個主要問題是一種稱為“搭便車”的行為,在這種行為中,對等方免費享用系統資源,而從不共享任何資源。這類用戶的存在會影響服務的健康,因為它們會給其他節點和系統帶來麻煩,如延誤和資源浪費,降低P2P系統的有效性,加劇網絡擁塞,導致系統的不穩定性,影響P2P系統滿足其共享和協作的總體目的的能力[1]。Adar等[2]發現Gnutella中66%的對等點是從不分享資源的“搭便車”用戶,47%的資源來自前1%的對等點,98%的資源來自前25%的對等點。

為了應對P2P網絡中的“搭便車”行為,目前已經研究了許多方法,主要分為4類,分別是互惠策略(對等點優先提供資源給那些曾經提供過資源的對等點)、懲罰策略(對“搭便車”用戶施加懲罰來減少“搭便車”行為)、激勵策略(設計一種激勵機制來鼓勵用戶共享資源)、信譽策略(這種策略依據對等點之前的信譽來提供資源服務)。每一種策略都有許多學者做了大量的工作。

(1) 互惠策略。Alotibi等[3]為了應對P2P網絡中的“搭便車”問題,提出一個可擴展的方案,利用基于點的方法檢測“搭便車”用戶并限制他們的活動,通過提供下載優先權來獎勵共享資源的用戶。Ghaderzadeh等[4]提出了一種更智能的方法,其想法是對等點之間分享信息,對等點通過這些信息來選擇最佳的對等點來進行資源共享。Zghaibeh[5]提出O-Torrent機制來應對“搭便車”行為。在此機制下,所有對等點只有共享資源才能下載使用系統的資源。

(2) 激勵策略。Wu等[6]提出了一種基于博弈論的P2P文件共享激勵機制,稱為本地激勵機制。根據網絡中的交易數量和“搭便車”用戶百分比,以下載帶寬作為衡量標準進行評估。Singha和Singh[7]提出了一種新的激勵機制,每個對等點根據自己的貢獻獲得相應的收益,以此來激勵對等點共享資源。Awasthi和Singh[8]提出了一個基于貢獻指數的激勵策略。

(3) 懲罰策略。Yahaya[9]通過仿真研究了一種線性模型在P2P系統中緩解“搭便車”的有效性。Ojo等[10]利用博弈論提出了一種新的對等輔助流模型,提出了一個獎懲機制,對“搭便車”用戶施加懲罰來鼓勵資源共享。Manoharan和Ge[11]提出一個扣分策略來應對P2P網絡中的“搭便車”行為。

(4) 信譽策略。Alhussain和Kurdi[12]提出了一種信譽管理系統,通過將每個對等方的信譽信息保存到一個鏈來完成。Marti和Garcia-Molina[13]介紹了信譽系統組件及其屬性的分類,并討論了用戶行為和技術約束之間的沖突。Tseng和Chen[14]提出了一種P2P文件共享網絡中的“搭便車”用戶感知信譽系統,提供了一種簡單的方法來減少惡意文件的傳播和免費使用。Fan等[15]提出了一種新的信任模型,采用該技術計算信任評級特征向量和推薦矩陣,定義推薦聲譽值來評估資源服務行為。Domingo-Ferrer等[16]論證了利用信譽提供激勵來補償負收益,從而使共同效用得以實現。Sanchez等[17]建立了完全分散的P2P共享管理網絡和信譽管理協議,解決了影響資源共享的兩個主要障礙,即缺乏對匹配機構的信任和隱私問題。

本文提出的差異化服務策略相當于一個懲罰策略。當對等點發出服務請求時,超級節點根據其存儲的對等點的歷史信譽值,區分“搭便車”用戶和資源共享用戶,對兩類用戶提供差異化服務,“搭便車”行為用戶被分配給移動節點處理請求,其速率較低,而資源共享用戶被分配給固定節點處理請求,其速率較高。目的是增大“搭便車”用戶的平均等待時間,從而降低其個人平均收益,鼓勵對等點資源共享。為了驗證本文所提出的懲罰策略的有效性,本文將在數值實驗中對兩類對等點的個人平均收益進行對比分析。

對于不同類別服務臺的排隊系統和休假排隊系統的研究,Madan等[18]研究了單重異步Bernoulli休假策略下的M/M/2排隊模型,探討了兩種休假方式,得到了模型的穩態方程組。Kumar和Madheswari[19]研究的多重休假下的異步M/M/2排隊模型,利用矩陣幾何解的方法得到了隊長的穩態分布,分析了系統的忙期以及等待時間等指標。王玲等[20]研究了兩個不同服務臺的M/(Ek,M)/2可修排隊系統,通過數值算例分析了服務率,到達率對系統平均隊長的影響。金順福等[21]基于固定節點的延遲修復策略,研究了混合P2P網絡中固定節點延遲修復策略的性能分析,利用矩陣幾何解方法,進行系統模型的穩態分析。Yu等[22]利用帶有多重工作休假、啟動器、反饋和N-策略的可修M/M/2排隊模型研究了具有閾值激活過程和干擾信號的無線通信網絡,并提出降低系統能耗的策略。Ayyappan等[23]研究了單個帶有準入控制和伯努利休假的服務臺服務兩類顧客的問題。Ugochukwu和Onyebuchi[24]研究了中途退出,服務器故障,服務器休假對批量到達排隊系統的各種狀態的影響。Fan等[25]將休假排隊模型應用于區塊鏈系統,研究了區塊生成過程中的一些性能指標。Tamrakar和Banerjee[26]研究了單個服務器、無限緩沖區、具有單個和多個休假的批量服務泊松隊列,并通過進行數值實驗驗證了分析結果。Angelika和Abdelhak[27]研究了帶有等待和K-變休假的單服務器馬爾可夫伯努利反饋排隊系統。Niranjan[28]研究了帶有休假和狀態依賴故障服務臺的批量到達和批量服務排隊系統。與以上工作不同,本文對服務臺數量進行一般化,即將兩類服務臺的數量拓展到c和d個,以應對“搭便車”行為為目的,建立了M/M/c+d混合P2P網絡排隊模型。

本文將排隊論的方法應用于混合P2P網絡,根據用戶的歷史交易行為和信譽記錄,將請求節點劃分為兩類,對疑似有“搭便車”行為的請求節點提供較低服務率的服務,對資源共享的請求節點提供高服務率的服務,以減少“搭便車”用戶的個人平均收益,來應對“搭便車”問題,鼓勵用戶共享資源。建立了帶有負顧客和同步多重工作休假的M/M/c+d排隊模型,對混合P2P網絡進行建模分析,利用矩陣幾何解的方法求解排隊系統的穩態分布,構建平均移動節點數量,請求節點個人平均收益等性能指標。使用Matlab 2018a進行數值實驗,比較兩類請求節點的個人平均收益,驗證模型有效性,進行系統收益分析。

1 混合P2P網絡與建模

1.1 混合P2P網絡

本文所考慮的混合P2P網絡由不同的對等簇組成,每個對等簇相當于一個對等點,簇與簇之間通過純P2P模式相連接,如圖1所示,圖中的箭頭方向表示簇之間發出的請求。每個簇包含一個超級節點,多個固定節點和移動節點。每個固定節點或者移動節點都是一個對等點,它既可以作為請求節點通過所在的簇向其他節點發出服務請求,也可以作為服務節點接收其他節點的服務請求。

圖1 純P2P模式Fig.1 Pure P2P mode

3類節點的具體作用如下:

(1) 超級節點:處理搜索請求,通過分析請求節點的歷史數據和信譽情況,將其劃分為兩類,一類是接受完服務愿意作為服務節點向其他用戶提供服務的節點(Ⅰ類請求節點);另一類是接受完服務不愿意作為服務節點而直接離開系統,即有“搭便車”行為傾向的節點(Ⅱ類請求節點)。將有“搭便車”行為傾向的請求節點分配給移動節點服務,將信譽良好的請求節點分配給固定節點服務。超級節點必須擁有足夠的內存來存放請求節點的歷史數據以及簇內固定節點和移動節點的信息目錄,而且負責維護整個簇內的網絡結構。

(2) 固定節點:為Ⅰ類請求節點提供高服務率的服務,位于Ⅰ區,數量為c,Ⅰ區帶有一個可容納無限請求的緩沖區。固定節點主要通過固定網絡接入,優點是設備性能和網絡帶寬良好,穩定性高,有較高的服務率;缺點是需要不定時的休假來維持較高的服務率。

(3) 移動節點:為Ⅱ類請求節點提供低服務率的服務,位于Ⅱ區,數量為d,Ⅱ區無緩沖區。移動節點要通過無線網絡接入,優點是移動性和靈活性好,幾乎不需要休假;缺點是網絡穩定性較低,帶寬有限,所以服務率較低。

現實中,我們不能使得每一個簇內的超級節點都存儲所有用戶的歷史信息,因為這要求極大的內存,大大增加了系統成本。我們的策略是,由于每一個用戶都是優先向相鄰的簇發出請求,而且P2P系統中的信息資源具有較大的重復性,所以簇內的超級節點只需要以自己所在的簇為中心,存儲鄰近一個范圍內的用戶的歷史信息和信譽記錄。當用戶的請求在鄰近的簇內得不到滿足時,繼續經過鄰近的簇向另一個簇發出請求,由于另一個簇內的超級節點可能沒有存儲這個用戶的歷史信息,這要求兩個簇之間的超級節點共享用戶歷史信息和信譽情況,這樣,超級節點就不需要極大的內存,又能存儲所有P2P網絡中用戶的信息。

圖2描述了混合對等網絡中每個簇的運行機制,圖中的箭頭方向表示請求節點的流動方向。

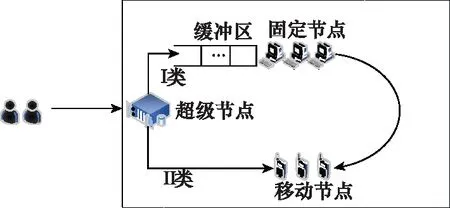
圖2 混合P2P網絡中每個簇的運行機制Fig.2 Operating mechanism of each cluster in a hybrid P2P network

1.2 模型描述

將每一個P2P網絡的簇抽象為一個具有兩類服務臺的排隊系統,把固定節點和移動節點分別抽象為兩類不同服務率的服務臺,將信譽不同的兩類請求節點分別抽象為兩類顧客。固定節點數量為c,有無限等待空間,服務時間S1服從參數為μ1的指數分布;移動節點數量為d,無等待空間,服務時間S2服從參數為μ2的指數分布(μ1>μ2>0)。Ⅰ類請求節點和Ⅱ類請求節點的到達間隔T1,T2分別服從參數λ1,λ2的指數分布(λ1,λ2>0)。

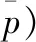
(2) 當Ⅰ區固定節點空閑時,固定節點立即進入長度為V的工作休假,休假長度V服從參數為θ的指數分布。當工作休假結束時,若Ⅰ區仍無節點請求服務,則固定節點繼續下一個工作休假時間;當工作休期結束時,若Ⅰ區有節點請求服務,則固定節點結束工作休假期,開始正規忙期;若工作休假尚未結束,Ⅰ區已有節點請求服務,則固定節點以較低的速率μ2為Ⅰ類節點提供服務。

(3) 在工作休假期,若Ⅰ區沒有空閑的固定節點,但Ⅱ區有空閑的移動節點,則新到的Ⅰ類請求節點直接進入Ⅱ區接受服務;若Ⅰ區有空閑固定節點,則新到的Ⅰ類請求節點在Ⅰ區接受服務。

(4) 系統引入負顧客,相當于干擾節點,可以將一次請求任務結束。當負顧客到達系統時,將一對一地抵消處于正常服務期的Ⅰ區任意一個請求節點,若Ⅰ區無處于正常服務期的請求節點,到達的負顧客自動消失。負顧客只起抵消作用,不接受服務,負顧客到達服從參數ε的指數分布。

假設排隊系統的服務規則是先到先服務,到達間隔、服務時間、休假時間等均相互獨立。本文主要利用帶有負顧客和同步多重工作休假策略的M/M/c+d排隊模型分析研究對等網絡中的“搭便車”問題。

2 模型分析與性能指標

2.1 模型分析

假設L1(t)表示t時z刻系統中Ⅰ區的請求節點數,L2(t)表示t時刻系統中Ⅱ區的請求節點數,J(t)表示t時刻Ⅰ區固定節點所處的狀態。

(1)

根據模型的描述可知,三維馬爾可夫過程{(L1(t),L2(t),J(t)),t≥0}是一個擬生滅過程(quasi-birth-and-death process, QBD),有狀態空間Ω={(0,j,0)|0≤j≤d}∪{(i,j,k)|i≥1,0≤j≤d,k=0,1}。

將狀態按字典序進行排列,系統的狀態轉移率矩陣有如下分塊形式:

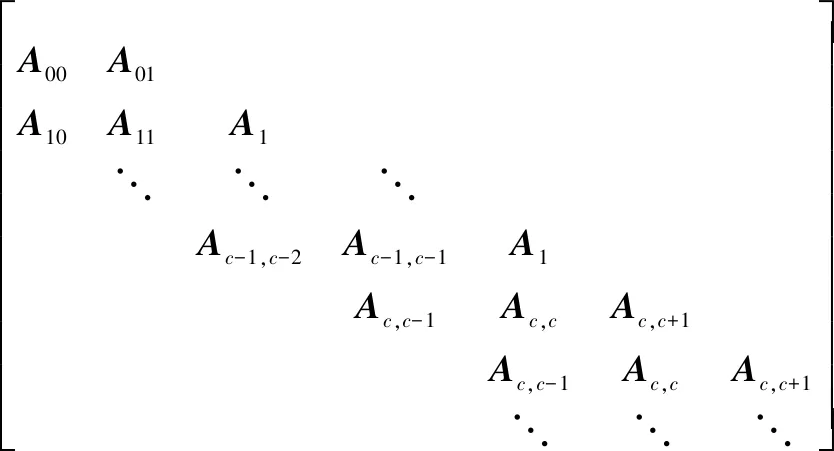
(2)

其中,A00,A01,A10,Aii(1≤i≤c-1),A1,Ai,i-1(2≤i≤c),Acc,Ac,c+1分別代表水平間的狀態轉移率,為了簡便表示矩陣,定義如下符號:

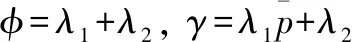
Q矩陣的各個子塊矩陣具體如下:

(3)

(4)

(5)

當1≤i≤c-1時,

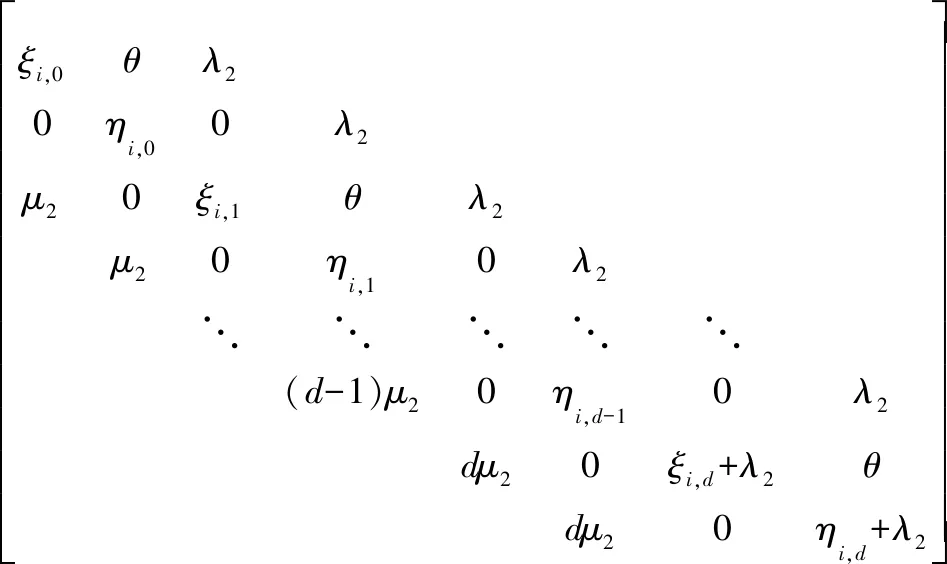
(6)

(7)

當2≤i≤c時,

(8)

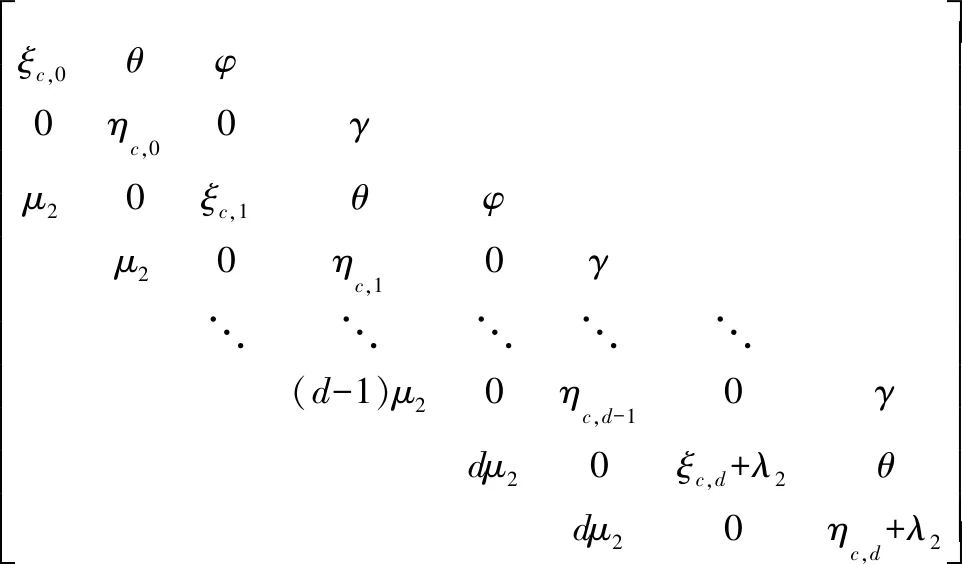
(9)

(10)

其中,A0,0是d+1維的方陣,A1,0是(2d+2)×(d+1)維的矩陣,A0,1是(d+1)×(2d+2)維的矩陣,其余的子塊矩陣均是2d+2維的方陣。

當馬爾可夫過程{(L1(t),L2(t),J(t)),t≥0}正常返時,穩態分布有如下形式:

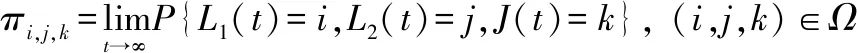
QBD{(L1(t),L2(t),J(t)),t≥0} 正常返的充分必要條件是矩陣方程:

R2Ac,c-1+RAc,c+Ac,c+1=0

(11)

有最小非負解R,且譜半徑SP(R)<1,隨機陣

(12)

有左零向量。當QBD正常返時,穩態分布為

(13)

其中,e1和e2分別是d+1維和2d+2維且所有元素均為1的列向量。

上述結論的證明過程運用了矩陣幾何解方法,具體證明過程可參見文獻[29-31]。

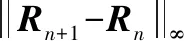
算法 1 迭代算法步驟 1 對系統參數定義初始值η(η=10-10),c,d,ε,θ,λ1,λ2,μ1,μ2,設置率陣R=0步驟 2 輸入 Ac,c-1,Ac,c,Ac,c+1步驟 3 定義 Rn=RR=-(R2Ac,c-1+Ac,c+1)A-1c,cRn+1=R步驟 4 如果 Rn+1-Rn∞>η 返回步驟3否則 進入步驟5步驟 5 R=Rn+1

2.2 性能指標

(1) Ⅰ區請求節點平均隊長為

(14)

(2) Ⅱ區請求節點平均隊長為

(15)

利用排隊理論中的Little公式[32-33]可得

(3) Ⅰ區和Ⅱ區請求節點平均逗留時間為

(16)

(4) Ⅱ類請求節點到達后消失的概率為

(17)

(5) Ⅰ區無空閑,Ⅰ類請求節點到達后等待的概率為

(18)

3 數值實驗

通過迭代算法得到R2Ac,c-1+RAc,c+Ac,c+1=0的最小非負解R,然后利用穩態分布方程組求解,可以得到πi,j,k的數值結果,進而可以得到混合P2P系統的各項性能指標。在實際生活中,性能指標會隨參數的變化而變化。利用Matlab 2018a給出數值例子來刻畫性能指標隨系統參數的變化趨勢。

3.1 系統性能分析

圖3反映了當μ1=5,μ2=1,c=6,θ=1,p=0.6,ε=1時,Ⅰ區請求節點的平均等待時間E(W1)隨工作休假參數θ和固定節點數量d變化的趨勢。當d固定時,隨著θ的逐漸增大,E(W1)逐漸減小;當θ固定時,隨著d的逐漸增大,E(W1)逐漸減小。這是因為θ越大,Ⅰ區服務臺工作休假的時間越短,正常工作時間越長,因此請求節點等待的時間越短;d越大,可供Ⅰ類請求節點選擇的服務臺數量越大,等待時間就越短。

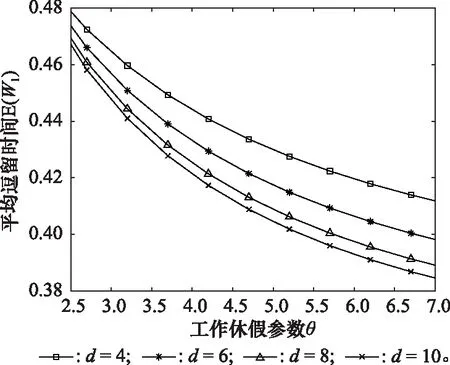
圖3 E(W1)與d和θ的關系Fig.3 Relationship of E(W1) with d and θ

圖4反映了當μ1=5,μ2=1,c=6,d=6,θ=1,p=0.6,ε=1時,Ⅱ區請求節點的平均隊長隨兩類請求節點到達率變化的趨勢。當Ⅰ類請求節點和Ⅱ類請求節點的到達率增大時,Ⅱ區請求節點的平均隊長逐漸增大。這是因為當Ⅰ區無空閑固定節點時,Ⅰ類請求節點會以概率1-p進入Ⅱ區接受服務,所以Ⅰ類請求節點和Ⅱ類請求節點的到達率增大都會使得Ⅱ區請求節點的平均隊長增大。

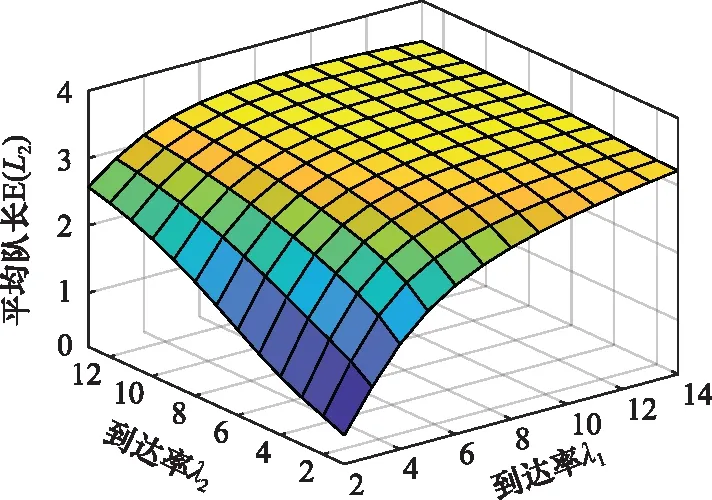
圖4 E(L2)與λ1和λ2的關系Fig.4 Relation ship of E(L2) with λ1 and λ2

當c=6,d=5,λ1=6,λ2=3,μ1=10,μ2=5,θ=4,p=0.6時,觀察負顧客的到達率變化對系統性能指標的影響。從表1可以看出隨著ε的不斷增大,E(W1),E(L1),E(W2),E(L2)分別不斷減小,但Pd沒有明顯的變化。這是因為負顧客的到達會抵消一個Ⅰ類請求節點,而Ⅰ類請求節點會以一定概率進入Ⅱ區接受服務,所以E(W1)等4個指標都會隨負顧客到達率的增大而減小。而負顧客只抵消正常工作狀態的固定節點,不抵消移動節點,所以Pd隨ε改變,沒有明顯變化。

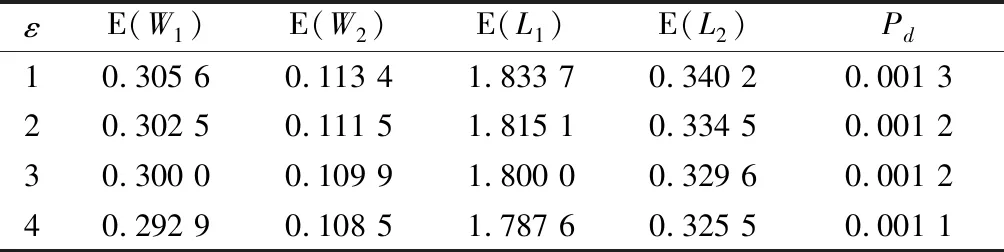
表1 ε對系統性能指標的影響

3.2 模型有效性驗證

本文為應對P2P網絡中的“搭便車”行為,提出一個懲罰策略,對“搭便車”行為用戶和資源共享用戶提供不同服務率的服務,本節對此懲罰策略進行有效性驗證。

假設一個請求節點完成一次服務請求之后獲得的個人回報為M,請求節點在系統內單位平均逗留時間的時間成本為F,則請求節點完成一次服務請求所獲得的個人平均收益有如下表達式:

U1=M-F·E(W1)

(19)

U2=M-F·E(W2)

(20)

其中,U1表示Ⅰ類請求節點的個人平均收益函數,U2表示Ⅱ類請求節點個人平均收益函數。當c=d=7,λ1=λ2=2,ε=3,p=1,μ1=2,μ2=0.5,M=20,F=15,即,兩類請求節點的到達率相等,但固定節點和移動節點的服務率不同時,觀察隨工作休假參數θ變化,兩類請求節點的個人平均收益U1,U2的大小。由圖5可以看到,隨著工作休假參數的增大,兩類請求節點的個人平均收益均逐漸增大。這是因為如果工作休假參數增大,平均休假時間減小,服務節點處于工作狀態的概率增大,因此請求節點的平均逗留時間減小,通過收益函數的表達式可知,請求節點的個人平均收益與平均逗留時間負相關。因此,兩類請求節點的個人平均收益增大。

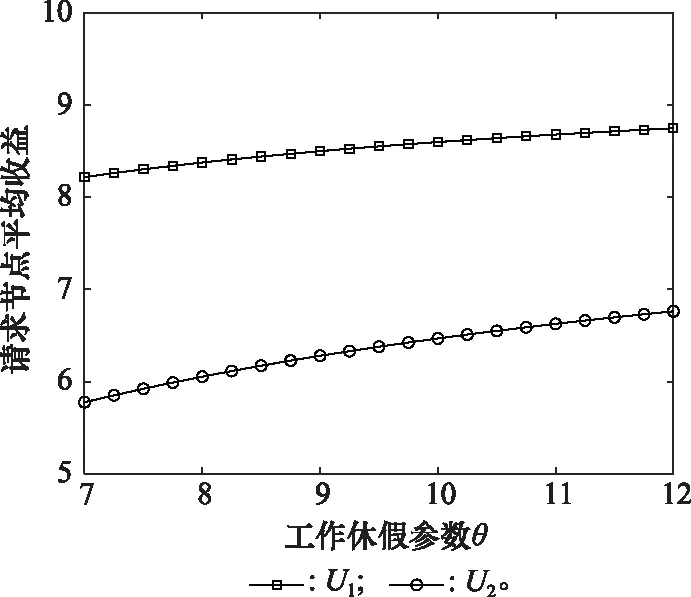
圖5 U1,U2與θ的關系Fig.5 Relationship of U1,U2 with θ

另外,Ⅰ類請求節點的平均收益函數曲線始終在Ⅱ類請求節點的平均收益函數的上方,即,無論哪個參數水平,Ⅰ類請求節點的平均收益始終大于Ⅱ類請求節點的平均收益。為了看到準確的收益對比,表2給出了兩類請求節點個人平均收益的數值比較。表2顯示,無論在哪一個工作休假參數水平下,Ⅰ類請求節點的個人平均收益相比于Ⅱ類請求節點的個人平均收益,至少高出20%。因此,本文所建立的應對“搭便車”行為的模型可以有效降低“搭便車”用戶的平均收益,懲罰作用明顯。

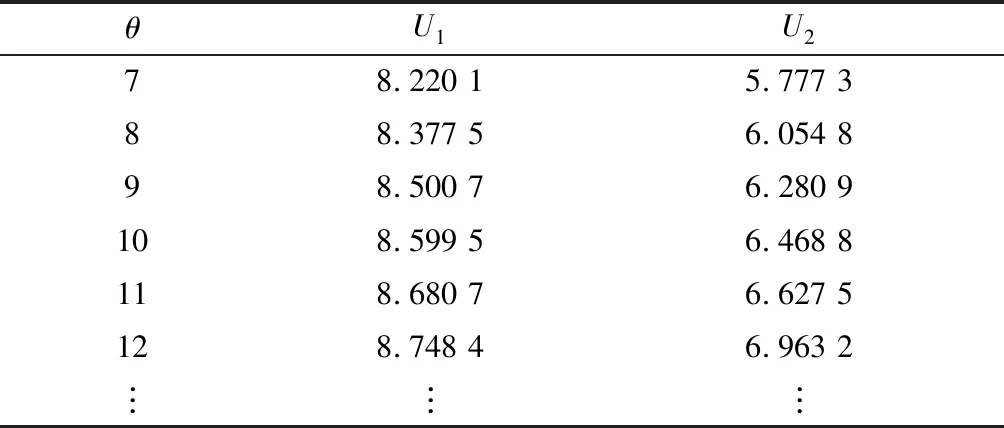
表2 U1,U2的具體值

4 系統收益分析

本節討論P2P系統的收益問題。假設L表示P2P系統服務完一個節點后獲得的平均收益,C表示單位時間內P2P系統服務一個節點的平均成本,Cp表示每個節點在正規忙期內的損失,Cd表示一個Ⅱ類請求節點消失后帶來的潛在損失,則P2P系統的收益函數可以表示為

(21)

其中,

為了保證該P2P系統盈利,需要滿足

即

圖6反映了當λ2=2,μ1=10,μ2=5,c=6,d=5,p=0.6,ε=3,L=22,C=5,Cp=14.1,Cd=5時,系統收益隨λ1和θ變化的趨勢。當θ固定時,隨λ1逐漸增大,收益U逐漸減小,最終小于零;當λ1固定時,收益U隨θ的增大而變大。這是因為λ1增大,但若服務臺服務率相對較小,有一部分請求節點到達后離開,造成的潛在損失加大;而當θ增大時,系統的休假時間減小,正常工作時間增大,給系統帶來的收益增大。所以,為了提高系統收益,一方面需要使服務率相對于到達率較大,從而降低請求節點離開的概率,另一方面需要降低系統的休假時間。

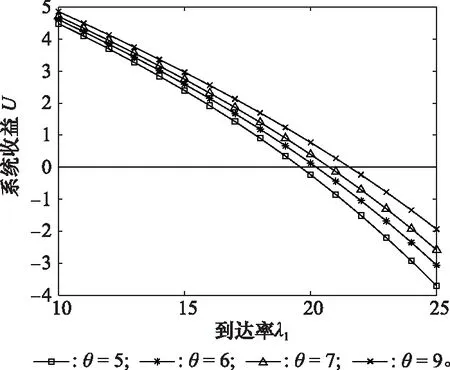
圖6 U與λ1和θ的關系Fig.6 Relationship of U with λ1 and θ

為了保證系統收益大于零,需找到使得系統收益大于零的點。由Matlab 2018a可以得到,當λ1<19,θ=5;λ1<20,θ=6;λ1<20,θ=7;λ1<21,θ=9時,P2P系統收益大于零。

5 結 論

P2P網絡中的“搭便車”行為嚴重影響了系統的效率和穩定性。本文提出一個懲罰策略來應對“搭便車”行為,即根據對等點的歷史信譽值,將其分為兩類,對其提供差異化服務,減少“搭便車”用戶的個人收益。利用M/M/c+d排隊模型,對此混合P2P網絡進行排隊建模,使用矩陣幾何解方法求解排隊模型的穩態分布,通過數值實驗驗證了模型的有效性。實驗結果顯示,無論在哪一個工作休假參數水平下,Ⅰ類請求節點的個人平均收益相比于Ⅱ類請求節點的個人平均收益,至少高出20%。最后通過構造系統收益函數,研究了混合P2P系統的收益,得到保證混合P2P系統收益的參數閾值。本文將排隊建模方法應用于P2P網絡,分析P2P網絡中的實際問題,為以后的研究提供了思路。

對于P2P中的“搭便車”現象,需要提出更加合理有效的“搭便車”行為劃分方法,結合排隊理論,構造更加有創新性的P2P網絡系統。針對此問題，我們將在以后的工作中繼續研究。