主余震序列作用下邊坡位移響應及地震動參數相關性分析

殷京科，李典慶，杜文琪

(武漢大學水資源與水電工程科學國家重點實驗室，工程風險與防災研究所，湖北，武漢 430072)

近年來，我國地震頻發，造成了嚴重的經濟損失和人員傷亡。作為我國地震多發地區，西部各省多山地地形，邊坡眾多。強震作用下，極易造成邊坡失穩，從而引發滑坡等次生災害。據統計，2008年汶川8.0級大地震觸發5萬余處滑坡，規模較大的包括位于綿竹市安縣的大光包巨型滑坡(方量達7.4×108m3)、位于北川縣城的城西滑坡(方量達4.8×106m3)，其中城西滑坡導致1600人遇難[1-3]。2010年玉樹7.1級地震共觸發兩千多處中小型滑坡[4]，2013年蘆山7.0級地震誘發3800余處滑坡[5]。2013年岷縣6.6級地震造成3處大型黃土滑坡，致12人遇難并毀壞房屋100余間[6]。上述災害后果表明，合理評估邊坡在強震作用下的動力響應與滑動位移，對預測地震動的潛在破壞勢以及開展快速地震風險評估十分重要。

目前，邊坡的地震響應已經得到了國內外研究人員的廣泛關注。LENTI和MARTINO[7]通過數值分析，研究了地震波與邊坡之間的相互作用對滑坡位移的影響。DU[8]通過數值分析研究了自然邊坡在三維地震動輸入條件下的滑動位移特征。LI等[9]通過數值模擬研究了土體參數空間變異性對地震邊坡滑移風險的影響規律。王斌等[10]通過振動臺試驗研究了地震作用下的巖質高陡邊坡的加速度響應規律及破壞形式。李典慶等[11]基于子集模擬提出了一種用于邊坡風險分析的高效隨機有限元方法。張澤林等[12]針對西北地區的黃土泥巖邊坡的動力響應和破壞特點展開研究。WANG等[13]分析了黃土層厚度及坡度對邊坡放大效應的影響。ZHAO等[14]通過振動臺試驗對隨機地震作用下的邊坡動力響應展開研究。WANG 等[15]通過有限差分法對地震動幅值和持時對分層邊坡動力響應的影響開展了深入研究。通過上述邊坡地震響應分析的相關研究，研究人員對地震作用下的邊坡響應大小以及相應的損傷演化特征有了較為全面地認識。

一次地震的發生往往伴隨有多次余震的發生。2008年汶川大地震發生后兩個月內，觸發了20 000多次余震，其中包括數十次震級大于五級的強余震[16]。2013年蘆山地震過后的三天內，發生余震高達3000余次，震級大于五級的余震大約有四次[17]。余震是由能量未釋放完全的主震斷層或者臨近斷層的破裂產生，因此余震與主震在發震時間和空間位置分布上存在一定的相關性，而主余震的時空分布特性對工程結構的動力響應也有較大影響。因此，有必要對主余震聯合作用下的邊坡響應進行有效評估。事實上，目前針對建筑結構在主余震作用下的損傷已經得到了研究人員的關注，且較多關注“主震+最大震級余震”作用下的動力響應。例如：朱瑞廣等[18]通過振動臺試驗研究了真實主余震序列作用下的非延性框架的動力響應，并指出主余震序列的頻率特性與結構損傷存在較為密切的聯系。于曉輝等[19- 20]通過對主余震序列作用下的結構損傷進行計算，發現部分余震會使結構產生顯著增量損傷，并且對比了采用不同主余震構造方法得到的人工主余震序列作用下的結構損傷。ZHOU 等[21]對地震動強度參數與主余震作用下的結構損傷的相關性進行了分析，并建立了基于最優參數的主余震損傷預測模型。周洲等[22]通過研究主余震作用下的結構增量損傷比來定量評估余震對結構損傷的影響。韓建平和李軍[23]對主余震作用下的低延性結構進行了易損性分析。申家旭等[24]基于Copula 理論建立了能夠較好表示序列地震空間相關性的序列型地震動隨機模型。然而，目前國內外對邊坡在主余震序列作用下的響應特征研究還較少。其中，陳金昌[25]對邊坡在人工主余震序列作用下的加速度響應和橫向位移做了初步分析。然而，該研究采用了重復法構造人工主余震序列，無法真正反映真實主余震序列的特征，也無法真正考慮主震和余震強度之間的相關性，致使分析結果無法真實反映余震對邊坡動力響應的影響。由于對邊坡在主余震序列作用下的響應研究不足，使得研究人員無法真正掌握邊坡在發生主震損傷后進一步遭受余震作用時的安全性。

為解決目前對邊坡的主余震響應研究較少的問題，本文從太平洋地震工程研究中心的NGAWest2強震數據庫篩選了210條真實主余震序列，基于有限差分軟件FLAC對主震單獨作用下和主余震序列作用下的邊坡位移響應進行數值模擬，針對余震對坡肩的豎向永久位移的影響進行定量分析。基于已獲得的邊坡主余震的位移響應，對邊坡豎向永久位移與15個地震動參數的相關性展開研究，選取最優參數并建立考慮余震效應的邊坡主余震位移的預測模型。

1 主余震序列的挑選與構造

鑒于主余震的發生機理與時空分布特性非常復雜，本文未考慮主-余震的空間相關性對邊坡動力響應的影響，而是直接挑選真實主余震序列作為地震輸入來分析邊坡響應。通常一次強主震之后會發生多次余震，本文在構造真實主余震序列時僅考慮具有最大震級的余震，即一條主余震序列包含一次主震和一次最大余震。本文基于太平洋地震工程研究中心的NGA-West2強震數據庫進行主余震序列地震動挑選，主要依據如下：1)為了獲得較明顯邊坡位移響應，選擇矩震級Mw大于6.5的主震；2)主震和余震的記錄臺站位于自由場地或者較低矮的結構；3)用于構造真實主-余震序列的主震地震動和最大震級余震地震動須由同一臺站記錄，避免臺站的位置差異對主余震地震動相關特性的影響；4)場地的平均剪切波速VS30不小于100m/s。根據上述挑選原則，挑選獲得了210組主震和余震記錄，它們分別來自8個地震事件。各個地震事件的基本信息(震級及發生時間等)如表1所示。圖1給出了所挑選主余震記錄的震級與斷層距分布情況。由圖可見：斷層距離在0 km～250 km，主震和余震的震級差大約為1級，基本滿足Bath 定律[26]。

圖1 挑選的主、余震記錄的震級和斷層距分布Fig.1 Distribution of magnitude and rupture distance of the selected mainshock and aftershock records

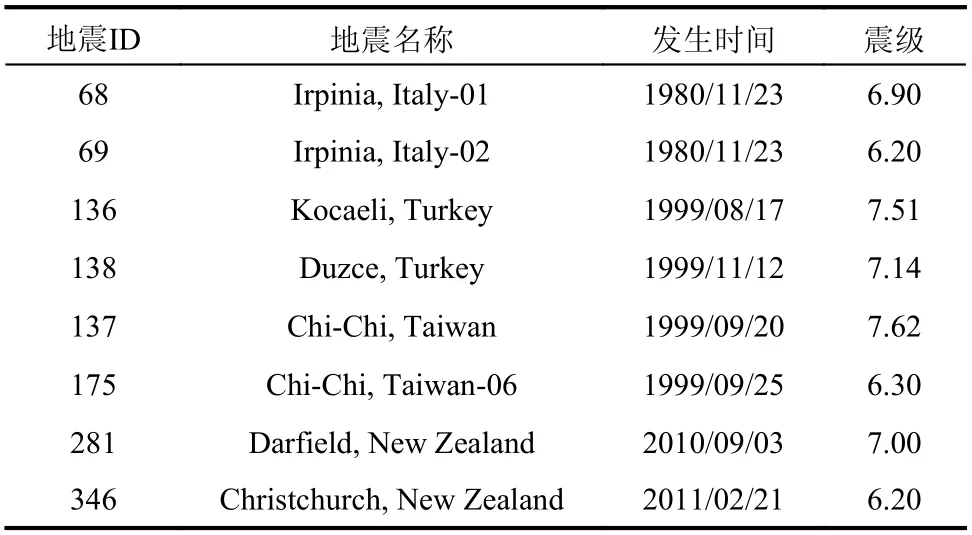
表1 挑選主、余震地震動的地震事件基本信息Table 1 Detailed information of selected mainshock and aftershock events

基于所挑選的主余震記錄計算它們的反應譜，并分別給出具有97.5%、50%和2.5%分位值的反應譜曲線，如圖2所示。對比主、余震記錄的反應譜可以發現：在圖示任意自振周期處，主震的反應譜中位值大于余震的反應譜中位值，證明了主震強度普遍高于余震強度。基于所挑選的主余震地震動，采用主震+100 s間隔+余震的形式來構成主余震序列[19]。圖3給出了一條典型主余震序列加速度時程。該序列中主震和余震在NGAWest2數據庫中的序列號分別為292和303，選自于Irpinia 地震事件。采用上述方法所構成的210條序列型地震動將用于主余震序列作用下的邊坡位移響應分析。

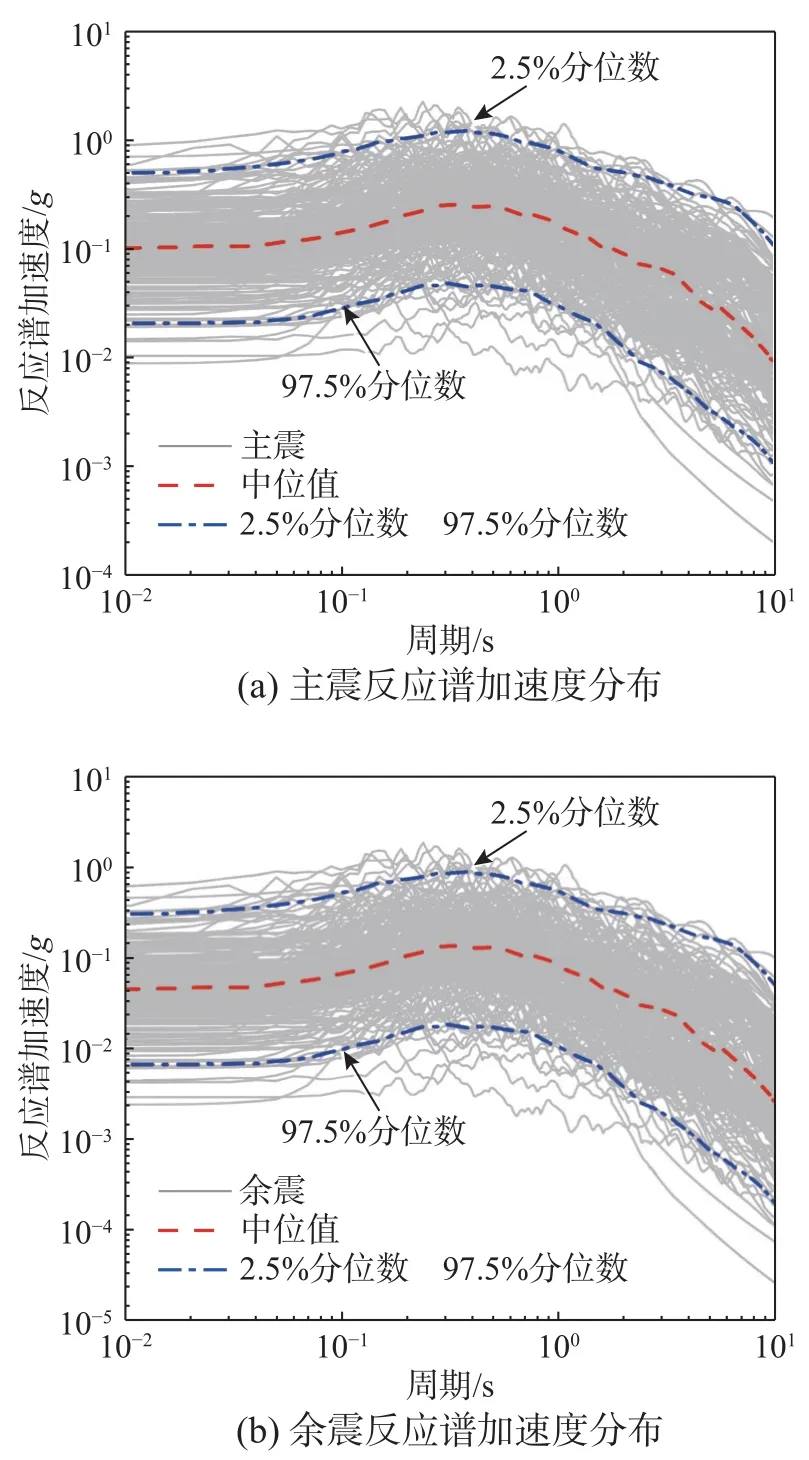
圖2 主震和余震反應譜加速度曲線Fig.2 Response spectra of mainshock and aftershock ground motions

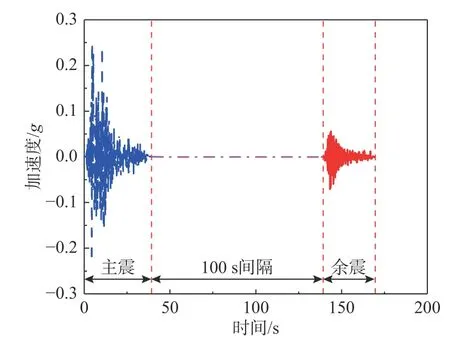
圖3 典型主余震序列加速度時程Fig.3 A typicalmain-aftershock acceleration sequence

2 多層邊坡動力響應分析模型

本文基于有限差分軟件FLAC，采用WANG 等[15]提出的多層邊坡建模方法來分析邊坡在主余震序列作用下的響應。自然邊坡中土體呈層狀分布，不同深度土體的密度和模量參數不同。與均質邊坡模型相比，分層邊坡更能反應土體的成層特性，從而得到更準確的動力響應。圖4為WANG等[15]建立的典型多層邊坡模型。模型尺寸為：長150 m×高30m。各層巖土體的材料參數如表2所示。

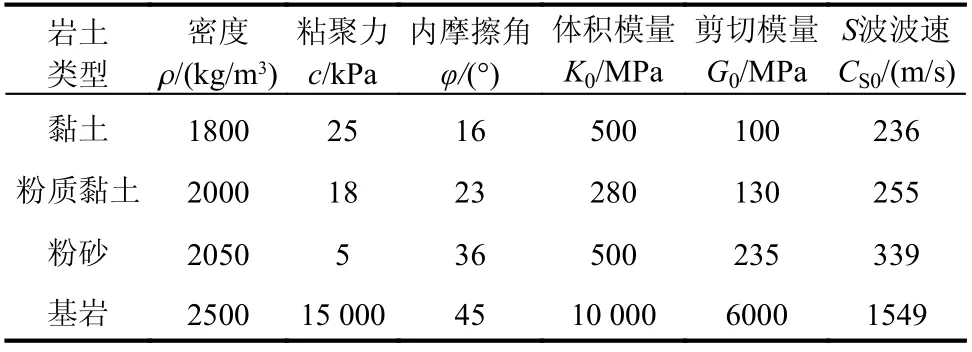
表2 邊坡模型中各土層材料參數Table2 Material parameters of each layer in the slope model

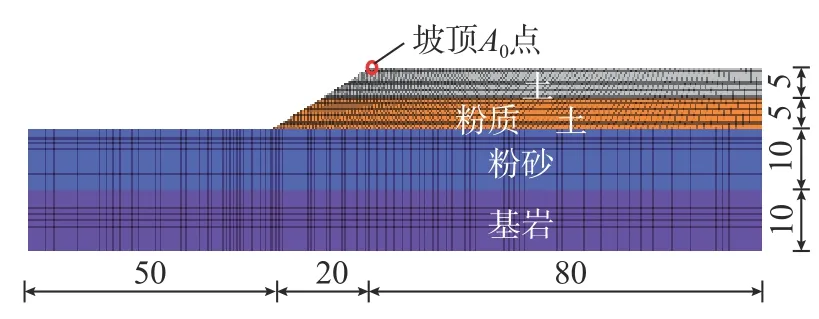
圖4 多層邊坡模型的幾何尺寸與網格劃分/m Fig.4 Geometric property and grid size of the slope model

采用摩爾-庫倫塑性本構模型來模擬土的非線性特征。模型的網格尺寸與計算結果的準確性以及計算時間的長短緊密相關。本文在確定模型的網格尺寸時，考慮以下兩方面要求：1)地震波傳播的數值精度會受到輸入地震波的頻率成分和土體剪切波速的影響，為了更為準確的模擬地震波的傳播過程，網格尺寸ΔL須小于輸入地震波最高頻率對應波長的1/8～1/10[27]；2)在動力分析中還應考慮由于模量衰減引起的橫波速度的變化，特別是對于潛在滑動區域內的網格單元。根據經驗剪切模量衰減曲線，取剪切模量衰減系數為1/16(1%～10%的應變范圍內)[28]。綜上，確定本文邊坡模型的網格尺寸ΔL為0.5 m～1.8m，其中潛在滑動區域的網格尺寸約為0.5 m。

巖土體內部的摩擦會導致部分能量的耗散，通常用力學阻尼來描述量化這一特性。本文通過設置阻尼比為0.2%的瑞利阻尼剛度分量來過濾高頻噪聲，同時設置由Hardin-Drnevich 模型[29]擬合的滯后阻尼(參考應變取0.234)，模擬巖土體在循環加-卸載過程中的模量衰減和能量耗散。在設置瑞利阻尼時，用模型自振頻率代替中心頻率，通過邊坡模型的自振分析，得到邊坡模型自振周期為0.25 s，自振頻率為4Hz。

采用多層邊坡模型分析邊坡的地震響應分析主要分為兩個階段：1)重力施加階段，將兩側邊界沿法向約束，將底部邊界沿X、Y方向約束，對邊坡單獨施加重力，提取整個邊坡模型的初始應力分布；2)動力響應分析階段，將兩側邊界設置為自由場邊界，減少邊界上波的反射，并將底部邊界X向的約束解除。在底部邊界的節點上沿X方向施加地震波速度時程，計算邊坡的動力響應，獲得坡頂A0處(坡肩)的豎向位移響應。

3 邊坡的主余震位移響應

邊坡的豎向永久位移是評估其穩定性的重要參數，其可以較好地描述邊坡在地震作用下的損傷狀態。為了評估余震對邊坡位移響應的影響，分別對邊坡在主震單獨作用下和主余震序列作用下的豎向永久位移響應進行分析和對比。為此，本文提出一個無量綱參數“位移增量比δD”來定量評估余震對邊坡位移的影響：

式中：DM和DMA分別為主震和主余震序列作用下的邊坡豎向永久位移；ΔDA表示由余震造成的邊坡豎向永久位移增量。

選擇圖4所示這一典型邊坡作為研究對象，該邊坡坡高為10m，邊坡水平長度為20m，坡比為1∶2，邊坡從上到下由黏土層(厚度5m)和粉質黏土層(厚度5m)構成；邊坡底部地基從上到下由粉砂層(厚度10 m)和基巖層(厚度10m)構成。淺層土體密度和模量較小，且土體密度和模量隨深度增加而增大。上述邊坡條件基本符合自然邊坡中的土層分布情況。為了降低左側和右側邊界對地震波傳播的影響，坡頂到右側邊界的距離設置為80 m，坡腳到左側邊界的距離設置為50m。采用第2節中的多層邊坡動力分析模型，分析獲得該邊坡在第1節中所挑選的210條主余震序列輸入下的豎向永久位移。圖5給出了在一條主余震序列作用下豎向永久位移變化曲線，可以發現主震損傷邊坡在遭受繼發余震作用后，產生了明顯的豎向位移。

圖5 主余震序列作用下坡肩豎向位移累積曲線Fig.5 Accumulation of verticaldisplacement at slope crest induced by a main-aftershock sequence

圖6給出了計算獲得的DM和DMA分布情況。由圖可見，主余震序列作用下的邊坡豎向永久位移DMA最大值約為1m，最小值約為10-6m。主震損傷邊坡在余震作用下，最大位移增量ΔDA=0.47 m。對于68.6%的主余震序列，DMA大于DM。由此可見：主震損傷邊坡在遭受余震之后會產生一定的增量位移。進一步對這部分主余震序列造成的豎向永久位移增量ΔDA和位移增量比δD進行統計分析，ΔDA和δD分布情況如圖7和圖8所示。29.6%的余震作用下產生的位移增量滿足ΔDA≥0.001 m，可認為余震能夠造成邊坡豎向永久位移一定程度的增大。此外，在所挑選的真實主余震序列中，40.0%的主余震序列作用下的邊坡位移增量比δD大于10%且小于100%，可認為余震對邊坡位移的影響顯著。另外，有6.2%的主余震序列所造成的邊坡位移增量比δD大于100%。

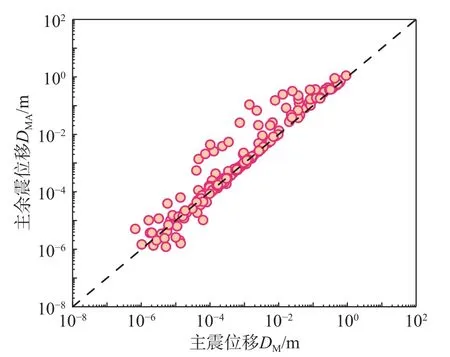
圖6 邊坡豎向永久位移D M 和D MA 分布Fig.6 Vertical permanent displacements D M and D MA of slope

圖7 位移增量分布柱狀圖Fig.7 Distribution of the incremental displacements

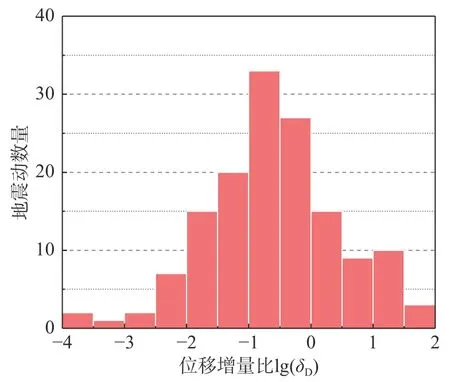
圖8 增量位移比分布柱狀圖Fig.8 Distribution of the incremental displacement ratios

4 邊坡的主余震位移響應與地震動強度參數相關性

4.1 地震動強度參數

在第3節研究的基礎上，進一步研究地震動強度參數IM與邊坡豎向永久位移D的相關性。本文挑選了15個地震動強度參數作為備選參數。其中，包括：六個加速度相關的IM(PGA、Sa(Ts)、Sa(1.5Ts)、IA、ARMS、ASI)、三個速度相關的IM(PGV、VRMS、VSI)、兩個位移相關的IM(PGD、DRMS)以及其他四個IM(Ds5～75、Ds5～95、Tm、Tp)。上述所挑選的地震動強度參數的信息，如表3所示。分別采用下標M 和A 表示主震和余震。值得說明的是，本文主要研究的是主余震序列強度與邊坡位移響應的相關性。分別采用主震強度、余震強度和余震和主震強度比作為主余震序列的強度參數指標。舉例而言，對于峰值加速度PGA來說，分別采用PGAM、PGAA和δPGA表示主震PGA、余震PGA、余震和主震PGA強度比。

表3 挑選的地震動強度參數Table 3 Selected ground motion intensity measures

4.2 相關性分析

在地震危險性分析中通常假設地震動強度參數(例如：PGA、Sa等)近似服從對數正態分布[30]。為了研究地震動強度參數與邊坡位移的相關性，本文在對數空間上分別計算了下述五種相關系數：1)主震強度與邊坡主震位移(相關系數ρ1)；2)余震強度與邊坡余震增量位移(ρ2)；3)主震強度與邊坡主余震位移(ρ3)；4)余震強度與邊坡主余震位移(ρ4)；5)余震主震強度比與邊坡位移增量比(ρ5)。

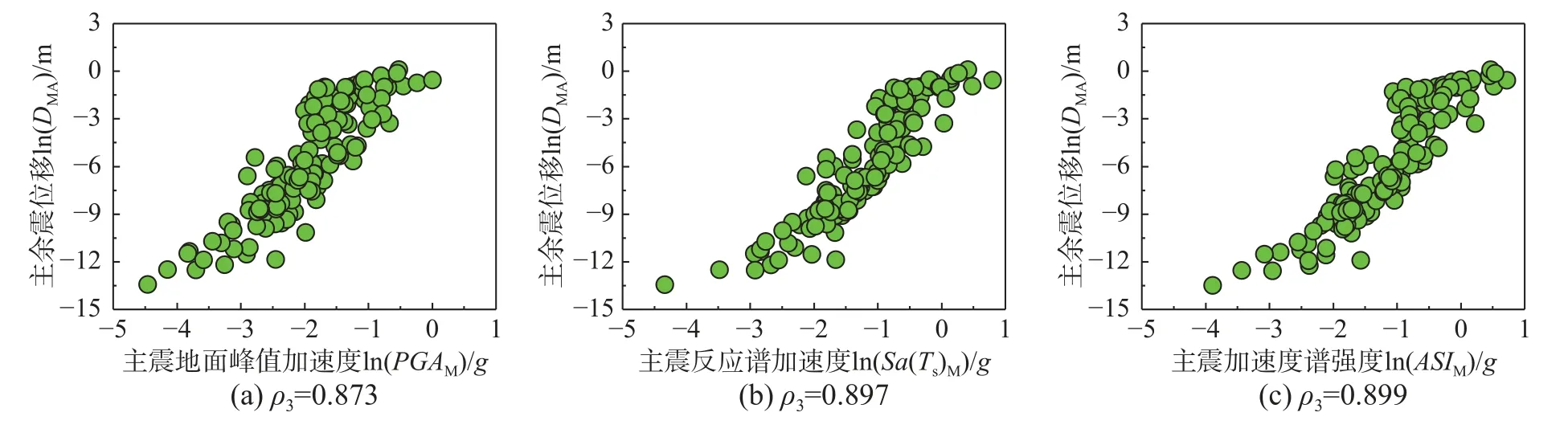
圖9給出了15種地震動強度參數所對應的上述五種相關系數值。由圖可見，加速度相關的IM(PGA、Sa(Ts)、Sa(1.5Ts)、IA、ARMS、ASI)、速度相關的IM(PGV、VRMS、VSI)以及位移相關的IM(PGD、DRMS)與位移參數呈正相關，且加速度相關的IM與位移參數的相關性相對較強；另外四個IM(Ds5～75、Ds5～95、Tm、Tp)與位移參數呈負相關。這是因為地震動強度越大，引起的邊坡永久位移越大，且地震能量集中在較短時間釋放，會造成更大的永久位移。與主震位移DM相關性最強的三個主震強度參數分別為Sa(Ts)M、ASIM和PGAM；與余震增量位移ΔDA相關性最強的三個余震強度參數分別為ASIA、Sa(Ts)A和PGAA；以上六組參數與位移的分布如圖10所示。由圖10可以看出：主震強度參數與主震位移、余震強度參數與余震增量位移都有較強的相關性，但是后者稍弱于前者。其原因是：主震損傷狀態對余震增量位移產生了影響，一定程度上削減了余震強度參數與余震增量位移的相關性。與主余震位移DMA相關性最強的三個主震強度參數分別為ASIM、Sa(Ts)M和PGAM，與主余震位移DMA相關性最強的三個余震強度參數為ASIA、Sa(Ts)A和PGAA，與位移增量比δYDis相關性最強的三個余震主震強度參數比為δASI、δSa(Ts)和δPGA，以上九組參數的分布如圖11所示。由圖11可以看出：在ρ3、ρ4、ρ5這三種相關系數中，位移增量比與余震主震強度參數比的相關系數最小，主余震位移與主震強度參數的相關系數最大，主余震位移與余震強度參數的相關系數介于兩者之間。其中，主震反應譜加速度Sa(Ts)M和主震加速度譜強度ASIM與主余震位移的相關性最強。

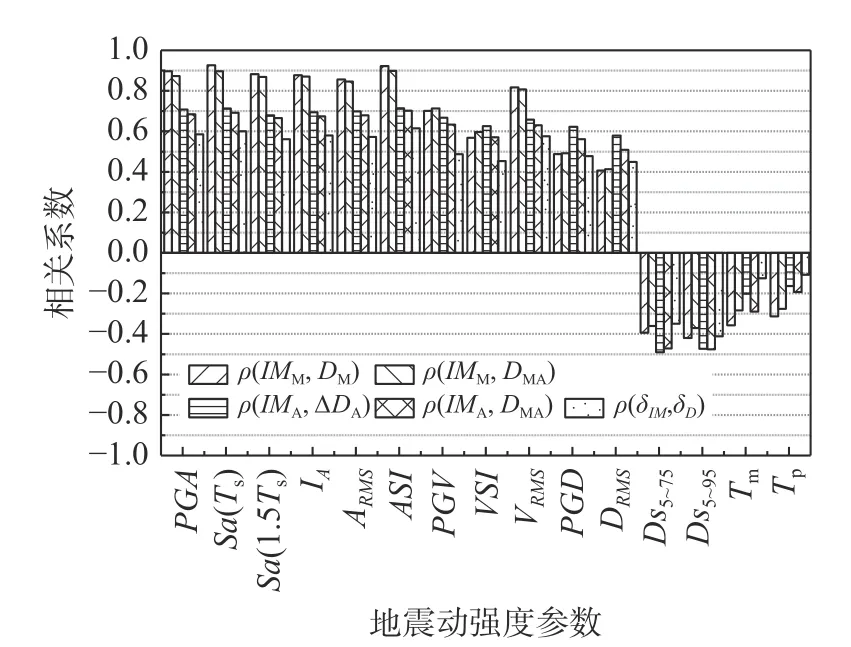
圖9 不同地震動強度參數與邊坡豎向位移的相關系數Fig.9 Correlation coefficients between different ground motion intensity measuresand the settlement of slopes

圖10 主震和余震強度參數與邊坡豎向位移(D M 和ΔD A)的相關性分布Fig.10 Correlationsbetween intensity measures of mainshocks and aftershocksand the permanent settlements(D M and ΔD A)of slopes

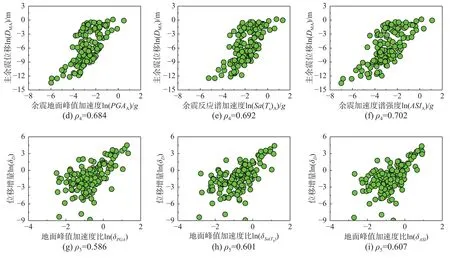
圖11 主余震強度參數與邊坡豎向位移(D MA 和δD)的相關性分布Fig.11 Correlations between intensity measuresof main-aftershocksand the permanent settlements(D MA and δD)of slopes

4.3 邊坡主余震響應的預測

在上述相關性研究中，共探討了三類主余震強度參數與位移參數的相關性，結果表明：主震強度參數與邊坡主余震位移的相關性最強。基于篩選的兩個最優地震動強度參數Sa(Ts)M和ASIM，通過最小二乘回歸方法，建立兩個主余震位移預測模型(對數線性)。如圖12所示，所提出的位移模型能夠較好地描述數值模擬的結果。在已知主震反應譜加速度或主震加速度譜強度的情況下，可對主余震作用下的邊坡坡肩豎向永久位移DMA進行預測。需要指出的是，本文所建立的主余震位移預測模型僅針對算例邊坡，若邊坡土體參數或邊坡尺寸改變時，上述模型參數也應相應修改。

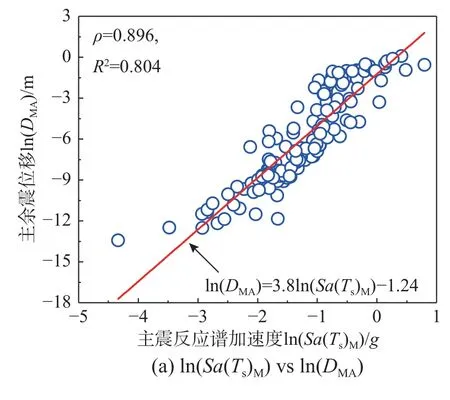
圖12 基于最優地震動強度參數的主余震豎向位移預測Fig.12 Predictive model for vertical permanent settlement of slopes based on optimal IM saspredictors.

5 結論

本文通過對邊坡在真實主余震序列作用下的大量位移響應進行分析，對余震對邊坡位移的影響開展了評估研究，同時探討了采用不同地震動參數表征的主余震序列強度與邊坡位移響應的相關性，得到如下結論：

(1)余震會對主震損傷邊坡產生較為明顯的增量損傷。在所挑選的210條真實主余震序列中，40.0%的主余震序列造成的位移增量比大于10%且小于100%；6.2%的余震作用下產生的位移甚至大于主震位移。

(2)主余震序列強度與邊坡主余震位移的相關性分析結果表明：主震強度與邊坡主余震位移的相關性最強。在所考慮的地震動強度參數中，與主余震位移參數相關性最強的兩個參數為主震反應譜加速度Sa(Ts)M與主震加速度譜強度ASIM。

(3)根據主余震序列強度與典型分層邊坡主余震位移的相關性，建立了兩個主余震位移預測模型，可以較好地預測算例邊坡的主余震位移響應。

本文的相關結果通過本文算例邊坡計算獲得，但相關規律并不局限于此算例邊坡，其同樣適用于其它具有不同幾何尺寸和土體參數的邊坡工況。由于地震序列本身的復雜性和邊坡動力響應的強非線性，對于邊坡的主余震反應特性還需要進一步深入研究來考慮不同場地條件、邊坡類型、土體參數等對邊坡位移結果的影響。此外，還需要開展一系列物理模型試驗研究，以加深對邊坡在主余震作用下破壞過程及其破壞機理的認識。