翻轉課堂教學模式在理論力學教學中的應用
——以平面簡單桁架的內力計算為例

張會領，吳光林，曾春華

（廣東海洋大學海洋工程與能源學院 廣東 湛江 524000）

傳統教學模式以教師為中心開展教學活動，學生在“課中學習，課后內化”。傳統教學模式可以實現知識的高效學習，但對知識內化的過程重視不夠。此外，傳統教學忽視學生在學習過程中的主體地位，不利于深度學習[1]。翻轉課堂是信息技術與教育深度融合后形成的一種教學模式。翻轉課堂將傳統的課堂教學內容前置，要求學生在課前通過自學完成基礎知識的學習，而將原本在課下進行的知識內化轉移到課中進行[2]。課中教學以問題為導向，以討論交流為主要方式，以知識的內化為主要目的。從理論上講，翻轉課堂教學模式可以充分調動學生的學習積極性，有效促進深度學習的發生，實現教學效果的提升[3]。翻轉課堂教學是對傳統教學模式的一種顛覆，它的出現勢必引發教師角色、教學思維模式、課堂管理模式和考核模式的改革[4]。本文以“理論力學”課程中桁架內力計算為教學案例，探討翻轉課堂教學模式在實際教學中的應用。

1 翻轉課堂教學模式設計

1.1 課前階段

教師根據教學內容和教學目標，選擇實施翻轉的知識點，收集教學資源，制作課前學習材料[5]。在推送學習任務之前，先給學生推送學習任務清單，明確學習任務和要求。課前學習材料要重點突出，目標明確，知識性和趣味性并舉，適合學生自學的特點。課前學習內容要保證每個初學者都能順利完成學習任務。學習資料的推送要注意節奏，學習內容與課后測試相關聯[6]。并且強調每個學生只有通過測試才算完成課前學習，否則需要重新學習相關內容。

1.2 課中階段

在此階段，老師與學生在課堂上討論交流，完成知識的內化，促進深度學習發生[7]。課中是翻轉課堂教學的關鍵，翻轉課堂教學的成敗在此一環。首先，課中教學要調動學生參與討論的積極性，這是開啟深度學習的前提。其次，教師要設計討論的話題和問題，采取問題驅動型教學。學生分組，采用頭腦風暴的方法進行討論，組與組之間可以交流，互相質疑和辯論。老師匯總課堂討論結果、問題和建議，并做出點評。最后，老師根據教學情況和學生反饋，改進教學中存在的不足。

1.3 課后階段

課后階段，老師根據學生在課堂上的表現設計復習題和思考題，這些題目是老師根據學生課堂上反饋內容所設計的[8]。題目分為復習題和思考題，復習題是學習內容的鞏固和練習，是教學內容的總結和能力提升訓練。思考題主要培養學生的創新思維，通過思考題的訓練，提高學生的鉆研能力，培養科學精神。

2 翻轉課堂教學案例

下面以“平面簡單桁架的內力計算”為例進行翻轉課堂教學設計，展示翻轉課堂在“理論力學”教學過程中的具體應用。

2.1 課前教學內容

2.1.1 桁架的基本概念和分類

通過橋梁和房屋的梁架引出桁架的概念（圖1），介紹桁架的組成，桁架的分類以及桁架結構在工程中的應用及其優點。利用桁架結點與桿數的關系對桁架進行分類，設總桿數用m 表示，總節點數用n 表示。簡單桁架：m=2n-3；復雜桁架：m＞2n-3。若m＜2n-3，則不是桁架[9]。

圖1 桁架結構的組成

2.1.2 關于桁架的幾個假設

為了簡化桁架的計算，對桁架進行如下規定：①桁架中各桿件均為直桿，各桿件軸線位于同一平面內，且各桿件軸線通過節點中心；②桁架中各桿件的兩端均為光滑鉸鏈連接；③桁架所受力都作用在節點上，而且在桁架的幾何平面內；④桁架桿件的重量不計，或平均分配在桿件兩端的節點上，也位于桁架的幾何平面內。

根據這些假設，組成桁架的桿均為二力桿。

2.1.3 平面簡單桁架的內力計算

介紹兩種計算簡單桁架內力計算的方法：節點法和截面法。

①節點法。先對桁架進行整體分析，求出作用在桁架上的約束力。然后，以每個節點為研究對象，可以列出2 個平衡方程。逐個節點進行分析，求出全部桿件的內力。節點法原理簡單，但計算過程卻比較煩瑣，主要用于桁架設計，通過例題講解節點法的應用。

②截面法。可以假想一個截面，把桁架截開，取桁架的一部分為研究對象，可以列3 個平衡方程，求出這些被截桿件的內力，這就是截面法。截面法一般用于桁架的校核。通過例題介紹截面法的應用。

2.2 課中學習

節點法和截面法常用來計算桁架的內力。但對于節點數較多的復雜桁架的內力計算這兩種方法都不太合適。復雜桁架的內力計算是通過零桿的判別進行簡化的。本次課中的教學活動圍繞零桿的判別展開，教學方法采用問題驅動式教學法（圖2）。

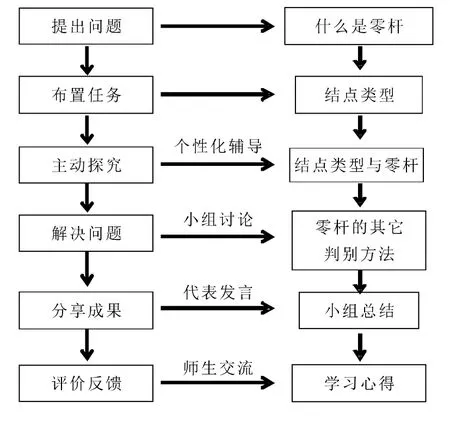
圖2 問題驅動型課中教學設計

2.2.1 什么是零桿

在某種荷載作用下軸力為零的桿件稱為零桿。零桿對保證桁架的幾何結構是不可或缺的。在桁架內力計算過程中，首先要判斷零桿。提出問題，讓同學找出桁架中的零桿（圖3），引出零桿的判別方法。

圖3 桁架結構中的零桿

2.2.2 節點類型與零桿的關系

桁架中零桿的識別一般是通過節點的結構形狀判斷的。在桁架中快速識別這些節點結構就能準確判斷零桿。常見的節點類型共有三種：“V”型節點、“T”型節點和“K”型節點。

①“V”型節點。“V”型節點由不共線的兩桿連接構成。如果節點不受外力作用，則兩桿皆為零桿；若其中一桿與外力共線，則不與外力共線的一桿為零桿（圖4）。

圖4 “V”型節點中的零桿

②“T”型節點。“T”型節點由三根桿組成，其中兩桿共線，不共線一桿為零桿，而共線的兩桿內力相等且性質相同（圖5）。

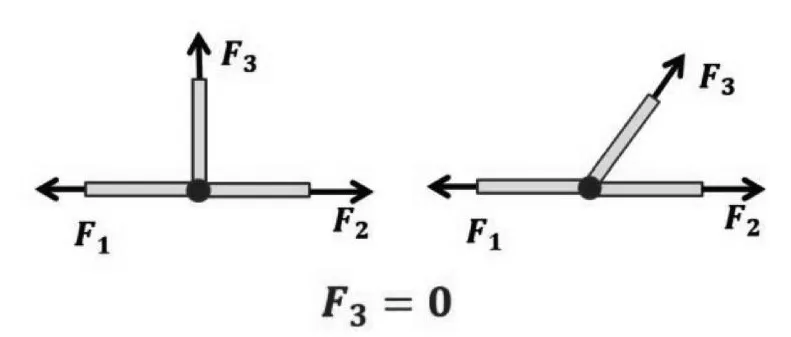
圖5 “T”型節點中的零桿

③“K”型節點。“K”型節點由四桿相交成對稱K 形，節點在無荷載作用時兩斜桿軸力等值異號。對稱桁架在對稱荷載作用下，對稱位置上的K 形節點若無荷載作用時，該節點上的兩根斜桿為零桿（圖6）。

圖6 “K”型節點中的零桿

以上幾個結論都可以用節點的平衡條件求出。

2.2.3 利用節點類型識別零桿

零桿判斷的關鍵是能夠在桁架中識別節點類型，并根據不同的節點類型完成零桿的識別。這是從知識向能力轉化的一個過程。在課堂上給出不同類型的桁架，讓學生判斷桁架中的零桿（圖7）。

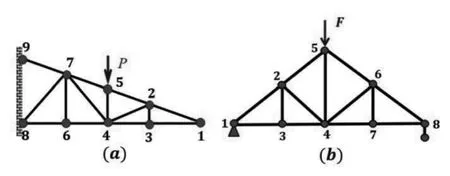
圖7 桁架結構中零桿的識別

經過小組討論，解決上面的問題。收集學生在分析過程中存在的問題，并給予解答。在圖7a 中節點1 是“V”型節點，所以桿12 和桿13 是零桿。可以假想去掉這兩根桿，則節點3 也是“V”型節點，桿34 和桿23 也是零桿。去掉這兩根桿，2 節點是“V”型節點，桿24 和桿25 是零桿。節點5 是“V”型節點的第二種類型，所以桿57 是零桿。節點6 是“T”型節點，所以桿67 是零桿。在圖7b 中，桁架結構及其受力左右對稱，4 節點是“K”型節點，所以桿24 和桿46 是零桿，節點3 和節點7 是對稱的“T”型節點，所以桿23 和桿67 是零桿。

2.2.3 其他方法判定零桿

利用節點類型可以快速判別零桿，但并不是所有的零桿都可通過節點類型分析找出來。接下來通過練習，讓學生探索其他判斷零桿的方法（圖8）。

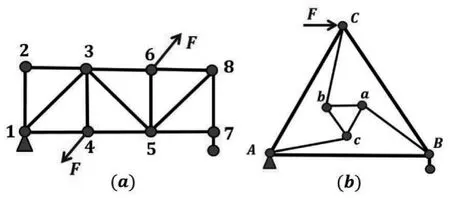
圖8 特殊外力作用下零桿的識別

在圖8a 中兩個大小相等方向相反的力分別作用在節點4 和節點6，相當于一個平衡力作用在桁架的局部上，而桿34、桿45、桿56、桿36 和桿35 也構成一個桁架，受力不變形，因此只有桿34、桿45、桿56、桿36 和桿35 有內力，組成桁架的其余桿件均不受力，都是零桿。這就是靜定結構的局部平衡特性：將一個平衡力系作用于靜定結構中幾何形狀不變的局部時，結構其余部分不產內力。

在圖8b 中，外力F 作用在C 點，滾動支座B 提供豎直向上的力，固定鉸鏈支座提供水平向左的力和豎直向下的力，在這三個力的作用下，整個桁架平衡，由于三角形具有穩定性，所以△ABC 內部的桿件并不會受到力的作用，都是零桿。這就是附屬結構的性質：作用在基本部分的力只使基本部分產生內力，作用在附屬部分的力卻能使附屬部分和基本部分產生內力[10]。

最后，讓各小組總結課堂討論的成果，并以課堂發言的形式進行交流，與大家分享學習心得體會。老師在各小組發言后進行點評，總結桁架零桿判斷的規律，并收集學生對課堂的意見和建議，進一步優化教學設計。

2.3 課后拓展學習

零桿判斷是桁架計算的重要內容。判斷零桿的方法有很多，需要同學們在掌握基本的零桿判斷技巧的基礎上靈活運用，才能達到事半功倍的效果。課后給同學們布置思考題，鞏固學習內容（圖9）。

圖9 課后拓展練習

根據學生課后反饋情況，在學習平臺推送思考題的分析過程：在圖9a 中節點E 為“V”型節點的第一種類型，所以桿EF 和桿EC 為零桿。節點G 和節點C 為“T”型節點，所以桿GD 和桿CD 為零桿。分析整體受力，B 點約束力豎直向上，B 節點為“V”型節點的第二種類型，所以桿AB是零桿。A 點的約束力豎直向上，不存在水平力，A 節點為“V”型節點的第二種類型，桿AD 為零桿。在圖9b 中，選擇一個通過桿EF 的截面將桁架上下截斷，對桁架上半部分進行受力分析，在水平方向上只有EF桿斷開后的內力，因此EF 桿為零桿。分析節點E，E 屬于“V”型節點的第一種類型，所以桿AE 和桿BE 都是零桿。分析B 節點，屬于“V”型節點的第二種類型，所以桿AB 為零桿。

3 結語

翻轉課堂在“理論力學”中的應用彌補了傳統教學模式的不足，以問題驅動的翻轉教學模式提升了教學效果，促進了學生深度學習的發生。值得注意的是，翻轉課堂對教師和學生都提出了更高的要求。教師作為翻轉課堂的“導演”要創新翻轉課堂教學內容，采用合理的激勵機制，培養學生自主學習的良好習慣，營造良好的課堂氛圍，驅動深度學習的發生。對學生而言，翻轉課堂要求學生轉變學習態度，實現從“要我學”到“我要學”的轉變。因此翻轉課堂教學要充分調動學生的積極性，提高學生在課前階段學習的自覺性和課中討論的參與度以及課后思考的開放性，這是提升翻轉課堂教學效果必須考慮的問題。