HPM視角下“等比數列的前n項和公式”的教學*

宜賓學院人工智能與大數據學院 (644000) 覃 淋

巴中職業技術學院教育學院 (636000) 喻曉婷

1 引 言

《普通高中數學課程標準(2017)》在“教材編寫建議”中指出，“要體現數學內容的邏輯體系，揭示數學內容的發生、發展過程……創設合適的問題情境，設計有效的數學學習活動，展示數學概念、結論、應用的形成發展過程．”數學史作為數學教學的重要資源，數學史的教育價值也得到了理論與實踐兩個層面的普遍認同．美國數學史家卡約里(FlorianCajori，1859-1930)認為“數學史是使面包和黃油更加可口的蜂蜜”，在其著作《AHistoryofMathematics》(1926)中指出：“如果用歷史軼事點綴枯燥的計算和證明，學生的興趣就會大大增加．…… 通過對數學歷史的介紹，能夠讓學生明白數學并不是一門呆板乏味的學科，而是一門不斷進步且生動有趣的學科.”有學者從概念、文化、動機三個層面討論了數學史的教育價值，指出數學史具有幫助學生拓寬視野、增加興趣、創造學習動機、促進學生思考等教育價值．數學史融入課堂教學的實踐表明，數學史具有知識之諧、方法之美、探究之樂、能力之助、文化之魅、德育之效等多元的教育價值和文化價值．

“等比數列的前n項和”是人教A版高中數學選擇性必修二第4章《數列》4.3節的內容，是“等差數列”內容的延續，是進一步學習數列知識和解決一類求和問題的重要基礎和有力工具．等比數列模型在實際生活中有著廣泛的應用，蘊含了一些重要的數學思想方法．《普通高中數學課程標準(2017)》中要求學生“探索并掌握等比數列的前n項和公式，理解等比數列的通項公式與前n項和公式的關系．”

本文通過選取歷史上的素材，設計一系列問題，將數學史上不同地區、不同民族關于等比數列求和公式的多種推導方法融入課堂教學，讓學生了解數學知識的發生發展的歷程，感受數學的文化多元性，領略數學文化的魅力，形成動態的數學觀，發展學生的數學核心素養；并通過數學史融入課堂教學，培養學生對數學積極的情感態度，營造人性化的課堂，在潛移默化中實施數學學科德育，落實立德樹人根本任務．

2 教學設計與實施

2.1 創設情境，呈現問題

首先引導學生復習前面學習的等差數列的定義、通項公式、前n項和公式及等比數列的通項公式等內容．然后提出19世紀初，美國數學家亞當斯(D.Adams，1773-1864)的著作《學者算術》中的妻子問題：我赴圣地伊夫斯，路遇一男攜七妻，一妻各自負七袋，每袋都裝七貓咪，貓咪又把七仔生，同去圣地共幾何？

對于這個問題，學生很容易想到把每項算出來，再相加．接著教師再用PPT呈現“棋盤問題”，教師再向學生提問，“如何計算棋盤上的麥粒總數？”

在學生交流討論的同時，教師播放制作的微視頻介紹等比數列求和問題的歷史以及歷史上一些著名的等比數列求和問題．

2.2 合作交流，探究規律

教師通過課前制作的微視頻，介紹等比數列求和公式推導的可能思路．引導學生分小組進行探究．小組討論后，請各組代表分別上臺展示．

小組一：(錯位相減法)利用錯位相減法推導公式，學生的思路如下：

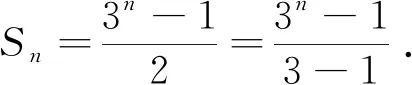
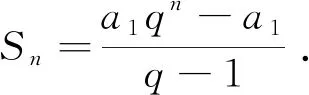
小組二：(古埃及的方法)由等比數列的定義，找到前n項與前n-1項的關系，得到二者的等量關系，學生思路如下：

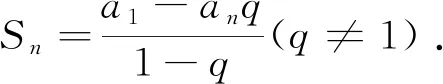
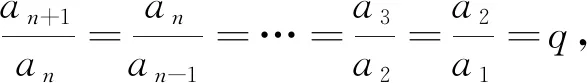
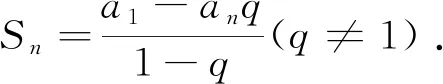
小組六：(幾何推導法之一)假設等比數列首項a1>0，公比為q>0，學生的推導思路如下：

如圖1，在一個正切值為公比q的直角三角形中，在底邊作出長度為a1的線段，再作垂線段交于斜邊，那么垂線段的長度為a2=a1q；再從交點出發，作長度為a2的與底邊平行的線段，然后再向上作垂線交于斜邊，則垂線段的長度為a3=a2q；以此類推，直到第n-1步，作長度為an-1的與底邊平行的線段，然后再向上作垂線交于斜邊，則垂線段的長度為an=an-1q．底邊的長度為a1+a2+…+an-2+an-1，另一直角邊的長度為a2+a3+…+an-1+an．從而有q=

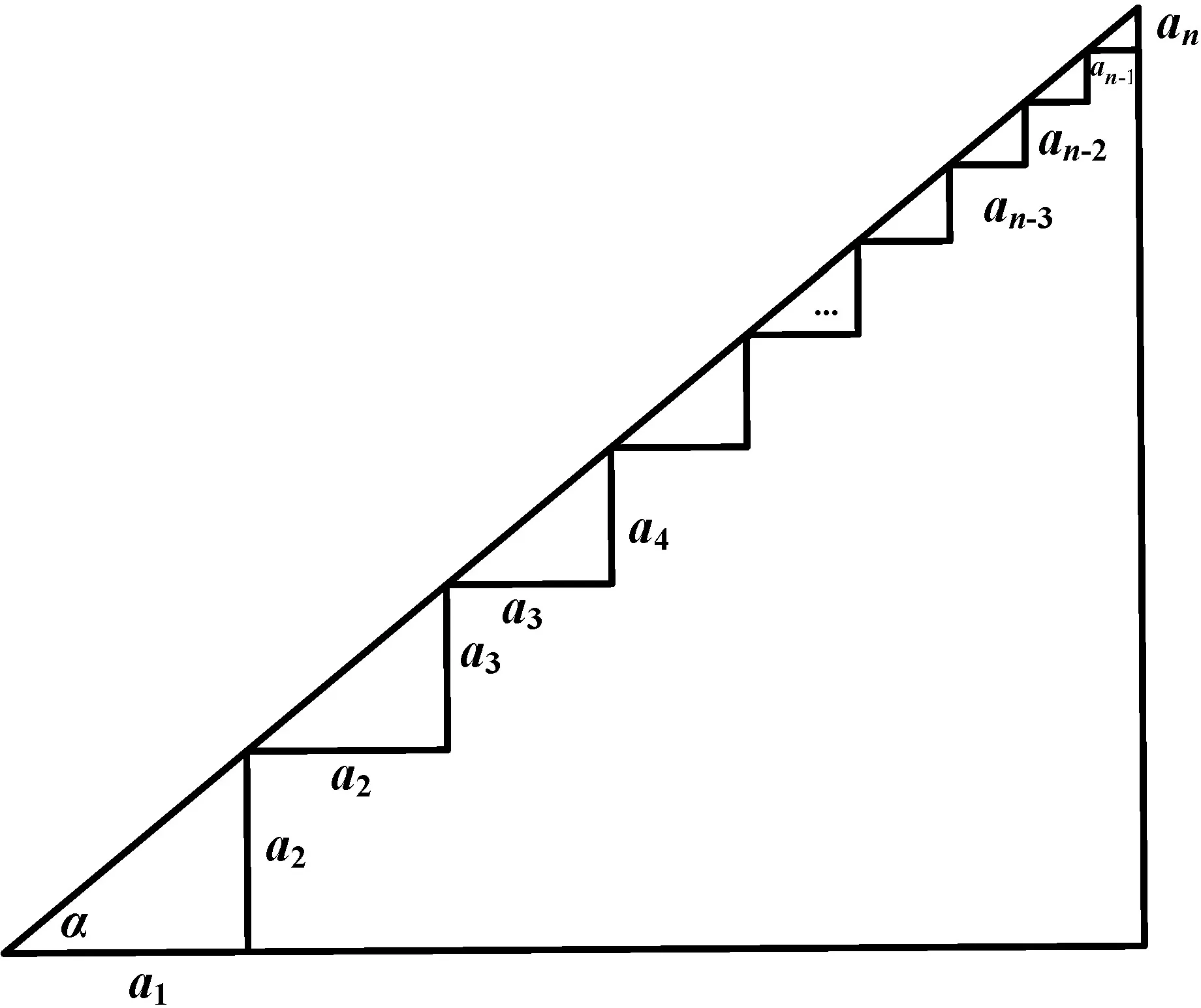
圖1

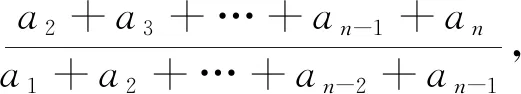
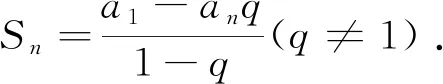
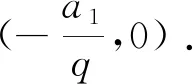
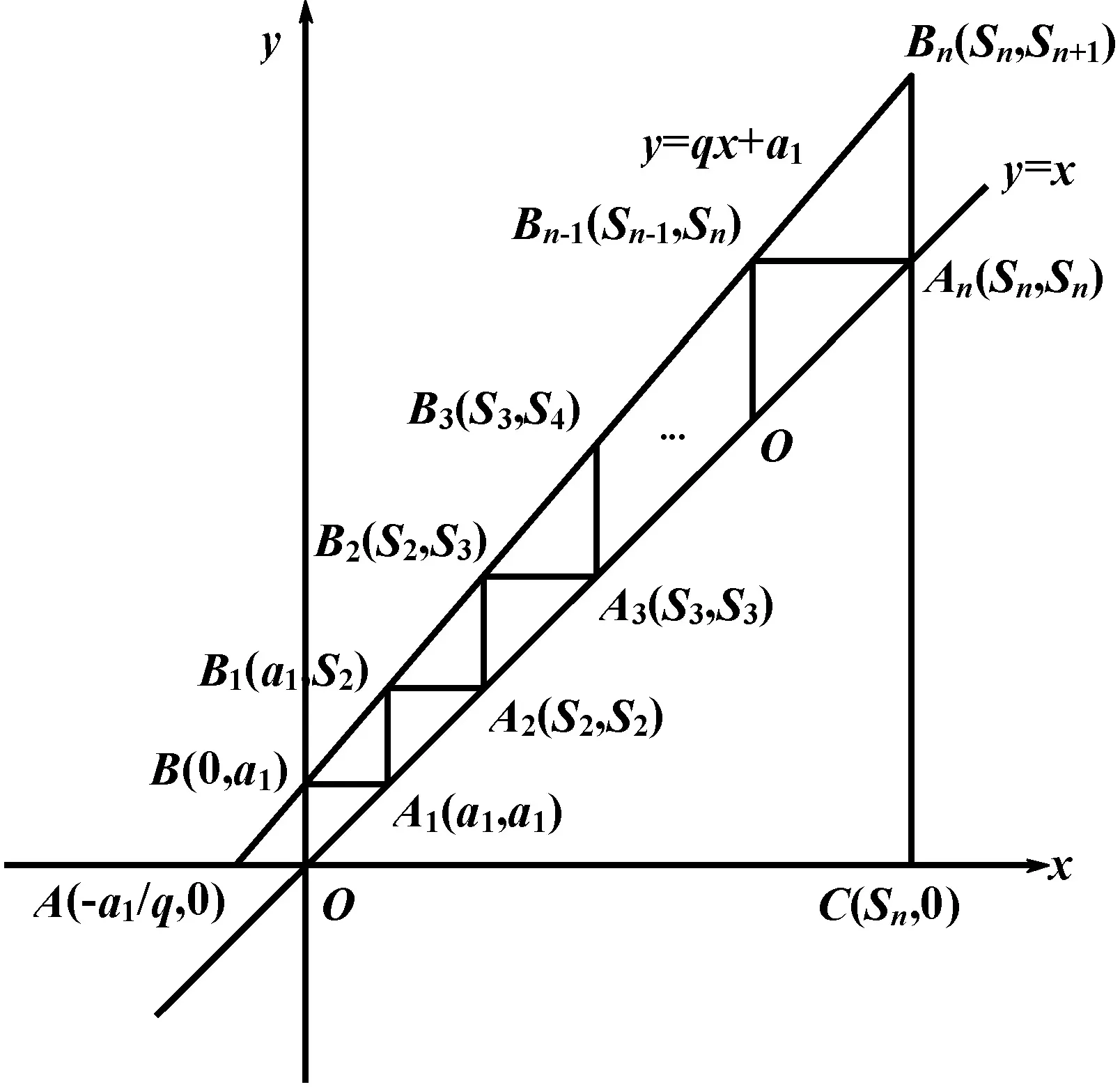
圖2

2.3 教師總結規律

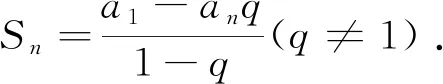
2.4 應用規律

隨后，教師要求學生利用求和公式解決一些問題，體會數學的實用性．

問題1 某國王征兵，規定第一個村子征兵1人，第二個村子征兵2人，第三個村子征兵4人，第四個村子征兵8人，以此類推，直到第三十個村子，問：一共征兵多少人？(阿爾昆《敏銳青年之命題》)

問題2 今有出門，望見九堤，堤有九木，木有九枝，枝有九巢，巢有九禽，禽有九雛，雛有九毛，毛有九色．問共幾何？(《孫子算經》)

問題3 遠望巍巍塔七層，紅燈點點倍加增．共燈三百八十一，請問尖頭燈幾盞？(《算法統宗》)

2.5 總結提升

本節課學習了等比數列的前n項和公式，從古巴比倫泥版上的分財產問題，經歷了古埃及人、《幾何原本》、印度數學家、中世紀歐洲數學家，再到歐拉《代數學基礎》中的錯位相減法，領略了歷史上等比數列求和公式的不同精彩證法．同學們在本節課中學習了多種數學思想方法：特殊到一般的思想、方程的思想、數學結合的思想、分類討論的思想，同時也培養同學們的數學抽象、數學運算、直觀想象、邏輯推理以及數學建模等數學核心素養．并且通過對不同文明中等比數列求和公式的不同推導方法的介紹，讓我們多了一個觀察角度，多了一種表達方式，多了一種研究手段．

3 學生反饋

課后，對全班41名學生進行問卷調查．80%的學生聽懂了本節課的內容，極少部分基礎較差的學生覺得本節課課堂容量有些大．95%的學生喜歡本節課中數學史融入課堂的教學方式，希望老師在以后的教學中也多采用這樣的方式進行教學．

學完本節課后，學生會想到的關鍵詞有：巴比倫泥版、紙草書、《孫子算經》、《幾何原本》、《算法統宗》、歐拉、數學文化、數學史等．

關于本節課中印象最深的內容，學生的典型回答有：古埃及人的計算方法非常巧妙，但我們也不能完全局限于他們的思路；歷史讓人穿越迷霧，感受到了數學的脈動；解決同一問題常常有不同的方法，讓人大開眼界；歷史上的數學問題很有意思，很多公式的發明創造，都是數學家為了解決實際問題的而創造的；數學公式并不是憑空產生的；數學文化博大精深，中國古代數學家在數學上也做出了很大貢獻．

學生的這些回答，正如法國數學教育家J.Swetz所言：“在數學問題求解中可選取歷史上不同時期、不同文化的一些數學名題．這些名題及其解答提供了實質性的數學思想方法，并蘊含了數學家為之奮斗的曲折歷程與苦樂體驗，展現了生動而廣闊的人文背景．”

關于本節課中等比數列的前n項和問題的歷史印象對數學學習的幫助和啟示，學生的典型回答有：今天一節課的內容是古人幾千年智慧的結晶；數學史、歷史數學名題既可以增加課堂的趣味性，又可以幫助記憶、理解公式；學習數學家不畏艱險、刻苦專研的精神；課堂上應該多介紹一些關于數學知識的歷史，擴充背景有利于數學學習；數學史讓數學變得有意思；同一個問題，從不同的思路出發，都可以解決問題．

課后訪談表明，學生對于第一次在數學課堂中深入接觸數學史，感覺比較新鮮，知道了等比數列求和問題古已有之，通過對數學發展史的了解，感受到了數學史對自己數學學習的幫助，并且認為數學史的融入活躍了課堂氣氛，增加了課堂的趣味性，也激發了學習興趣．同時也認識到數學與不同的學科之間都有著密切的聯系．在課堂教學中，數學史為學生提供了許多探究的機會，讓學生可以在教師的引導下經歷“火熱的思考”，變為“數學家”，把數學“再創造”出來．學生在這樣的學習過程中，既拓寬了視野，又體會了“再創造”數學的喜悅．

4 結 語

等比數列的前n項和公式是高中數學的重要內容，教材中介紹的“錯位相減法”具有較強的技巧性，如無教師引導，學生很難想到．對學生而言，這樣的知識是不“自然”的．我們基于HPM的視角，設計課堂教學，從學生已有知識結構出發，創設問題情境，引起認知沖突，搭設“腳手架”，使得公式的產生變得自然，揭示了數學知識之諧；通過古今方法的比較，呈現了數學方法之美；將歷史與現實相聯系，同時為學生提供了探究的機會，讓學生體驗了探究之樂；以故事的形式讓學生用所學知識解決問題，培養了學生解決問題的能力，達成了能力之助．通過對不同文明中等比數列求和問題的介紹，凸顯人文元素，將歷史與現實、數學與人文、數學與科學聯系起來，通過歷史把數學的“學術形態”轉化為“教育形態”，降低了學生數學學習的外在認知負荷．既培養了學生的多元文化視角，又滲透了數學文化，展示了數學文化的魅力．通過等比數列求和公式不同時期的不同推導方法的介紹，讓學生明白數學是不同時期數學家共同努力的智慧成果，培養學生獨立思考、敢于質疑、追求創新的理性精神，達成了德育之效．