一類條件最值問題的快速解法*

福建省龍巖市高級中學 (364000) 李桂英

基本不等式是求解函數最值問題的一個有效工具，不僅是高中數學教學的重點，而且是高考考查的一個熱點.然而，學生在應用基本不等式求最值時，往往因為不知如何獲取“和為定值”或“積為定值”導致無法運用基本不等式正確求解出最值.而靈活應用已知條件去構造、去變形從而獲得“定值”又是此類問題的難點.針對學生不能靈活獲取“定值”的實際，筆者在教學實踐中，探尋了一種既能降低構造“定值”這個難點，同時又能快速準確求出一類條件最值問題，本文將結合教學實踐，例說此類條件最值問題的快速解法.

1 一個重要結論

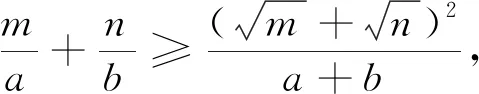
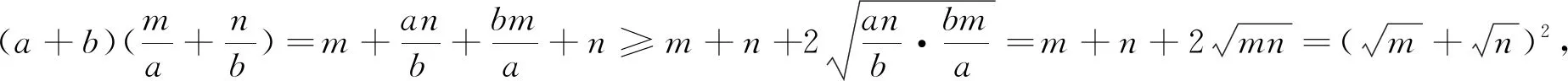
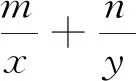
此類條件最值問題的常規解法是通過常值代換后利用基本不等式來求解.若能靈活應用本文定理求解，便可避免常值代換，使此類問題直接快速得到求解.

2 應用

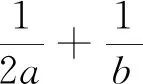
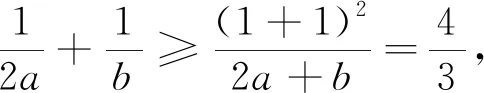
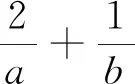
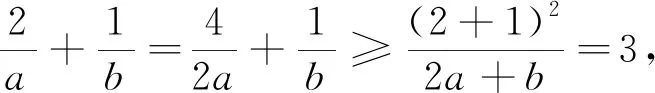
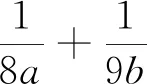
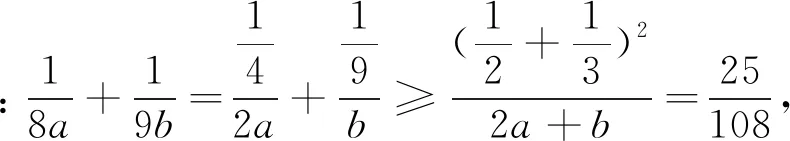
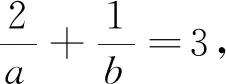
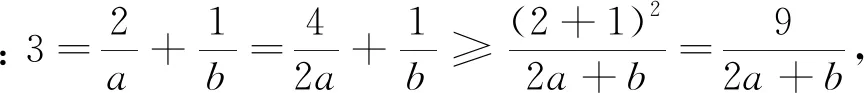
變式4 已知a>0,b>0，且2a+b=3ab，求2a+b的最小值.

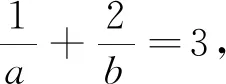
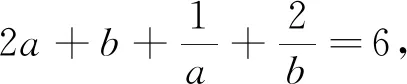
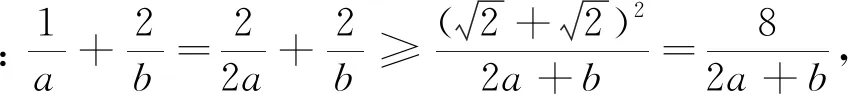
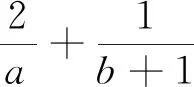
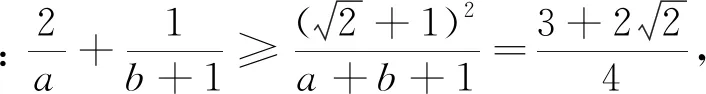
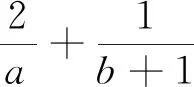
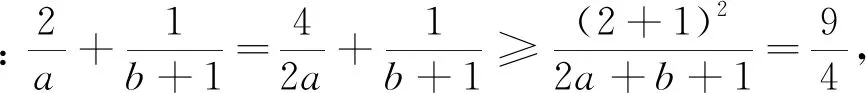
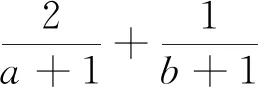
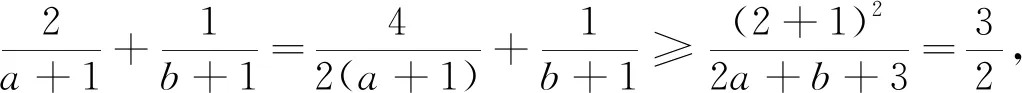
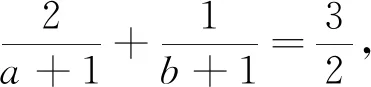
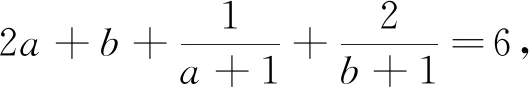
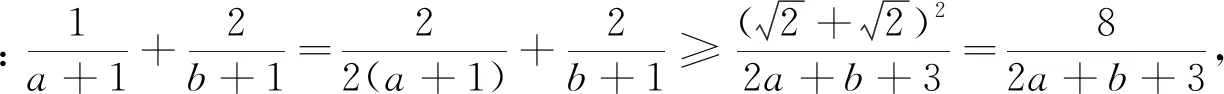
綜上可見，引導學生嘗試應用本文中所推證的結論去求解一些條件最值問題，不僅能很大程度上降低了構造定值的難度，減少了計算量，從而縮短了學生解決此類問題所耗費的時間，有效地提高了學生解題的準確率，而且能很好地滲透了化歸與轉化的重要數學思想.并且通過一題多變，多題歸一，能加深學生對定理本質的理解與掌握，達到對此類題目的融會貫通.