圓錐曲線綜合測試卷(A 卷)答案與提示
2023-04-25 16:31:36
中學生數理化(高中版.高二數學) 2023年5期
一、選擇題
1.C2.D3.A4.D5.B
7.B 提示:設橢圓的左焦點為E,連接AE,BE。因為AF⊥BF,所以四邊形AEBF為矩形,∠EAF=90°,∠ABF=∠AEF,|AF|=2csinα,|AE|=2ccosα。
8.D 提示:假設A在第一象限,如圖1。
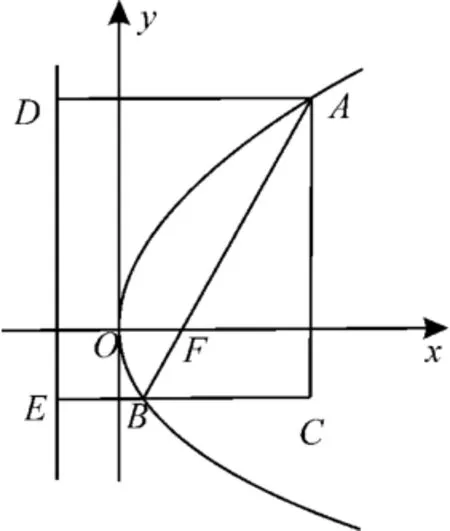
圖1
過A,B分別向拋物線的準線作垂線,垂足分別為D,E。
過A作EB的垂線,垂足為C,則四邊形ADEC為矩形。
由拋物線定義可知|AD|=|AF|,|BE|=|BF|。
又因為|FA|=3|FB|,所以|AD|=|CE|=3|BE|,即B為CE的三等分點。
設|BF|=m,則|BC|=2m,|AF|=3m,|AB|=4m。
10.D 提示:如圖2 所示,分別過點A,B作準線的垂線,垂足分別為E,M,連接EF。拋物線C的準線交x軸于點P,則|PF|=p。由于直線l的斜率為,故其傾斜角為60°。又AE∥x軸,故∠EAF=60°。由拋物線的定義可知,|AE|=|AF|,則△AEF為等邊三角形,∠EFP=∠AEF=60°,∠PEF=30°。所以|AF|=|EF|=2|PF|=2p=8,解得p=4,故A正確。
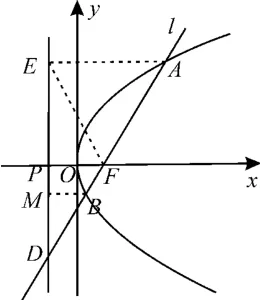
圖2
因為|AE|=|EF|=2|PF|,PF∥AE,所以F為線段AD的中點,則故B正確。
因∠DAE=60°,故∠ADE=30°,|BD|=2|BM|=2|BF|(拋物線定義),故C正確。
因為|BD|=2|BF|,所以|BF|=,D 錯誤。
11.B 提示:由題意可知,直線l的方程
二、填空題
16.④
提示:設P(x0,y0),過點P與AB平行的直線為l。
要使△ABP的面積最大,只需點P到AB的距離最大。
而P點是拋物線的弧AOB上的一點,故點P是拋物線上平行于直線AB的切線的切點。
三、解答題
猜你喜歡
語數外學習·高中版上旬(2024年18期)2024-02-20 00:00:00
中學生數理化(高中版.高二數學)(2022年1期)2022-04-26 13:59:56
中學生數理化·中考版(2021年10期)2021-11-22 07:26:38
海峽姐妹(2020年9期)2021-01-04 01:35:44
VOGUE服飾與美容(2020年9期)2020-09-02 14:47:26
中學生數理化·中考版(2019年10期)2019-11-25 09:39:04
中學生數理化·中考版(2017年10期)2017-04-23 06:29:38
中學生數理化(高中版.高二數學)(2017年1期)2017-04-16 05:33:44
山東青年(2016年1期)2016-02-28 14:25:25
當代修辭學(2014年3期)2014-01-21 02:30:44

