成對數據的統計相關性高考題型剖析

■甘肅省白銀市第一中學 胡貴平

定性和定量分析成對數據的統計相關性是統計學中的重要內容,也是高考的熱點,現對高考中常見題型進行剖析,歸納整理。

一、散點圖判斷相關關系

例1(2020年全國Ⅰ卷理科數學)某校一個課外學習小組為研究某作物種子的發芽率y和溫度x(單位:℃)的關系,在20 個不同的溫度條件下進行種子發芽實驗,由實驗數據(xi,yi)(i=1,2,…,20)得到如圖1的散點圖。

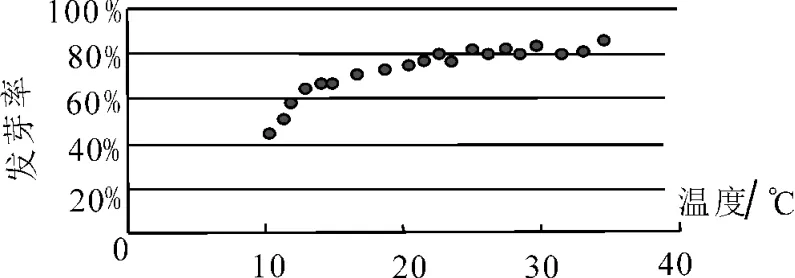
圖1

由此散點圖,在10℃至40℃之間,下面四個回歸方程類型中最適宜作為發芽率y和溫度x的回歸方程類型的是( )。

A.y=a+bxB.y=a+bx2

C.y=a+bexD.y=a+blnx

解析:由散點圖分布可知,散點分布在一個對數函數的圖像附近,因此,最適合作為發芽率y和溫度x的回歸方程類型是y=a+blnx。故選D。

二、一元線性回歸方程模型

(1)求家庭的月儲蓄y關于月收入x的線性回歸方程y=bx+a;

(2)判斷變量x與y之間是正相關還是負相關;

(3)若該居民區某家庭月收入為7千元,預測該家庭的月儲蓄。

故所求回歸方程為y=0.3x-0.4。

(2)由于變量y的值隨x值的增加而增加(b=0.3＞0),故x與y之間是正相關。

(3)將x=7代入回歸方程,可以預測該家庭的月儲蓄為y=0.3×7-0.4=1.7(千元)。

例3(2014年新課標Ⅱ卷理數改編)某地區2007年至2013年農村居民家庭人均純收入y(單位:千元)的數據如表1所示。

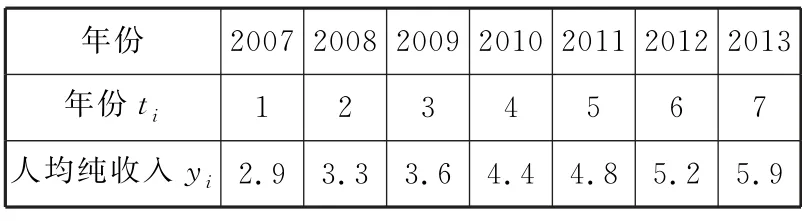
表1

(1)求y關于t的線性回歸方程;

(2)利用(1)中的回歸方程,分析2007年至2013年該地區農村居民家庭人均純收入的變化情況,并預測該地區2023年農村居民家庭人均純收入。

所以y關于t的回歸方程為y=0.5t+2.3。

(2)因為b=0.5＞0,所以2007 年至2013年該區人均純收入穩步增長,每年增加0.5千元。預計到2023年該區人均純收入y=0.5×17+2.3=10.8(千元)。因此,預計到2023年該區人均純收入約10.8千元。

三、一元線性回歸方程性質

例4(2014年湖北文數)根據如下樣本數據(表2)得到的回歸方程為=bx+a,則( )。

表2

A.a＞0,b＜0 B.a＞0,b＞0

C.a＜0,b＜0 D.a＜0,b＞0

解析:作出散點圖,如圖2所示。

圖2

故選A。

例5(2013年福建文數)已知x與y之間的幾組數據如表3所示。

表3

圖3

四、相關系數r

例6(2017全國新課標Ⅰ卷文數)為了監控某種零件的一條生產線的生產過程,檢驗員每隔30 min從該生產線上隨機抽取一個零件,并測量其尺寸(單位:cm)。表4是檢驗員在一天內依次抽取的16 個零件的尺寸。

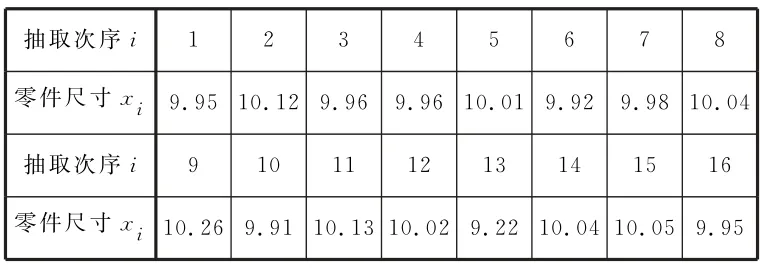
表4

(1)求(xi,i)(i=1,2,…,16)的相關系數r,并回答是否可以認為這一天生產的零件尺寸不隨生產過程的進行而系統地變大或變小(若|r|＜0.25,則可以認為零件的尺寸不隨生產過程的進行而系統地變大或變小)。

(i)從這一天抽檢的結果看,是否需對當天的生產過程進行檢查?

由于|r|＜0.25,因此可以認為這一天生產的零件尺寸不隨生產過程的進行而系統地變大或變小。