重型載貨汽車長下坡制動工況辨識

史培龍 高藝鵬 張子豪 趙軒 余強

關鍵詞：汽車工程；重型載貨汽車；制動工況；Markov-MonteCarlo方法；工況辨識；滾動時間窗

傳統持續制動系統的開啟和關閉主要依靠駕駛人的主觀判斷和操作，由于疲勞駕駛或路況不熟悉等因素影響，重型載貨汽車在下坡行駛過程中過度依賴行車制動系統而引起整車熱衰退問題，因此有效識別車輛的行駛狀態為車輛控制提供決策依據對于提高行駛安全性有重要意義。車輛的行駛工況能夠表征特定車輛在某種交通環境中的運行狀態[1]，但是傳統的汽車行駛工況用于新能源汽車的能量管理，未考慮山區公路車輛行駛特性。為了實現持續制動系統主動控制，有必要開展重型載貨汽車長下坡制動工況構建及辨識方法研究，為持續制動系統介入或退出決策提供依據。

關于行駛工況的構建，國內外相關學者做了不少研究，并取得了一定成果。為了反映車輛在真實道路下行駛狀態，速度、加速度[2-3]通常作為重要參數用于構建工況，一些學者[2]考慮了交通流帶來的影響，選擇城市、環路、鄉村、高速路段等不同等級的道路建立循環工況；一些學者考慮到城市地理特征因素，建立了典型城市（如西安[3]、呼和浩特[4]、大連[5]等）循環工況。但是，建立工況目的均用于混合動力汽車或純電動汽車的能量管理，車型多針對乘用車或城市客車。通過片段劃分[6]、主成分分析等數據處理后，運用Markov-MonteCarlo[7]、Multi-dimensionalMarkov鏈[8]、多島遺傳算法（multi-islandgeneticalgorithm）[9]、兩階段聚類等方法建立相應工況。上述參數及方法構建的工況未含道路坡度信息和制動踏板動作特性數據，不能夠準確反映山區道路車輛行駛狀態特征。

工況辨識方面，目前有遺傳混合整數優化算法[10]、模擬退火算法[11]、PSO-SVM算法[12]等用于工況辨識，但是用于構建工況的數據未考慮山區公路車輛行駛特性。余強等[13]提出了幾種制動方式聯合制動的智能控制方案，但是未對持續制動系統介入和退出方法展開研究；韓云武等[14-15]提出了輔助制動系統平滑進入與退出的控制策略，但是僅針對新能源汽車；利用坡度參數能夠實現自動控制，但是道路坡度大小和長度是隨機，且不同的駕駛人駕駛風格差異性較大，該方法適用性較差。

基于以上研究狀況和存在問題，本研究依托京昆高速雅安-西昌段典型山區路況試驗，提出包含制動踏板狀態、道路特征和車輛行駛狀態參數的重型載貨汽車長下坡制動工況構建及基于滾動時間窗的神經網絡辨識方法，構建適用于重型載貨汽車山區道路的制動工況和辨識模型，為重型載貨汽車長下坡制動電氣化智能控制提供依據。

1長下坡制動工況構建

1.1制動短行程定義與劃分

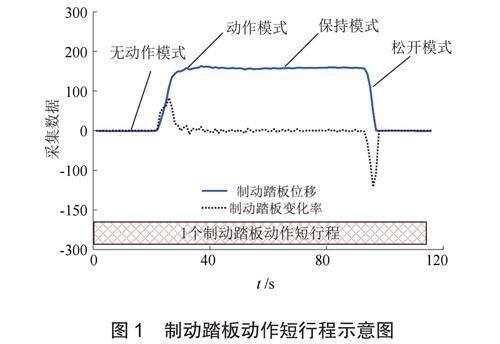
傳統循環工況中短行程通常是指從車輛運行的一個怠速時刻開始到下一個怠速開始時刻之間的運行過程[5]。由于重型載貨汽車在長下坡道路行駛時，車輛長時間處在運行狀態，傳統短行程不能詳細體現其制動情況。為拓展工況所包含的車輛運行狀態信息，基于傳統工況構建中短行程的定義，根據車輛制動行為，本文定義重型載貨汽車在長下坡道路運行過程中，從一個制動踏板無動作狀態開始到下一個制動踏板無動作狀態開始的行駛過程為一個制動短行程，即一次完全制動行為，稱“制動踏板動作短行程”，如圖1所示。一個制動踏板動作短行程同樣包含4種模式，具體如表1所示。

本研究基于京昆高速雅安―西昌段典型山區路段車輛道路試驗數據開展制動工況構建方法研究，試驗路段左線和右線全長約298km，垂直落差將近1600m，大于2%縱向坡度道路占58.14%，大于3%縱向坡度道路占27.49%，屬于典型的山區長大下坡路段，道路線型統計見圖2。試驗過程實時獲取制動踏板動作參數和車輛運行狀態參數。

按照制動踏板動作短行程定義，對試驗數據進行劃分，并剔除其中上坡制動踏板異常動作等無效短行程，共得到51條制動踏板動作短行程數據。

1.2狀態分類

1）片段劃分。以片段為數據單位合成工況可以區分道路類型，規避一個制動踏板動作短行程中不同時刻坡度出現較大變化的問題。將制動短行程劃分為制動踏板無動作模式、動作模式、動作保持模式、松開模式4種數據片段。依照圖3所示流程，共得到866個片段。

2）特征參數選取。車輛下坡行駛過程中，運行速度、制動踏板位移和道路坡度存在強烈的非線性關系，為此文中選擇制動踏板位移、坡度和速度參數，通過該參數的特征參數對狀態片段進一步劃分，相應特征參數如表2。

3）狀態分類。為了構建車輛行駛工況，文中對數據片段進行狀態分類。針對制動踏板、坡度和速度數據的不同特點，采用不同的方法進行聚類。針對制動踏板動作，首先利用制動踏板位移變化率和制動踏板位移參數進行主成分分析，再進行K聚類，設置聚類數為4，聚類結果如圖4。狀態1為低制動踏板位移，保持制動狀態；狀態2為中制動踏板位移，施加制動狀態；狀態3為中制動踏板位移，解除制動狀態；狀態4為高制動踏板位移，保持制動狀態。

對于坡度特征，由于單個片段時長較短，僅根據片段平均坡度，設置不同步長的區間，對坡度進行分類。設置坡度狀態數為3，即小坡度0～2.5%、中坡度2.5%～4.5%、大坡度4.5～6%。分類結果如圖5。

考慮到車輛行駛速度變化與制動強度、坡度等因素相關，通過平均速度vm等8項特征參數進行主成分分析，并利用主要特征參數進行狀態聚類，設置聚類數為4，聚類結果如圖6。狀態1為低速勻速行駛；狀態2為加速行駛；狀態3為減速行駛；狀態4為高速勻速行駛。

4）片段狀態求解。當前車輛行駛片段t的制動踏板位移狀態為Ds（t），坡度狀態為is（t），速度狀態為vs（t），根據文獻[4]中的編碼方式，由當前車輛行駛片段t的Ds（t）、is（t）、vs（t）獲得當前片段的編碼值。

其中：KD制動踏板位移狀態數；Ki：坡度狀態數。根據式（1），共有48個片段狀態，編碼狀態部分如表3。

5）狀態轉移概率矩陣。車輛從某時刻狀態變化到下一時刻某一狀態的過程稱為狀態轉移。對于車輛行駛片段構成的Markov過程，全部片段狀態之間的一步轉移概率組合形成狀態轉移概率矩陣P，如式（2）。

其中，pij表示從片段狀態i一步轉移至片段狀態j的狀態轉移概率。

本文對48個狀態的片段以及相鄰2個片段的狀態關系進行統計，根據出現的頻率計算概率，得出不同狀態之間的轉移概率為

其中，Nij為片段狀態從狀態轉移到狀態j的頻數，pij為從狀態i轉移至狀態j的轉移概率。

根據式（2）和（3）獲得3個參數運行工況片段的狀態轉移概率矩陣，其二維投影如圖7所示。ct表示當前行駛片段狀態，ct+1表示下一行駛片段狀態。實心圓的大小表示當前行駛片段狀態ct轉移到下一時刻狀態ct+1的概率。根據車輛運行特點，車輛行駛時保持自身狀態及其向相鄰狀態轉移的概率最大，沿著狀態轉移概率矩陣二維投影圖45°角平分線上分布。

1.3制動工況構建

重型載貨汽車長下坡制動過程中，制動踏板動作、道路坡度與車速變化存在明顯的因果關系，前一片段特征參數與后一時刻片段狀態變化具有明顯的時序性關系。但是，后一時刻片段的狀態取決于當前時刻的狀態，車輛在長下坡制動時，制動踏板位移從零開始，即車輛制動時制動踏板位移是從無動作狀態開始然后到動作狀態，或者繼續保持無動作狀態，因此，Markov理論在起始片段的確定上存在一定的欠缺。為此文中采用Markov-MonteCarlo模擬的方法克服先驗不足的問題，以車速平均值為依據，選擇與其差的絕對值最小的片段作為起始片段，坡度起始片段不予考慮。

運用Markov-MonteCarlo模擬方法生成符合狀態轉移概率矩陣的隨機數組，由此來確定后續狀態，并在對應片段集合選取最合適片段作為下一最優片段。具體過程為：設片段共有n個狀態，當前狀態為i，下一狀態為j，則從狀態轉移至狀態j的概率為Pij。狀態轉移矩陣的性質可知其每一行概率和為1，即式（4）

利用MATLAB中rand函數命令生成[0，1]之間符合均勻分布的隨機數x，如果隨機數符合式（5），則下一狀態就為k。將所屬狀態k的片段中，依據制定規則確定下一最優片段，并給k賦值i。重復步驟合成工況，直到達到設定的總時長。

以制動踏板位移、坡度和速度下一片段首位點與當前片段末位點差值絕對值之和最小值確定最優片段，如式（6），記錄其位置標號，并將其從片段集中剔除，以防止重復選擇片段。

其中：Dt+1，it+1，Vt+1分別為制動踏板位移、道路坡度、速度下一片段首位點，Dt，it，vt分別為制動踏板位移、道路坡度、速度當前片段首位點，asum為絕對值之和。

重復上述過程，直至工況長度滿足設定時長且最終制動踏板位移為零，完成一條候選工況構建，重復上述過程完成一定數量的候選工況構建，構建流程如圖8。本文共構建100條時長為1200s的重型載貨汽車長下坡制動工況。

2.1Markov特性

Markov過程是典型的隨機過程，具有“無后效應”。假設X是隨時間t變化的連續隨機過程，下一狀態Xt+1只與當前狀態Xt有關，與當前狀態之前的其他狀態無關。“無后效應”的強弱用相關系數表示。對于一個狀態序列{X}，長度為L，取{X}中[1：L-k]個狀態分量構成新狀態序列{X1}，取{X}中[k-1：L]個狀態分量構成新狀態序列{X2}。當狀態轉移間隔k較小時，{X1}與{X2}的相關系數較大，{X}受相鄰位置狀態影響明顯；隨著狀態轉移間隔k增大，{X1}與{X2}的相關系數變小，{X}受相鄰位置狀態影響減弱。

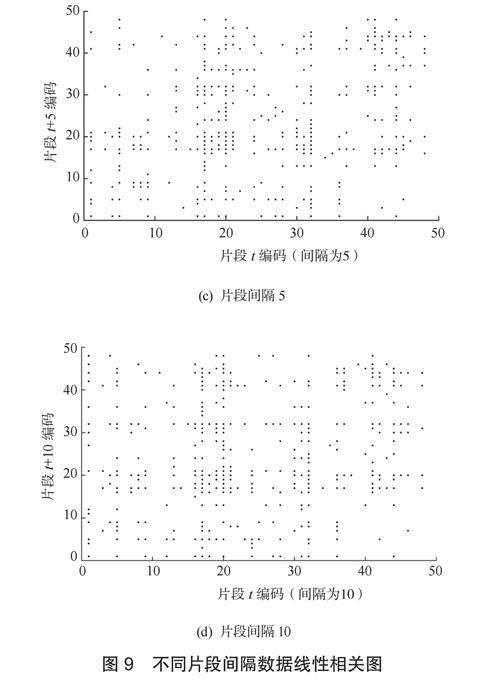
文中采用制動踏板位移、道路坡度和車速三參數構建時間連續Markov過程工況片段，分別選取片段間隔為1、2、5、10構造新狀態序列{X1}和{X2}，片段如圖9，不同片段間隔數據線性相關系數如表4。

為了定性分析不同片段間隔對{X1}與{X2}相關性的影響，采用Pearson相關系數進行評價，如式（7）。

不同片段間隔下新狀態序列的相關系數，如表4，當狀態轉移間隔k較小時，{X1}與{X2}的相關系數較大，說明當前片段狀態受相鄰位置處的狀態影響明顯；隨著狀態轉移間隔k增大，{X1}與{X2}的相關系數變小，說明當前片段狀態受相鄰位置處的狀態影響減弱，因此具有“Markov性”，其Markov過程合理。

2.2典型工況選取

為了解決Markov-MonteCarlo方法構建的工況的差異性，本文通過多次構建不同候選工況，從中選出與總體數據差異最小的工況構建典型工況。如表5所示，針對制動踏板位移、坡度、速度3個參數，共選取了22個具有統計意義的特征參數作為工況評估指標，工況評估指標之間的權重相同。

由式（8）與式（9），根據候選工況與總體數據各項特征參數的偏差δ及其均值確定工況，以偏差均值最小的工況構建典型工況。

其中，θi為候選工況第i類特征參數，θ為總體數據特征參數，δi為第i類特征參數偏差，δ?為候選工況偏差均值。

依據上述方法構建的典型工況，如圖10。為使數據可視化，將道路坡度信息與速度和制動踏板位移同步轉化為海拔高度隨行駛時間的變化序列，如圖11。獲得典型工況數據與總體數據特征參數對比如表6。

經對比分析，文中構建的典型工況數據與總體數據的偏差均值為5.66%，其時長為1238s，制動踏板平均位移為5.93mm，工作時長1194s，平均車速為65.34km/h，運行里程為21.18km，高差為757.10m，符合重型載貨汽車長下坡制動運行的特征。重型載貨汽車長下坡制動工況制動踏板位移范圍0～15mm，坡度范圍為0～6%，速度范圍為55～80km/h。

3制動工況辨識

3.1制動工況標準數據庫建立

標準數據庫采用K聚類方法建立，依據工況特征參數建立聚類分析與反向傳播（backpropagation，BP）神經網絡模型。考慮到制動工況特征參數較多，聚類邊界不明顯，為此通過特征參數之間的Pearson相關系數選取特征參數，如式（7）所示，部分結果如表7。

通常，Pearson相關系數0.8以上，兩者間有極強的相關性；0.6～0.8，有強相關性；0.4以下，有弱相關性或者沒有相關性。據此，選擇平均制動踏板動作位移Dom、最大制動踏板位移Dmax、平均制動踏板踩踏變化率Gsm、平均制動踏板位移松放變化率Glm4個特征參數，用于聚類分析與建立工況識別模型。

設置聚類狀態數K為3，聚類結果如圖12，橫坐標為平均制動踏板動作位移Dom，即短行程內制動踏板動作狀態下的位移平均值，縱坐標為短行程內最大速度與短行程末速度的差值Δv2，反映一個制動踏板動作短行程（一次制動行為）的制動效果。聚類結果分為3類，即弱制動工況，一般制動工況，強制動工況，每類工況各參數統計值見表8。

由表8，工況1制動踏板位移平均值與制動踏板位移最大值均處于較低水平，制動強度較弱，其短行程初速度與末速度差值為負值，呈現加速狀態；工況3制動踏板位移平均值與制動踏板位移最大值均處于較高水平，制動強度較強，其短行程初速度與末速度差值為正值，呈現減速狀態；工況2制動踏板工作位移平均值與制動踏板位移最大值均處于工況1與工況3之間，制動強度處于一般水平，短行程初速度與末速度差值接近于零，整體呈現勻速狀態。

綜上所述，定義以上工況為加速弱制動工況，其特征如工況1所述；勻速一般制動工況，其特征如工況2所述；減速強制動工況，其特征如工況3所述。為簡化工況特征，忽略坡度特性。

3.2工況模型訓練

BP神經網絡屬于多層前向網絡，具有復雜非線性映射、自學習能力，可用于求解內部機制復雜的問題，且不會隨數據量增大增加計算量，為此利用BP網絡建立制動工況識別模型。基本結構如圖13，由輸入層、隱含網絡層與輸出層組成，不同層之間通過具有一定權值與閾值的神經元連接。前向傳播由輸入層至輸出層逐層處理；如不能得到期望輸出，通過誤差逆向反饋，并以此對權值和閾值進行更新，迭代使輸出與期望值之間的誤差越來越小，以此訓練神經網絡模型。

設置學習效率η為0.0015，目標誤差為0.01，最多訓練次數為200萬次，中間神經元的數量為12，進行神經網絡訓練。針對本文數據塊數量特點，采用訓練集與測試集7：3將工況塊分類，即70%的樣本作為訓練集，工況1、工況2、工況3數量分別為4組、62組、191組；30%樣本作為測試集，工況1、工況2、工況3數量分別為4組、28組、83組。

3.3工況辨識與在線驗證

為了驗證構建工況的準確性，選取訓練集和驗證集數據進辨識驗證，測試集和驗證集神經網絡識別率達到100%，可以用于構建工況的識別，驗證結果如圖14和圖15。

為了保證在線識別的時效性，采用滾動時間窗識別策略，根據時間窗寬度內制動踏板動作數據，識別當前制動工況，以一定時間步長向前滾動采集制動踏板動作數據，實現對制動工況的持續識別。依據短行程片段進行定步長辨識，如圖16。

為提高識別精度，選擇合理時間步長，分別選取10、20……120s時間窗寬度以確定最優步長，比較結果如圖17，時間窗寬度60s時識別準確性最高，為此文中選取識別步長為60s。

以60s為步長對工況塊化處理，將其輸入至神經網絡，其識別結果如圖18所示。

依據表9對構建工況序列進行工況狀態賦予，如表9，驗證狀態如圖19所示。

構建工況識別與狀態賦予結果對比如圖20。定步長工況塊識別一般制動工況和強制動工況正確率為89.30%。

4結論

文中以山區公路行駛試驗數據為基礎，利用短行程劃分、K聚類和編碼技術建立了重型載貨汽車長下坡行駛工況，并對辨識方法展開研究。

以車輛行駛速度、制動踏板位移和道路坡度等特征參數對短行程數據進行統計分析，得到在山區公路行駛車輛的典型運動學片段，分析了片段間的Markov特性并利用Markov-MonteCarlo模擬方法彌補了Markov先驗不足的缺點，依據具有統計意義的特征參數對候選工況進行評估，最終得到重型載貨汽車長下坡制動工況，工況總時長1194s，長度21.18km。

以一定時間步長向前滾動實現對制動工況的持續識別，時間窗寬度60s時識別準確性最高；為了驗證重型載貨汽車長下坡制動工況識別模型的準確性，依據工況特征在線辨識，結果顯示一般制動工況和強制動工況正確率為89.30%，研究表明建立的工況識別模型可有效對制動工況進行識別。

下一步開展典型工況與特征參數權重的映射關系及基于長下坡制動工況辨識的制動控制策略研究。