聚集常態(tài)課堂 發(fā)展數(shù)學(xué)思維

黃雯

［摘 ?要］ 在新課程標(biāo)準(zhǔn)背景下，小學(xué)生數(shù)學(xué)核心素養(yǎng)的培養(yǎng)已經(jīng)成為當(dāng)前數(shù)學(xué)學(xué)科教學(xué)的根本方向，而學(xué)生思維能力的培養(yǎng)則是發(fā)展學(xué)生數(shù)學(xué)核心素養(yǎng)的重中之重。教師多樣化的教學(xué)模式、合理的教學(xué)設(shè)計(jì)就是幫助學(xué)生在數(shù)學(xué)課堂中發(fā)展數(shù)學(xué)思維能力的有效方式之一。文章以“三角形面積計(jì)算公式的推導(dǎo)”為例，立足課堂設(shè)計(jì)細(xì)節(jié)，淺談提升學(xué)生課堂思維能力的策略。

［關(guān)鍵詞］ 思維能力；教學(xué)設(shè)計(jì)；三角形的面積

一、數(shù)學(xué)思維的表現(xiàn)及培養(yǎng)現(xiàn)狀

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022年版）》中指出：在義務(wù)教育階段，數(shù)學(xué)思維的主要表現(xiàn)為運(yùn)算能力、推理意識(shí)或推理能力。通過(guò)數(shù)學(xué)思維可幫助學(xué)生掌握概念本質(zhì)、構(gòu)建知識(shí)結(jié)構(gòu)、推理相關(guān)結(jié)論、建立問(wèn)題模型等，幫助學(xué)生在學(xué)習(xí)數(shù)學(xué)知識(shí)的過(guò)程中凝練思考方法、提升個(gè)人能力。自全國(guó)各地大力實(shí)施課程改革以來(lái)，大部分一線教師更注重把課堂交還給學(xué)生，然而新時(shí)代背景下學(xué)生的學(xué)情是在不斷發(fā)展變化的，如何更加高效地從“教師陣地”轉(zhuǎn)變到“學(xué)生陣地”，在一節(jié)數(shù)學(xué)課中令各個(gè)思維層次的學(xué)生都能有所收獲，充分經(jīng)歷知識(shí)形成的過(guò)程，需要教師腳踏實(shí)地地在實(shí)踐教學(xué)中不斷摸索前進(jìn)，讓每一節(jié)數(shù)學(xué)課都成為為學(xué)生的思維發(fā)展而量身打造的階梯。

二、培養(yǎng)學(xué)生數(shù)學(xué)思維的重要性

1. 激發(fā)學(xué)生的學(xué)習(xí)興趣

教育心理學(xué)家皮亞杰說(shuō)：“所有智力方面的工作都要依賴于興趣。”與此同時(shí)，筆者認(rèn)為有效的思維過(guò)程恰恰是激發(fā)學(xué)習(xí)興趣的催化劑。研究表明，完成既定目標(biāo)帶來(lái)的成就感會(huì)使大腦持續(xù)更長(zhǎng)時(shí)間的興奮，影響力也更大。在研究數(shù)學(xué)知識(shí)時(shí)學(xué)生不僅需要調(diào)動(dòng)已有的知識(shí)學(xué)習(xí)經(jīng)驗(yàn)，還需要在此基礎(chǔ)上進(jìn)行“再創(chuàng)造”，完成知識(shí)和方法的二次延伸，進(jìn)而解決新的問(wèn)題。學(xué)生在這樣有效的思維過(guò)程中厘清知識(shí)脈絡(luò)，表達(dá)方法過(guò)程，建立數(shù)學(xué)模型，獲得解決新問(wèn)題、掌握新方法的成就感，會(huì)反過(guò)來(lái)激發(fā)其對(duì)數(shù)學(xué)的學(xué)習(xí)熱情。

2. 積累學(xué)生的學(xué)習(xí)經(jīng)驗(yàn)

現(xiàn)代課程改革的理念是以學(xué)生的發(fā)展為本，因此除了強(qiáng)調(diào)基礎(chǔ)知識(shí)和基本技能，還希望學(xué)生能夠感悟數(shù)學(xué)的基本思想，逐漸積累數(shù)學(xué)活動(dòng)，特別是思維活動(dòng)的經(jīng)驗(yàn)［１］。特定的數(shù)學(xué)知識(shí)在各個(gè)學(xué)段中并不是獨(dú)立存在的一個(gè)點(diǎn)，而是存在于完整的知識(shí)結(jié)構(gòu)體中，學(xué)生在一節(jié)數(shù)學(xué)課堂上參與的思維活動(dòng)，能夠幫助其積累學(xué)習(xí)活動(dòng)的經(jīng)驗(yàn)，提煉獲取知識(shí)的方法，在接下來(lái)的知識(shí)學(xué)習(xí)中舉一反三。學(xué)生積累的學(xué)習(xí)經(jīng)驗(yàn)，對(duì)其數(shù)學(xué)學(xué)習(xí)有著深遠(yuǎn)影響。除此之外，學(xué)生在思維發(fā)展過(guò)程中所積累的運(yùn)算、推理等數(shù)學(xué)能力，養(yǎng)成的合乎邏輯的數(shù)學(xué)思維品質(zhì)，也將在其他學(xué)科中發(fā)揮重要作用，推動(dòng)其全面發(fā)展。

3. 發(fā)展學(xué)生的核心素養(yǎng)

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022年版）》中將數(shù)學(xué)核心素養(yǎng)由10個(gè)增加為11個(gè)，各大素養(yǎng)分別對(duì)應(yīng)數(shù)學(xué)眼光、數(shù)學(xué)思維、數(shù)學(xué)語(yǔ)言。其中的“運(yùn)算能力”和“推理意識(shí)”兩大素養(yǎng)正是學(xué)生會(huì)用數(shù)學(xué)的思維思考現(xiàn)實(shí)世界的發(fā)展重點(diǎn)。理解算理、掌握算法，選擇合理、準(zhǔn)確的運(yùn)算策略解決問(wèn)題，從已有的事例出發(fā)尋找事物間的內(nèi)在規(guī)律，運(yùn)用類比、歸納的方法進(jìn)行合情推理以使學(xué)生能分析、解決現(xiàn)實(shí)中的數(shù)學(xué)問(wèn)題，都是在幫助學(xué)生形成有理有據(jù)、依理而行的理性精神。王憲昌教授曾在書中提到數(shù)學(xué)思維可以使人在處理問(wèn)題時(shí)迅速抓住事物的本質(zhì)，從而找到解決問(wèn)題的辦法，還可以使人們形成良好的思維習(xí)慣，增加人們?cè)谔幚韱?wèn)題時(shí)的能力［２］。數(shù)學(xué)思維的培養(yǎng)幫助學(xué)生獲得適應(yīng)未來(lái)生活和進(jìn)一步發(fā)展所必須的關(guān)鍵能力，體現(xiàn)數(shù)學(xué)課程的育人價(jià)值，是發(fā)展學(xué)生核心素養(yǎng)的最終目標(biāo)。

三、課堂中培養(yǎng)學(xué)生數(shù)學(xué)思維的策略

以上，無(wú)論是從國(guó)家在數(shù)學(xué)教育導(dǎo)向的大格局出發(fā)，還是從學(xué)生終身學(xué)習(xí)的角度考慮，對(duì)學(xué)生數(shù)學(xué)思維的培養(yǎng)都應(yīng)該是教書育人的重中之重。

培養(yǎng)學(xué)生的數(shù)學(xué)思維，不僅需要教師在課堂實(shí)踐中有豐富的教學(xué)經(jīng)驗(yàn)，面對(duì)學(xué)生的課堂生成隨機(jī)應(yīng)變，還需要教師在掌握學(xué)情、精讀教材后進(jìn)行更加貼合學(xué)生思維基礎(chǔ)、更加順應(yīng)學(xué)生思維發(fā)展的教學(xué)設(shè)計(jì)。唯有雙管齊下，教師才能做好課堂中的“掌舵人”。本文以人教版五年級(jí)上冊(cè)“三角形的面積”的教學(xué)設(shè)計(jì)為例談?wù)勅绾闻囵B(yǎng)學(xué)生的推理意識(shí)和運(yùn)算能力，發(fā)展學(xué)生的數(shù)學(xué)思維。具體策略如下：

1. 精析關(guān)鍵問(wèn)題，指明思維方向

奧蘇貝爾的有意義學(xué)習(xí)理論中提到，發(fā)生有意義的學(xué)習(xí)的三大主觀條件之一是學(xué)習(xí)者的認(rèn)知結(jié)構(gòu)中必須具有能夠同化新知識(shí)的適當(dāng)?shù)恼J(rèn)知結(jié)構(gòu)。而在正式學(xué)習(xí)三角形面積之前，學(xué)生已經(jīng)充分掌握了平行四邊形面積的推導(dǎo)過(guò)程，明晰平行四邊形面積與底邊和此底邊對(duì)應(yīng)的高有關(guān)，這是所有學(xué)生學(xué)習(xí)這節(jié)課的知識(shí)方法基礎(chǔ)。除此之外，根據(jù)學(xué)情將學(xué)生大致分為三類：

（1）掌握三角形的面積計(jì)算公式但不清楚推導(dǎo)過(guò)程的學(xué)生；

（2）了解到三角形面積與其底和高有關(guān)但不清楚具體關(guān)系的學(xué)生；

（3）對(duì)三角形面積完全沒(méi)有前期思考的學(xué)生。

根據(jù)所呈現(xiàn)的三種不同的認(rèn)知結(jié)構(gòu)基礎(chǔ)的學(xué)情，為保證學(xué)生在實(shí)踐之前有充分的思考，用思維成果指引實(shí)踐操作，筆者設(shè)計(jì)了如下問(wèn)題：

（1）三角形面積的大小和什么有關(guān)？

（2）三角形面積大小是否與底和高有關(guān)？（幾何畫板實(shí)時(shí)拖動(dòng)演示，學(xué)生直觀感受并驗(yàn)證）

（3）三角形面積與底和高究竟有怎樣的關(guān)系？

（4）如何開(kāi)展對(duì)三角形面積計(jì)算公式的探索？

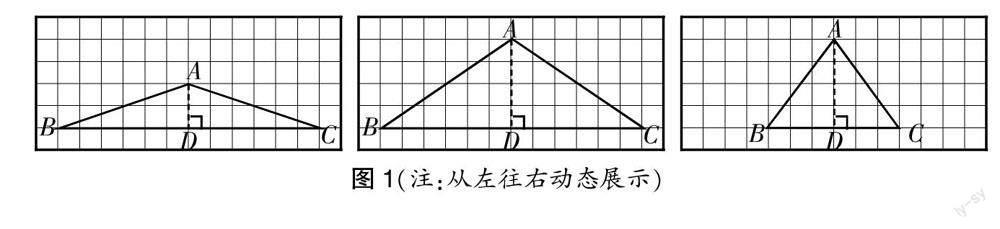
四個(gè)問(wèn)題環(huán)環(huán)相扣，教師完全尊重各類學(xué)情的學(xué)生在舊知和生活中對(duì)三角形面積計(jì)算的已有基礎(chǔ)，先詢問(wèn)學(xué)生影響三角形面積大小的關(guān)鍵因素，由此引發(fā)三類學(xué)生的思考；再借助先進(jìn)信息技術(shù)手段直觀演示三角形的高不斷拉長(zhǎng)或底不斷縮短對(duì)三角形面積造成的影響（如圖1），驗(yàn)證第2類和第3類學(xué)生猜想的同時(shí)，引導(dǎo)所有學(xué)生將思維聚焦在三角形的底和高上；最后激發(fā)所有學(xué)生思考探索三角形面積的方法，與已掌握的平行四邊形面積的研究方法接軌，從簡(jiǎn)單的知識(shí)關(guān)聯(lián)學(xué)習(xí)中重點(diǎn)提煉數(shù)學(xué)思想方法——“轉(zhuǎn)化”。分層設(shè)計(jì)的問(wèn)題為不同學(xué)情的學(xué)生保留了可貴的思考空間，讓不同思維水平的學(xué)生在對(duì)三角形面積的觀察、比較、思考中都能得到發(fā)展。

2. 精準(zhǔn)學(xué)材設(shè)計(jì)，把握思維梯度

多樣化學(xué)具的設(shè)計(jì)供擁有不同原始經(jīng)驗(yàn)的學(xué)生選擇，為不同層次的學(xué)生搭建思維階梯。人教版教材中，三角形面積的推導(dǎo)主要是通過(guò)將兩個(gè)完全一樣的三角形倍拼成平行四邊形來(lái)完成的。課堂上教師直接提供兩個(gè)完全一樣的三角形學(xué)具暗示過(guò)于明顯，也過(guò)于簡(jiǎn)單，大大局限了學(xué)生的思維。但如果直接棄而不用，難度較高的割補(bǔ)法也會(huì)使一部分學(xué)生無(wú)法“消化”。于是，為各個(gè)思維層次學(xué)生考慮，為推導(dǎo)三角形面積方法多樣化搭橋鋪路，筆者分別給不同小組準(zhǔn)備了以下幾類學(xué)具：

（2個(gè)全等直角三角形和1個(gè)普通銳角三角形）

（2個(gè)全等銳角三角形和1個(gè)直角三角形）

（2個(gè)全等鈍角三角形和1個(gè)銳角三角形）

（1個(gè)大等腰三角形和1個(gè)小等腰三角形）

每組學(xué)生均配備了一把安全剪刀。

每個(gè)小組的學(xué)具各有不同，如何選擇學(xué)具進(jìn)而確定研究方法需要小組成員共同開(kāi)動(dòng)腦筋，旨在啟發(fā)學(xué)生對(duì)手中的學(xué)具進(jìn)行觀察、比較、嘗試。在這個(gè)過(guò)程中思維難度較小的倍拼法和思維難度較大的割補(bǔ)法均有可能出現(xiàn)。而為了打破學(xué)生或許存在的“倍拼法”的固化思維，筆者特意設(shè)計(jì)第4組大小不一的兩個(gè)等腰三角形。在研究過(guò)程中學(xué)生既可以把大三角形剪成小三角形用倍拼法完成，又可以利用其中一個(gè)等腰三角形進(jìn)行較簡(jiǎn)單的沿底邊的高剪開(kāi)的割補(bǔ)法。

這樣的學(xué)材設(shè)計(jì)既貼近學(xué)生的學(xué)情，又給予學(xué)生充分的自主探索機(jī)會(huì)。教師徹底放手，通過(guò)學(xué)生自己生成的思維成果主導(dǎo)課堂、推動(dòng)課堂。

3. 精設(shè)匯報(bào)過(guò)程，引領(lǐng)思維碰撞

學(xué)生展開(kāi)互動(dòng)交流，并相互點(diǎn)撥與相互幫助，進(jìn)而建構(gòu)系統(tǒng)的知識(shí)網(wǎng)絡(luò)，逐步發(fā)展思維的系統(tǒng)性。本節(jié)課中，筆者精心設(shè)計(jì)匯報(bào)過(guò)程，層層推進(jìn)，將思維碰撞出的火花聚焦成關(guān)鍵問(wèn)題，引領(lǐng)學(xué)生進(jìn)行一場(chǎng)“燒腦”大作戰(zhàn)。

在匯報(bào)方式上，由學(xué)生主動(dòng)匯報(bào)本小組研究的三角形類型及研究方法和結(jié)果，包括對(duì)三角形的具體操作（剪或拼）和對(duì)三角形面積計(jì)算公式的推導(dǎo)。在匯報(bào)過(guò)程中，有疑問(wèn)的學(xué)生可以提出問(wèn)題，由匯報(bào)小組成員解答。

在匯報(bào)順序上，由于倍拼法較為簡(jiǎn)單，貼合大部分學(xué)生的思維水平，筆者有意將不同類型三角形倍拼法的推導(dǎo)過(guò)程安排在匯報(bào)前期。這樣一方面能調(diào)動(dòng)大部分學(xué)生思考不同類型三角形在進(jìn)行倍拼法時(shí)的相同之處，加深理解倍拼法必須滿足“兩個(gè)完全一樣的三角形”的基礎(chǔ)條件，另一方面通過(guò)三種類型三角形面積的研究，能引導(dǎo)學(xué)生總結(jié)一般三角形的面積計(jì)算公式。讓思維難度更大的割補(bǔ)法匯報(bào)緊隨其后，在原有倍拼法的基礎(chǔ)上給學(xué)生呈現(xiàn)完全不同的推導(dǎo)方法，這樣的思維碰撞極大地激發(fā)了學(xué)生的數(shù)學(xué)興趣，進(jìn)一步打開(kāi)了學(xué)生的數(shù)學(xué)視野，很好地體現(xiàn)了數(shù)學(xué)的魅力。

在匯報(bào)結(jié)果上，筆者聚焦兩種不同推導(dǎo)方法所得出的相同公式的含義，引發(fā)學(xué)生展開(kāi)討論，根據(jù)推導(dǎo)過(guò)程判斷相同公式中的“÷2”的含義是否一樣，說(shuō)明理由。筆者讓學(xué)生在回顧牢記公式中的“÷2”的同時(shí)，通過(guò)比較思維明白知其然并知其所以然的重要性。

筆者合理設(shè)計(jì)匯報(bào)過(guò)程，關(guān)注匯報(bào)細(xì)節(jié)，讓學(xué)生進(jìn)行思維交流，細(xì)細(xì)聆聽(tīng)每一個(gè)聲音，抓住最有價(jià)值的思考內(nèi)容，能促進(jìn)全班學(xué)生高效思考，使課堂教學(xué)達(dá)到高潮。

4. 精選分層練習(xí)，完成思維拔節(jié)

練習(xí)是鞏固應(yīng)用的主要形式，精心設(shè)計(jì)能拓展學(xué)生思維的廣度，讓學(xué)生從多角度、全方位對(duì)這個(gè)問(wèn)題進(jìn)行思考，在練習(xí)過(guò)程中發(fā)現(xiàn)數(shù)學(xué)的獨(dú)特魅力，具備更強(qiáng)的邏輯思維能力［３］。不同層次練習(xí)題的訓(xùn)練目的有所不同，基礎(chǔ)類練習(xí)題幫助所有學(xué)生夯實(shí)本節(jié)課的基礎(chǔ)知識(shí)，在實(shí)際應(yīng)用中將三角形面積的求解公式內(nèi)化于心。拓展類練習(xí)題既可以幫助思維水平一般的學(xué)生開(kāi)闊視野，又可以幫助學(xué)有余力的學(xué)生進(jìn)一步研究。基礎(chǔ)類練習(xí)題必不可少，拓展類練習(xí)題也是重中之重，是一節(jié)課的思維之光。筆者在“三角形的面積”一課中設(shè)計(jì)了如下拓展類練習(xí)題（如圖2）供學(xué)生研究思考：

問(wèn)題1：觀察圖形，你發(fā)現(xiàn)了什么？

問(wèn)題2：在方格紙最右邊畫出和三角形①面積相等的三角形，你能畫出多少個(gè)？

問(wèn)題1旨在引導(dǎo)學(xué)生先獨(dú)立思考后與同桌討論，從三角形①②③中得出“等底等高三角形的面積相等”的結(jié)論；再結(jié)合三角形④⑤進(jìn)而得出面積相等的三角形的底和高不一定相等，但是底和高的乘積一定相等，進(jìn)而讓學(xué)生感受數(shù)學(xué)中的“變與不變”，感受千變?nèi)f化的數(shù)學(xué)。

問(wèn)題2旨在引導(dǎo)學(xué)生運(yùn)用等底等高的三角形面積相等這一結(jié)論動(dòng)手操作，與四年級(jí)上冊(cè)內(nèi)容“平行與垂直”知識(shí)相結(jié)合，進(jìn)而發(fā)現(xiàn)這樣的三角形可以畫無(wú)數(shù)個(gè)。

這樣的拓展類練習(xí)題使得學(xué)生的思維水平邁上一個(gè)新的臺(tái)階，教會(huì)學(xué)生從基礎(chǔ)簡(jiǎn)單的知識(shí)中找到新舊知識(shí)之間的聯(lián)系，讓不同思維層次的學(xué)生都獲得訓(xùn)練，完成思維拔節(jié)。

思維能力的發(fā)展是終身的，在任何階段教育工作者都應(yīng)該善于發(fā)掘?qū)W生的思維潛力，善于評(píng)估學(xué)生的思維水平，也應(yīng)該竭力為學(xué)生的思維能力的發(fā)展做出努力。課堂教學(xué)是一線教師在日常教學(xué)中接觸最多的內(nèi)容，恰恰由于日常，反而容易被忽視其重要的價(jià)值。然而，平凡的堅(jiān)守往往能取得豐碩的成果。如果一線教師能夠在日常教學(xué)中加入對(duì)學(xué)生數(shù)學(xué)思維能力培養(yǎng)的思考，在每節(jié)課的教學(xué)設(shè)計(jì)和教學(xué)實(shí)踐中有所體現(xiàn)，那么每節(jié)數(shù)學(xué)課內(nèi)含的思維的廣度和深度會(huì)潛移默化地使學(xué)生的數(shù)學(xué)眼光、數(shù)學(xué)思維和數(shù)學(xué)語(yǔ)言更上一個(gè)層次。

參考文獻(xiàn)：

［１］ 史寧中.基本概念與運(yùn)算法則——小學(xué)數(shù)學(xué)教學(xué)中的核心問(wèn)題［Ｍ］. 北京：高等教育出版社，２０１３.

［２］ 王憲昌. 數(shù)學(xué)思維方法［Ｍ］. 北京：人民教育出版社，２０１０.

［３］ 張敏. 如何培養(yǎng)小學(xué)生的數(shù)學(xué)思維能力［Ｊ］. 數(shù)學(xué)學(xué)習(xí)與研究，２０１６（０４）：８０.