借助矩形模型圖式探尋乘法運算的一致性
王燕珠
矩形模型圖式有助于計數單位的認識,有助于貫連小學階段的整數乘法、小數乘法和分數乘法。基于數的認識和數的運算的一致性,筆者通過整數、小數和分數的計數單位的整體認識,幫助學生形成和發展數感,并借助矩形模型圖式探尋乘法運算的一致性,以加深學生對數學學習的整體感悟和一致性感知,發現數學的至簡之美。
一、問題的提出
在一節小學數學分數乘分數的課堂教學里,面對“用面積模型表示3/4的1/4是多少”這個學習任務,一個學生突然很沮喪:“不是3/4的1/4嗎?我也是把3/4再平均分成4份,可是這樣畫看不出結果是多少?”細看他畫的圖,原來他嘗試把3/4的部分再次豎著平均分成了4份,兩次均分都是豎著分,為什么不能直觀看出結果呢?學生為什么堅持豎著兩次均分呢?
是的,“3/4的部分再次豎著平均分成了4份”并不能直觀看出原單位面積圖形到底被平均分成了幾份,可以把3/4看成300/400,300份就能被均分成4份了。學生堅持豎著兩次均分主要是因為受習慣影響,在前面分數乘法的學習中,碰到的基本是單次均分,要么單次豎著均分,要么單次橫著均分,都可直觀看出結果。那么如何引導學生進一步認可“求3/4的1/4是多少,用乘法計算”?如何引導學生理解需要橫向和縱向二維觀察的面積模型表示分數乘法?
對于面積模型學生并不陌生,縱觀北師大版小學數學教材,在整數乘法、小數乘法、分數乘法都有不少的涉及和使用,其他版本教材也基本如此。用面積模型表示分數乘分數時,需要橫向和縱向的二維觀察,按理說學生是不陌生的。那么問題在哪里呢?問題就出在“為什么要用面積模型?”顯然不是“因為面積模型一目了然,很直觀”就可以回答清楚的,必須弄明白面積模型使用的必要性。實際上,乘法運算本身,在計算3/4×1/4=3/16時產生了新的分數單位1/16,可借助面積模型直觀得到。關于分數乘法里的面積模型,研究者劉加霞將其列為乘法的現實模型之一,稱之為矩形模型。這里的矩形模型在整數乘法里實際上就是點陣圖,在小數乘法和分數乘法里就是面積模型,所以基于對整數、小數、分數乘法運算的整體性理解,筆者將其稱之為矩形模型,對應的圖式就是矩形模型圖式。另外,要充分認識數的運算的一致性,要清楚“數的認識的一致性”這個前提,基于數的認識和數的運算的一致性,筆者通過整數、小數和分數的計數單位的整體認識,幫助學生形成和發展數感,并借助矩形模型圖式探尋乘法運算的一致性,以加深學生對數學學習的整體感悟和一致性感知,發現數學的至簡之美。
二、借助矩形模型圖示,探尋乘法運算的一致性
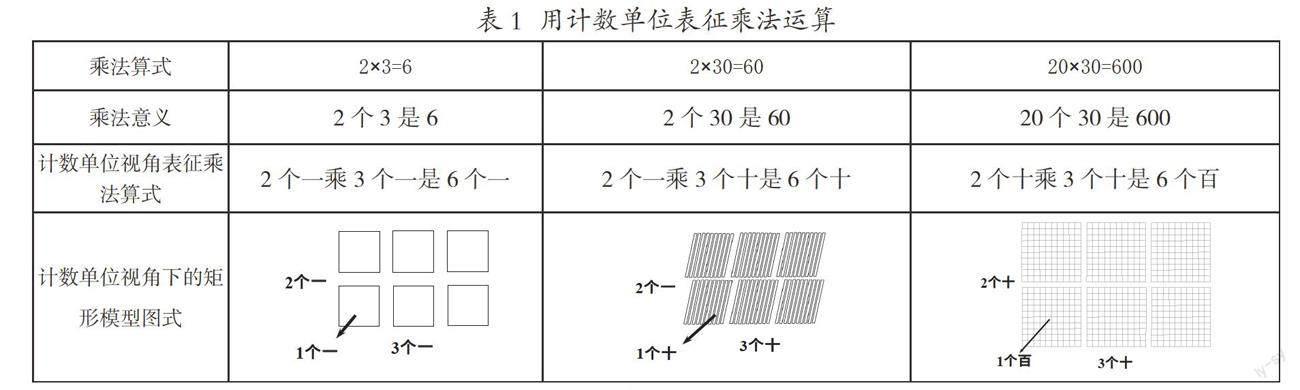
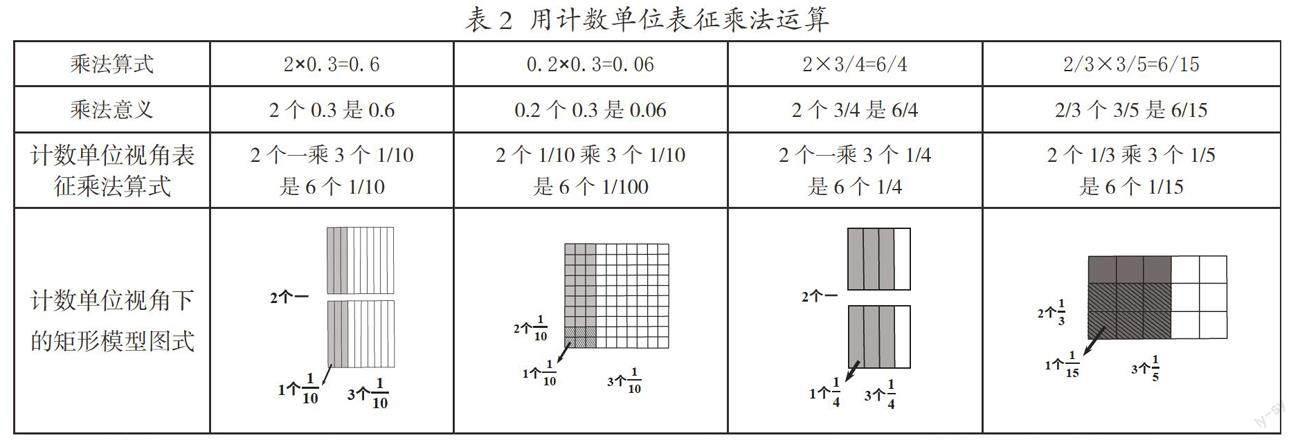
相比乘法現實意義的多樣性,乘法算理更具一般性,算理承載著數和數運算的抽象發展,肩負著學生數感的形成,承擔著促使學生運算能力提升的關鍵作用,所以,算理的探索是小學學習最重要的任務之一。如果能將乘法算理和乘法現實意義相聯系,學生的發現問題、提出問題、分析問題和解決問題的能力也會隨之發展和提升。基于乘法的現實意義,研究者劉加霞將乘法的現實模型概括為等量組的聚集模型、倍數模型、配對模型和矩形模型,并進一步指出最基本的是聚集模型,其他幾種模型都可以轉化為聚集模型。這里由于要借助矩形模型圖來認識計數單位視角下的乘法運算,筆者嘗試用等量組的聚集模型這個最基本的模型來認識乘法的意義,以溝通乘法算理與乘法意義之間的聯系,進一步認識乘法運算的一致性,如表1、表2所示(用計數單位表征乘法運算)。
(一)整數乘法運算的一致性
以2×3=6、2×30=60、20×30=600這三種情形為例,用“往回看”的方法,先看整十乘整十的情況,最為熟知的一條規律就是“先不看乘數末尾的0,2和3相乘得6,乘數末尾共有幾個0,就在6的后面添上幾個0”,如果這樣的規律發現僅通過幾組乘法算式得到,而沒有加以解釋,那么就喪失了很多說理明理的數學學習機會。2個十乘3個十,得到了與20、30這兩個乘數都不一樣的計數單位“百”,乘法運算過程里誕生了新的計數單位,借助矩形模型的圖式可以清楚地看到:橫向觀察是3個十,豎向觀察是2個十,根據行列的排列規則,先看10行10列,十個十就是百,先有一個百,再依據排列(2排3列)的順序,共能數出6個百。以此類推,借助千的立方體觀察20×300,可以觀察到10個100得1個千,共得到6個千,所以20×300=6000。
用同樣的方法繼續“往回看”2×30=60和2×3=6,根據排列順序,分別共得6個十和6個一,也就是60和6。從自然數的角度看數感的形成和發展,有研究表明,人們普遍天生有個數方面的數感,容易察覺到幾個一,而對于幾十個幾十,幾十個幾百等不是“一”的計數單位,就難以對結果有明確感知。行列的有序排列,也就是矩形模型圖式,貫通了乘法和加法的聯系,使人們可以在乘法的運算中,感受到數的不斷累積,進一步形成和發展與較大計數單位有關的數感。
(二)小數乘法運算的一致性
以2×0.3=0.6、0.2×0.3=0.06為例來看小數乘法,2個0.3實際上就是2個3/10,觀察矩形模型圖式,橫向看是2個一,豎向看是3個1/10,1個一先乘1個1/10得1個1/10,計數單位與乘數0.3的一樣,再根據行列順序數一數,共得6個1/10。算式0.2×0.3=0.06,2個0.1和3個0.1相乘為什么得到兩位小數0.06呢?得數的計數單位與乘數0.2和0.3為什么都不一樣呢?觀察矩形模型圖式,可以將0.2×0.3理解為0.2個0.3,即2/10個3/10,那么就要先關注1/10個1/10,也就是1/10的1/10,為1/100,1/10個1/10是1個1/100,得到了新的計數單位1/100,根據行列排列的順序數一數可得6個1/100,為6個0.01,是0.06。
小數是基于現實生活度量的需要,由于度量需求的精準,需要十等分、再十等分、繼續十等分等,它是一種更具現實意義的數。但是小數乘法算理仍是建立在分數乘法算理的基礎上,且基本與分數乘法算理一致,由于小數是更具現實意義的一種數,要形成和發展關于小數的數感,必須通過分數的意義和分數乘法的算理來深刻認識小數和小數乘法最原本的模樣,再結合小數豐富的現實意義,進一步發展與小數有關的數感和量感,完成對小數這一具有明顯現實意義模型的進階認識。
(三)分數乘法運算的一致性
分數的乘法運算是建立在分數的意義、分數單位、真分數和假分數等知識的基礎上的,通過分數乘法運算進一步認識分數的意義,認識到分數與整數、小數一樣都有明確的計數單位,分數的計數單位就是分數的分數單位,分數的乘法運算同整數乘法和小數乘法一樣,是基于計數單位的累加,在算理上是一致的。算式2×3/4=6/4,表示2個3/4是6/4,即2個一乘3個1/4是6個1/4,觀察矩形模型圖示,1個一和1個1/4相乘,得1個1/4,乘積的計數單位和3/4一樣,再根據行列的排列順序,共6個1/4,得6/4,化成最簡分數后是3/2。另外,根據分數的意義和倍數的知識儲備,將3/4理解為一個倍率,一個數的幾分之幾是多少相當于求一個數的幾倍是多少,都可以用乘法計算,對部分學生來說,這樣的類比推理是有現實意義的,也是可以抽象理解的。但考慮到小學生身心發展的特點,抽象意識還有待萌芽和發展,那么如何使學生認可“一個數的幾分之幾是多少,用乘法計算”這一基本事實呢?實際上,根據畫圖操作,學生不難發現2的3/4是6個1/4,即6/4,2個3/4也就是6個1/4,也得6/4,因此從計數單位的視角觀察操作過程和操作結果都能發現:2的3/4是多少,相當于求2個3/4是多少,再給學生提供多一些的具有現實意義的分數情境問題,在不斷的獨立思考、合作交流中進一步認識和發現其中的規律,促使學生不斷認可“一個數的幾分之幾是多少,用乘法計算”這一基本事實。
求2/3的3/5是多少為什么用乘法列式?學生難以具象化認識其中的關聯,借助矩形模型圖示可以解決這一問題。根據分數的意義,“2/3的3/5是多少”也可做矩形模型圖示,豎向看是2個1/3,橫向看是3個1/5,先用行列排序的方式觀察計數單位的情況,1/3個1/5就是1/15,用計數單位1/15來數一數,共有6個1/15,得6/15,化成最簡分數后是2/5。從行列的觀察角度還能進一步發現,矩形模型圖示表示的也是2/3個3/5,列式為2/3×3/5。只從一個數的幾分之幾是多少來觀察矩形模型圖示,這里仍存在一個疑惑點:為什么2/3的3/5是多少,得數的計數單位是兩個乘數的計數單位的乘積呢?學生如果只關注分數的意義,停留在不斷思考“2/3的3/5是多少”這個問題本身,不但想不明白結果是多少,也難以想明白2/3的3/5為什么也用乘法計算。一般來說,求2/3的3/5是多少,其結果仍是相當于求2/3的3/5的部分占原單位“1”的幾分之幾,所以如果把思考的焦點聚集在原單位“1”被均分的情況,很快就能活絡學習思路,用行列的觀察方法來看待分數乘法,就能明白2/3×3/5=6/15像2×3=6一樣,2個3是6,2個1/3乘3個1/5是6個1/15,即2/3個3/5是6個1/15,得6/15。
(四)乘法運算的一致性
上文分別根據整數、小數和分數的學習和對應的乘法運算學習脈絡,借助矩形模型圖示,用行列排序的觀察方法呈現了乘法運算的一致性。回看矩形模型圖示,可以進一步總結和發現乘法運算一致性主要體現在兩個方面:第一,乘積的計數單位就是兩個乘數的計數單位相乘。乘積的計數單位具體如何產生,要結合具體的圖示,主要有兩種情況,一是與其中一個乘數的計數單位一樣,這類一般是其中一個乘數的計數單位是一,那么乘積的計數單位就與另一個乘數的計數單位一樣;二是乘積的計數單位與兩個乘數的計數單位都不一樣,結合矩形模型圖示的觀察,順著行列排序的順序,先豎向看再橫向看,或者先橫向看再豎向看,如果觀察得到十個十,會產生新的計數單位百,如果觀察得到1/10個1/10,會產生新的計數單位1/100,以此類推。第二,無論是從乘法的意義出發,還是從乘法的算理出發,都能回歸到“幾個幾”來進一步探究,因為乘法是加法的簡便運算,乘積就是計數單位累加的結果。
三、結語
基于運算的整體性視角,乘法運算的一致性學習需要學生主動參與乘法運算算理探討的過程,觀察和明晰說理。教師要密切關注計數單位的學習,以計數單位的學習為抓手,重視矩形模型圖式的應用,多用數理的方式展開乘法算理的學習,讓學生能看到、能推理、能言說,提升學生對乘法運算的一致性認識和理解,助推學生數學核心素養的形成和發展。

