我國近20年數學解題研究熱點與發展趨勢

王澤學　陳維

摘 要：基于BICOMB2和SPSS26.0分析軟件，對來自CNKI的2015篇有關數學解題的有效文獻進行可視化分析，根據熱點知識圖譜了解我國近20年數學解題研究熱點和發展趨勢.我國數學解題的研究熱點由“解題策略以及解題教學”；“解題反思：一題多解”；“解題思路、技巧以及思想與方法”三個方面組成.研究熱點領域呈現出四大發展趨勢：解題中滲透數學思想方法，培養數學核心素養;不等式問題探究;波利亞中的元認知思想；注重解題教學中反思能力.

關鍵詞：數學解題；研究熱點；發展趨勢；知識圖譜

2021年國務院辦公廳印發《關于進一步減輕義務教育階段學生作業負擔和校外培訓負擔的意見》（以下簡稱《“雙減”政策》），指出“減輕學生過重作業負擔”［1］.那這是不是意味著數學習題對于數學的學習不再那么重要？曾經，在國際數學教育界就出現過“中國學習者悖論”，即中國學生的數學學習成績優良，但其創新和思維能力不足［2］.前者是我國熟能生巧理念，雙基的實施等等所帶來的，而后者就是過重的作業負擔，機械地做題所產生的.但對于數學而言，不做題肯定是行不通的.波利亞說：“掌握數學就是意味著善于解題［3］.”單壿教授在《解題研究》談到解題重要性說；“學數學的目的，不為別的，就是為了學會解題［4］.”這充分說明數學解題的重要性，那怎樣解題以及解題教學在《“雙減”政策》的背景下更至關重要，我國對于數學解題的研究成果也碩果累累.因此利用BICOMB2和SPSS26.0分析軟件對數學解題研究領域的文獻進行系統梳理，對我國近二十年數學解題研究現狀以及發展趨勢進行直觀呈現，便于數學解題領域的研究者們進行下一步的探究.

1 研究數據和方法

1.1 研究數據

以中國知網（CNKI）中的學術期刊與學位論文作為文獻來源，以“數學解題”為主題進行檢索，時間跨度為2003—2022年，時間截止至2022年11月28日.檢索到學術期刊論文1519篇，碩博士論文714篇，共2233篇，利用“檢索—初篩—納入—綜合”4個步驟進行甄選［5］，最終選定有效文獻2015篇.

1.2 研究方法

利用Bicomb2和SPSS26.0軟件進行分析.從高頻關鍵詞、近似值矩陣、聚類圖和熱點知識圖譜四個方面對數學解題研究領域進行解讀.這種方法不僅能直觀地揭示該領域的研究熱點以及熱點間的關系，還能對該領域發展趨勢進行預測.

2 研究過程

2.1 確定高頻關鍵詞

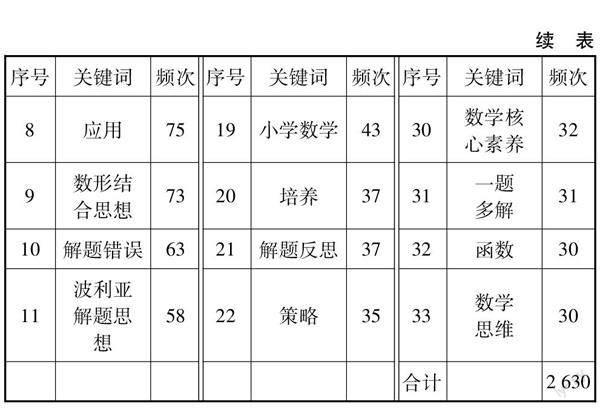
首先，利用Bicomb2分析軟件提取并統計關鍵詞，獲得2538關鍵詞；其次，將含義重合的關鍵詞進行合并，如將“解題”和“數學解題”合并為“數學解題”等，得到有效關鍵詞的頻次為6845次；最后，截取累計頻次為40%左右的關鍵詞為高頻關鍵詞，共獲得33個關鍵詞，結果見表1.

從表1可以看出，33個高頻關鍵詞的頻次之和為2630次，占總頻次的38.42%.其中排名前10的關鍵詞出現頻次均大于60，分別是數學解題（456），中學數學（322），解題教學（231），解題能力（178），中學生（120），數學思想方法（94），解題策略（90），應用（75），數形結合思想（73），解題錯誤（63）.可見我國數學解題領域的研究多以中學生解題能力、解題策略、解題錯誤、解題中思想方法以及中學數學解題教學為主.而波利亞解題思想（58）、構造法（55）出現的頻次也大于等于55，說明在解題策略和解題方法的研究中，波利亞解題思想和構造法最受關注.

2.2 生成近似值矩陣

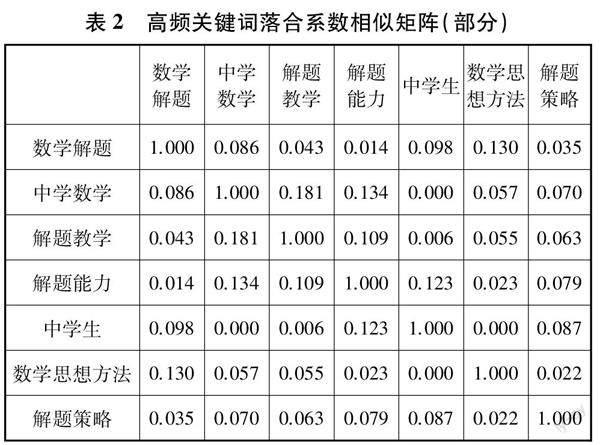
利用Bicomb2分析軟件對上述的33個高頻關鍵詞進行共詞分析，生成詞篇矩陣并導入SPSS26.0，選取落合系數得到相似矩陣，結果見表2.

表2中的數字反映了兩關鍵詞之間的相似度，數字越大，兩關鍵詞間距離越近，相似度越高，反之距離越遠，相似度越低.表2中，各個關鍵詞到“數學解題”距離由近及遠的順序依次為：數學思想方法（0.130）、中學生（0.098）、中學數學（0.086）、解題教學（0.043）、解題策略（0.035）、解題能力（0.014）.可見“數學解題”與“數學思想方法”“中學生”“中學數學”之間的距離最近，這說明研究者們在數學解題研究領域中，更關注中學階段以及解題中的數學思想方法.

2.3 生成高頻關鍵詞聚類圖

為了更直觀呈現高頻關鍵詞間的關系，利用SPSS26對BICOMB2軟件生成的詞篇矩陣進行聚類分析，如圖1所示.

圖1中，縱軸數字代表與之相應的高頻關鍵詞，橫軸數字代表關鍵詞之間的距離，數字越小，表明距離越近，關系更密切［6］.從數學解題高頻關鍵詞聚類圖（圖1）可直觀看出33高頻關鍵詞被分為3大類.種類1為“解題策略以及解題教學”研究，包括解題策略、數學應用題、小學數學、解題能力、培養、審題、解題教學等16個關鍵詞;種類2為“解題反思：一題多解”研究，包括解題反思、一題多解2個關鍵詞；種類3為“解題思路、技巧以及思想與方法”研究，包括解題技巧、不等式、中學數學、函數、解題思路、解題方法、數學思想方法等15個關鍵詞.

2.4 繪制數學解題研究熱點的可視化圖譜

用SPSS26進行多維尺度分析，并選擇Z分數進行標準化，結合聚類分析結果，繪制出數學解題研究熱點知識圖譜.結果見圖2.

從圖2可以看出，解題策略以及解題教學研究（領域1）位于第三、第四象限，其中在第三象限中，“解題策略”“解題錯誤”“波利亞解題思想”“解題教學”“培養”“數學核心素養”“數學應用題”關鍵詞在Y軸距離較近，這表明在解題策略中運用波利亞解題思想，數學應用題中避免解題錯誤以及在解題教學中培養數學核心素養研究已經形成了一定的研究規模，但并未處于整個研究網絡的中心.“元認知”“問題解決”“數學思維”“審題”“小學數學”等關鍵詞位于第四象限，是整個領域的邊緣主題，研究者們很少關注，因此在培養小學數學的數學思維，問題解決中的元認知思想，數學解題中的審題等方面也需要引起重視.

解題思路、技巧以及思想與方法的研究（領域3）位于第一、第二象限，在第一象限中，“中學數學”“函數”“解題方法”“解題技巧”“解題思路”各關鍵詞間聯系較為緊密，表明中學數學對函數、不等式的解題思路、技巧以及方法研究成果較為豐富，也是現階段此領域中的熱點、重點.在第二象限中，“數學解題”“數學思想方法”等關鍵詞聯系緊密，又形成數學解題中運用數學思想方法研究領域，同時與“解題反思：一題多解”研究（領域2）位于同一象限，表明這兩個領域的研究較為活躍，未來可以探究思考將這兩個領域的研究與其他領域關聯起來.

3 數學解題研究發展趨勢分析

3.1 解題中滲透數學思想方法，培養數學核心素養

在圖2中，領域3中“數學解題”“數學思想方法”等五個關鍵詞聯系較為緊密，形成在數學解題中滲透數學思想方法研究領域.經徐利治教授的倡導下，近幾十年，數學思想方法已經成為廣大教師頻繁使用的詞語，在數學解題教學中滲透數學思想方法已為廣大教師所接受.因此也引來了研究者們樂此不疲地進行探究.領域1中“解題教學”“培養”“數學核心素養”三個關鍵詞在Y軸距離較近，形成解題教學中培養數學核心素養研究領域.2014年教育部發布《關于全面深化課程改革落實立德樹人根本任務的意見》，指出“研究制定學生發展核心素養體系和學業質量標準”［7］.在此之后，有關核心素養的研究猶如雨后春筍般出現，而且大多數的落腳點都是如何培養學生的數學核心素養.比如在數學文化領域，也在思考數學文化如何促進數學核心素養的發展？具體有哪些途徑？那不免也會將數學思想方法和核心素養之間聯系起來，史寧中教授提到數學基本思想與數學“雙基”“四基”、數學核心素養都是一脈相承的，基于“四基”的數學教學就是基于數學核心素養的數學教學［8］.因此數學思想方法與數學核心素養有著不可割裂的聯系.但從圖3可以看出，“數學思想方法”“數學核心素養”這兩個領域關鍵詞的距離較遠，說明其相關性不高，研究者常忽略之間的關系.所以通過“數學解題”這一橋梁，在解題中滲透數學思想方法，從而促進數學核心素養的發展是未來探究的方向.

3.2 不等式問題探究

從圖2可以看出，領域3的研究熱點以不等式為中心，說明數學中的解題思路，解題技巧，解題方法都能從不等式問題入手，在解不等式過程中滲透著許多數學思想方法，而且不等式在數學解題中也有廣泛的應用.安振平老師提出了二十六個優美不等式［9］，引來了很多讀者探討.其中李建潮利用配偶法證明第1個不等式［10］；何業亮利用齊次化的解題技巧對其中第5個給出了簡潔證法［11］；李雙娥利用極化恒等式證明其中第19個不等式［12］；查正開運用數學歸納法證明第21個不等式［13］；王煒利用換元法證明其中第23個不等式［14］；蘇建國利用函數思想證明其中第14、17、18和第19個不等式［15］；衛福山通過適當的變換，利用三角不等式“變”出很多代數不等式證明其中第5、6、7和第25個不等式，這其實就是化歸的思想方法［16］.不等式在數學解題中的應用也比較廣泛，如用基本不等式求最值，柯西不等式在幾何中的應用.這足以說明不等式在數學解題中有著很高的戰略價值，而優美不等式不僅僅只有這二十六個，同一不等式可以尋找新的通識解法，不等式中所展示的解題思路，解題技巧以及所滲透數學思想方法值得去深度探究.

3.3 波利亞中的元認知思想

在圖2中可以看出，領域1中的“元認知”“問題解決”“數學思維”“策略”“審題”等關鍵詞在第四象限，而這幾個關鍵詞主要圍繞元認知展開.元認知是指人們對自己認知的認識［17］，如解一道題過程，審題，思考解題思路，解題后反思都屬于元認知.數學元認知在數學認知過程中具有重要作用，主要體現在數學問題解決、數學思維、數學學業成績三個方面［18］.而如何培養元認知能力，則可以從波利亞元認知思想著手.因為波利亞解題思想不僅是一種解題策略，也是一個完整的元認知體系.“怎樣解題表”給出的“提示語”就是典型的元認知知識［19］.譬如，“未知量是什么？已知數據是什么？條件是什么？”、“你知道一道與它有關的題目嗎？”、“你知道一條與它有關的定理嗎？”［20］等等.這些提示語都不直接拿來解題，而是在合適的時機給予正確的引導.因而在解題時經常自覺地運用這些提示語，是提高解題元認知能力的有效途徑.因此，波利亞思想中含有豐富的元認知論述，是研究數學元認知的思想寶庫［21］.但是除了波利亞中的元認知思想，其他數學家中的數學思想是否也有著元認知思想？這值得去關注和發現.另外，在教學中，教師還能引導學生總結自己的提示語，這樣學生不僅印象深刻，而且學生的元認知能力也得以提高.

3.4 注重解題教學中反思能力

波利亞在“怎樣解題表”中將解題過程分為四個階段：理解題目，擬定方案，執行方案，回顧［20］.然而在教學實踐中往往只注重了前三個環節，而忽視了最后的一個環節——回顧，有些甚至于把解題教學直接演變為“題海戰術”［22］，學生也逐漸喪失學習數學的興趣.王華老師認為，解決數學問題有三種境界：就題論題，就題論法，就題論道［23］.第一種境界就是解一道題，會一道題，每道題都是獨立的存在；第二種境界就是通過這道題學會了解決問題的一般方法，能舉一反三；第三種境界是解一道題，總結了一條規律，發現問題的本質.因此，教師如果只教一道題，學生就只會一道題；教師能歸納總結出問題的一般方法，學生也能觸類旁通；教師如果不會反思，也教不出會反思的學生.所以教師首先要加強自身反思能力，在解題教學中提高學生的反思水平，爭取做到“就題論道”［24］.在圖2中，領域2中“解題反思”和“一題多解”形成了“解題反思：一題多解”研究領域，一題多解就是一種很重要的解題后的反思.首先對于同一個問題，當一種解法完成后，經過回顧思考，去尋找另一種解法，一種更加簡潔的方法.再進一步反思尋找不同解法之間的聯系，總結共性，這也是多解歸一.其次，會了一道題，更要學會觸類旁通，相似的題要聯系起來，尋找共同規律，歸納總結出一類題型；最后，再回到題目本身，可以通過改變條件，轉換問題形式，也就是常說的變式訓練，讓學生更能掌握問題的本質.

4 結論與展望

對20年來有關數學解題的學術期刊論文和碩博士論文進行了系統梳理，對數學解題領域的研究熱點有了更直觀的了解，研究中所呈現的問題也值得關注：首先，如何讓“數學解題”作為載體，使數學思想方法促進數學核心素養發展；其次，不等式在數學解題中有著非常重要的地位，從簡單到復雜，每一個不等式所帶來的思路、技巧以及蘊含的數學思想方法都值得去深度剖析；然后數學元認知對數學解題也有著重要的作用，除了波利亞思想中含有的豐富元認知論述以外，其他數學家思想也值得挖掘、探究，從而培養元認知能力；最后在解題過程中往往會忽略總結反思環節，教師應該從自身做起，帶領學生一起進行一題多解、多解歸一、多題歸一的實踐，從而在解題教學中提高反思能力.

參考文獻：

［1］ 中共中央辦公廳國務院辦公廳.關于進一步減輕義務教育階段學生作業負擔和校外培訓負擔的意見［J］.中華人民共和國國務院公報，2021（22）：149.

［2］ 張奠基，宋乃慶.數學教育概論（第三版）［M］.北京：高等教育出版社，2016.

［3］ 羅增儒，羅新兵.作為數學教育任務的數學解題［J］.數學教育學報，2005（1）：125.

［4］ 單壿.解題研究［M］.上海：上海教育出版社，2016.

［5］ 張楠，宋乃慶，黃新，etal.國際STEAM教師研究的熱點與發展趨勢——基于VOSviewer的文獻計量分析［J］.開放教育研究，2020，26（5）：7887.

［6］ 郭文斌，聶文華.我國隨班就讀研究熱點及發展趨勢［J］.現代特殊教育，2021（9）：1723.

［7］ 《關于全面深化課程改革落實立德樹人根本任務的意見》節選［J］.教育科學論壇，2017（20）：35.

［8］ 劉祖希.訪史寧中教授：談數學基本思想、數學核心素養等問題［J］.數學通報，2017，56（5）：15.

［9］ 安振平.二十六個優美不等式［J］.中學數學教學參考：上半月高中，2010（1）：136.

［10］ 李建潮.配偶法證明“第一個”優美不等式［J］.河北理科教學研究，2016（5）：4344.

［11］ 何業亮.一個優美不等式的簡潔證法［J］.中學數學教學，2018（1）：52.

［12］ 李雙娥.簡證第19個優美不等式［J］.數學學習與研究，2017（21）：142.

［13］ 查正開.第二十一個優美不等式的證明與推廣［J］.數學教育研究，2012（4）：46.

［14］ 王煒.用換元法證明不等式——第23個優美不等式的別證和推廣［J］.數學教學通訊，2018（9）：7778.

［15］ 蘇建國.幾個優美不等式的統一證明和推廣［J］.數學教育研究，2012（1）：6364.

［16］ 衛福山.幾個優美不等式的淵源及證明［J］.中學數學：高中版，2012（5）：7273.

［17］ 袁文斌.談元認知理論在數學解題過程中的作用［J］.社會科學家，2007（S1）：1545.

［18］ 歐慧謀，唐劍嵐.國內數學元認知的研究與思考［J］.課程·教材·教法，2012，32（5）：5861.

［19］ 涂榮豹.數學解題學習中的元認知［J］.數學教育學報，2002（4）：611.

［20］ G·波利亞.怎樣解題［M］.上海：上海科技教育出版社，2011.

［21］ 徐伯華，朱鳳琴.論波利亞的元認知思想［J］.數學教育學報，2008（3）：1416.

［22］ 王宏賓，羅增儒.例談解題回顧的意義［J］.數學教學，2007（5）：36.

［23］ 王華.由如何獲得梯形底邊上的中點談起［J］.數學教學，2009（1）：1819.

［24］ 陳永明.數學習題教學研究［M］.上海：上海教育出版社，2014.