試析高中數學命題教學中的先行組織者*

廣東省廣州市花都區教師發展中心 (510800) 李桃

《普通高中數學課程標準(2017 年版2020 年修訂)》中指出: 教師要把教學活動的重心放在促進學生學會學習上,積極探索有利于促進學生學習的多樣化教學方式;教師要善于根據不同的內容和學習任務采用不同的教學方式,優化教學,抓住關鍵的教學與學習環節,增強實效[1]. 美國教育心理學家奧蘇貝爾提出的先行組織者理論旨在構建能激發學生主動學習的有意義學習,恰好契合新課程所倡導的教學理念.

1 先行組織者的內涵

奧蘇貝爾首次給出“先行組織者”的經典定義: 先于學習材料之前呈現的,在概括與包容水平上高于新的學習材料的引導性材料. 他認為先行組織者要比新材料要更具抽象性、概括性和綜合性,并能清晰地反映學生認知結構中原有的知識原式與新的學習任務之間的聯系[2]. 奧蘇貝爾本人以及后來的研究者發展了這一概念使之更加寬泛, 在呈現順序上,先行組織者不僅可以在學習新材料前呈現,也可以在過程中和之后呈現;在包攝性上,先行組織者既可以高于學習材料,也可以低于學習材料. 但都要求先行組織者與新知識有實質性的聯系,并能促進新知識的學習、保持[3].

2 高中數學命題教學

所謂數學命題,指的是數學真命題,其外延就是數學課程中的數學公理、定理、數學公式、法則、數學對象的性質等.根據廣義知識學習三階段(習得、鞏固和轉化、遷移和運用)模型,命題習得階段包含注意與預期、命題獲得兩個環節. 喻平教授指出命題獲得的基本模式包含結果型、發生型和問題解決型[4]. 根據高中數學命題的特點及教學要求,高中數學命題獲得的常用模式是問題解決型和發生型(見圖1、圖2).

圖1: 提出問題→解決問題→獲得命題

問題解決型命題教學模式,其基本思想是把命題還原為一個抽象的數學問題,通過解決問題而得到命題的教學模式.解決問題的過程對于發展學生的批判思維,提高邏輯推理能力,培養學生的創新意識有積極作用.

圖2: 先行組織者→推理→證明→獲得命題

發生型命題教學模式,其基本思想是引導學生去經歷知識產生的過程,為形成命題域和命題系建立認知基礎. 常用策略是設計先行組織者,引導學生去感知、體驗、概括、抽象,從而歸納出命題,再分析證明思路,寫出證明過程. 這一教學模式有利于培養學生的歸納推理能力、邏輯推理能力等.

3 命題教學中的先行組織者

結合國內外對先行組織者的研究成果及實踐思考,課題組對先行組織者作出大致的分類. 按照引導性材料在命題教學過程中發揮的教學功能,將先行組織者分為導學性、導思性、導知性、整合性這四類;按照其呈現形式,進一步細分有陳述式、問題式、任務式先行組織者. 接下來,筆者以命題習得階段的兩個環節及鞏固階段為主線,通過五個教學案例對各類先行組織者的內涵進行闡述,與專家同行交流.

3.1 導學性先行組織者

在命題習得階段的注意與預期環節,為激發學生對一個單元、一節課或一個知識點產生積極的學習心向,幫助學生建立新舊知識的聯系,促進學生對知識的主動建構,為此所設計的引導性材料統稱為導學性先行組織者,分為導學任務式、導學陳述式.

3.1.1 導學任務式

這種導學任務式先行組織者是基于新舊知識的聯系而提出的學習任務,能引起學生的認知沖突. 一方面,藉此可以激發學生對學習新知識的預期,另一方面,這種聯系對新知識的探索具有導向作用.

案例1 “兩角差的余弦公式”教學片斷

教師布置任務: 已知α為任意角,請將以下式子進行化簡.

學生利用誘導公式能夠將①②兩個式子化簡, 對于③④兩個式子有著多種不確定的猜測. 教師引導學生認識: (1) 運用誘導公式有特殊限制, 有必要去探索任意兩角差公式. 此時, 教師提出本節課的中心問題: 對于任意角α,β,cos(α-β)與α,β的三角函數值有什么聯系? (2)誘導公式是任意兩角差公式的一類特殊情形. 基于這樣的聯系,可以將探索誘導公式的經驗遷移運用到探索任意兩角差余弦公式[5].

3.1.2 導學陳述式

這種導學陳述式先行組織者是教師呈現給學生的一段材料(文字、圖表、視頻等),幫助學生建立對本單元或本節課(其中包括內容結構、基本思想和特點等)的整體性認識. 這種整體性認識隨著學習的深入,學生將習得的知識置于初期輪廓的適當位置歸類并固定下來,這樣既可以促進新的學習開始,又可以防止歸類以后的消失,這有助于學生良好認知結構的形成和發展.

案例2 “平面向量及其應用”教學片斷

教師指導學生閱讀教材上的章節引言, 學生可以明確:(1)本章的研究對象: 平面向量(既有大小又有方向);(2)研究內容: 概念;運算法則及運算性質;應用;(3)研究方法: 類比、數形結合等.

3.2 導思性與導知性先行組織者

在命題習得階段的獲得環節,為促進學生主動思考探索,積極參與獲得知識的過程,在問題解決型、發生型命題獲得模式中設計的引導性材料分別統稱為導思性、導知性先行組織者.

3.2.1 導思性先行組織者

對于問題解決型命題獲得模式,關鍵是啟發學生找到解決問題的方法. 當問題難以直接解決時,教師要根據學生認知水平設計恰當的導思性先行組織者. 學生經歷完成一項具體任務,或者通過閱讀一段材料,從中抽象概括出解決問題的方法,再將方法遷移運用到解決一般問題. 對應的任務、材料分別稱為導思任務式、導思陳述式先行組織者.

案例3 “等差數列前n 項和公式”教學片斷,2 種技術路線

(1)導思任務式

教師在提出本節課的研究主題后,給出求具體的等差數列之和的任務為先行組織者.

如下圖所示,建筑工地上堆放著一堆鋼管,最上面一層有4 根,下面每一層比上一層多一根,共7 層,請計算這一堆鋼管的總數.

（49）伏願神明如在，盻蠻來臨。鑒此際之精虔，削多生之罪對。（《北極真武佑聖真君禮文》，《中華道藏》30/587）

學生用算術的方法很容易得到運算結果,教師引導學生觀察圖形,學生容易觀察到梯形區域中的部分區域是平行四邊形,這部分容易計數. 教師順勢讓學生回顧梯形與平行四邊形的關聯. 梯形面積公式的推導采用“平行倒置”的策略.學生將形的“倒置”遷移到數式的“倒序”,可自行推導出等差數列前n項和公式

(2)導思陳述式

教師在提出本節課的研究主題后,呈現以下閱讀材料為先行組織者.

我國南宋數學家楊輝提出了這樣一個問題:“今有圭垛草一堆,頂上一束,底闊八束,問共幾束? 答: 36 束. ”他的計算方法可以用下圖來表示.

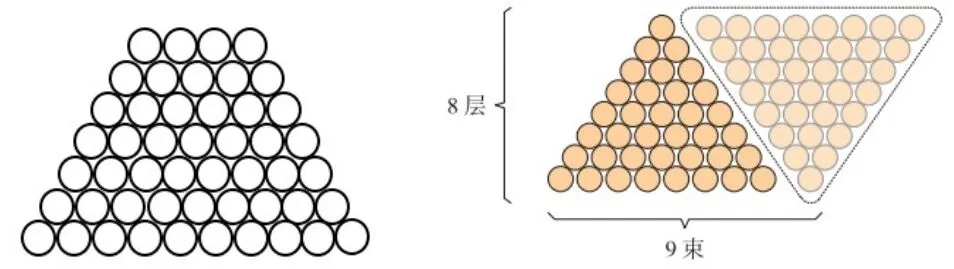
楊輝設想有另外一堆同樣的草,將其倒置,并和原來的草堆拼在一起,這就得到8×9 的草堆,一共72 束,因此原來的草堆共有36 束. 學生通過分析計數方法,可明確關鍵因素是各行的數量依次構成等差數列,即可采用“平行倒置”的策略計數. 學生將形的“倒置”遷移到數式的“倒序”,可自行推導出等差數列前n項和公式

3.2.2 導知性先行組織者

對于發生型命題獲得模式,關鍵是設計出符合邏輯,適切的導知性先行組織者. 學生在問題鏈的啟發下,逐步發現新命題,或者發現新舊命題之間的聯系,由舊命題推理得到新命題; 又或者學生根據閱讀材料(操作實驗)歸納出新命題. 對應的問題鏈、廣義的閱讀材料(操作實驗)分別稱為導知問題式、導知陳述式先行組織者.

案例4 “對數函數的圖象與性質”教學片斷,2 種技術路線.

教師設計以下問題鏈:

問題1. 從運算的角度看,同底的對數函數與指數函數有怎樣的聯系?

問題2. 以上聯系反映到兩者的函數圖象上有什么幾何意義?

學生根據兩個函數的自變量與函數值的關聯,由點的對稱可知同底的指數函數與對數函數的圖象關于直線y=x對稱. 由此,學生可以根據指數函數圖象作出同底的對數函數的大致圖象,進而對照指數函數的圖象與性質,梳理出對數函數的圖象與性質.

(2)導知陳述式

利用計算工具畫圖,將底數a作為變化的控制量,教師

給學生演示動態圖象或者學生動手操作. 學生觀察這些圖象的位置、公共點和變化趨勢,類比指數函數的圖象與性質,歸納出對數函數的圖象與性質.

3.3 整合性先行組織者

在命題鞏固階段,教師引導學生辨別新舊命題的區別與聯系,利用學習任務幫助學生形成命題域、命題系,這都有利于學生將新舊知識整合到認知體系中, 不斷完善認知結構,促進記憶的保持和增進. 這類學習任務或問題統稱為整合性先行組織者.

案例5 “基本不等式”教學片斷

由重要不等式推導出基本不等式后,教師布置以下2 個學習任務.

任務1: 在圓O中,AB是圓的直徑,點C是AB上的動點,AC=a,BC=b. 過點C作垂直于AB的弦DE,連接AD,BD. 請在這個圖形中對基本不等式進行解釋說明.

學生完成任務1,則獲得基本不等式的幾何表征,直觀形式有助于學生理解記憶這個命題.

任務2: 已知a,b∈R,請證明

學生完成任務2,一方面,基本不等式與這個常用不等式組成一個命題域,幫助學生形成系統的認知結構,另一方面,教師引導學生對從試誤到頓悟的解答過程進行反思,有利于深化學生對基本不等式與重要不等式的準確認識.

結束語

在高中數學命題教學中,教師應以課程標準中對命題的教學要求和學生認知水平為依據,制定恰當的命題教學方案,以促進學生主動參與命題的學習過程;以深刻理解命題本質為目的,合理設計先行組織者,發揮好先行組織者的橋梁作用、導向作用,切實提升命題教學的實效,發展學生的核心素養.