善用轉化思想化解圓錐曲線中的運算難點*

廣東省中山市桂山中學 (528463) 林娜

解析幾何一直是高考重點考查的內容,也是一個難點內容,是高考的一塊“硬骨頭”. 解析幾何問題的難主要體現在運算上,大部分學生在繁瑣和復雜的運算中找不到運算的方向,喪失了信心,也丟掉了寶貴考試時間和分數. 其實運算的難很大一部分原因是我們沒有找到合適的運算途徑和方向,沒有學會轉化,如果我們能夠善用轉化思想,將復雜的陌生的問題轉化為簡單的熟悉的問題,我們就能夠找到合適的運算途徑和方向去化解圓錐曲線中的一些運算難點.

1 準備知識

以上結論是圓錐曲線中的常見二級結論,由于篇幅的限制,證明過程略,詳細證明過程讀者可查看參考文獻.

接下來我們通過一些典型的例題來展示轉化思想在化解圓錐曲線中的運算難點時所發揮的作用.

2 典型問題

2.1 轉化為中點弦問題

點評本題的解決方法有很多(讀者可自行研究),通常的做法是將面積的比例關系轉化為坐標關系,然后經過變形可以用韋達定理將條件表達出來,最后將韋達定理代入,得出結論,中間的運算過程比較復雜,也需要花費較多時間. 經過轉化后,我們看清楚了這道題所給條件的本質,本質就是PQ的中點與MN的中點重合,再結合直角三角形的性質和中點弦的結論,很容易得到正確答案.

2.2 轉化為斜率之積為定值

2.3 轉化為斜率之和為定值

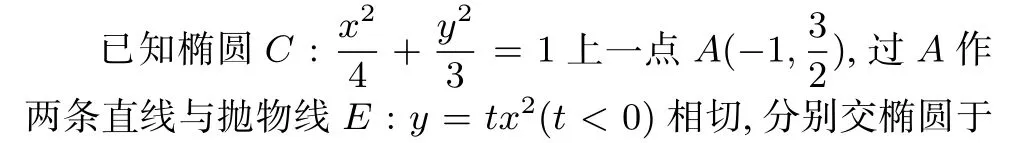
2.4 轉化為坐標之比

(2019 年浙江卷)如圖,已知點F(1,0) 為拋物線y2=2px(p＞0) 的焦點, 過點F的直線交拋物線于A,B兩點, 點C在拋物線上, 使得ΔABC的重心G在x軸上,直線AC交x軸于點Q,且Q在點F右側. 記ΔAFG,ΔCQG的面積為S1,S2.

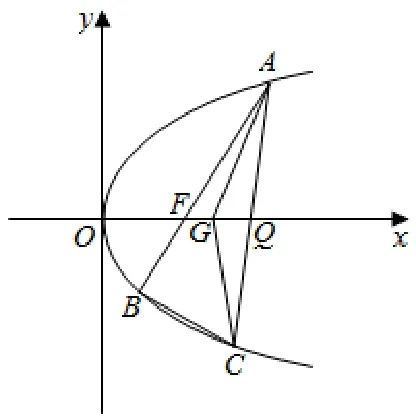
2.5 轉化為向量的數量積

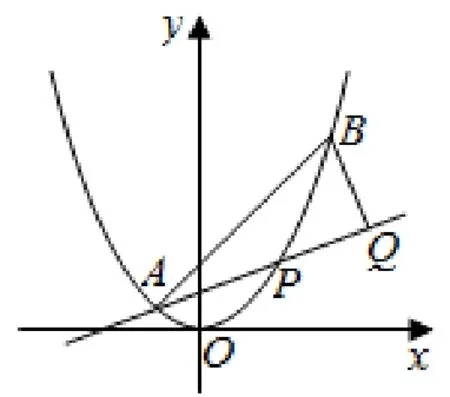
3 鞏固練習

4 教學反思

帶領學生閱讀相關文獻資料,證明儲備知識的結論,再把相關的轉化思想應用于不同的題目,在課堂中很好的實現了文獻閱讀與寫作的數學教學內容,讓學生通過文獻閱讀實現舉一反三,授之以魚,不如授之以漁. 今后也可提供給學生優秀的閱讀材料,讓學生去寫閱讀啟示,以及同類問題的解決方法等. 僅以本文給學生以示范,本課例應該作為單元教學設計,設計3 或4 個課時去完成,這節課為學生碰到新的圓錐曲線問題提供了方法上的指引,以至于不再畏懼冗長復雜的各種圓錐曲線第二問.