基于作業軌跡約束的機械臂多閉環標定方法

蔣周翔，秦鵬舉，蘇瑞，龍忠杰，宋寶，唐小琦

(1.北京信息科技大學機電工程學院，北京 100192；2.華中科技大學機械科學與工程學院，湖北武漢 430074)

0 前言

機械臂末端絕對定位精度是評價機械臂技術水平的重要指標，是能否準確完成抓取、裝配、加工等作業任務的主要決定因素之一[1]。補償連桿 (Denavit-Hartenberg，DH)參數誤差是提高機械臂絕對定位精度的有效方式，關鍵問題之一是如何選取合適的測量構型進而建立良態辨識模型[2]，如此才能保證DH參數誤差的準確求解。

目前常采用的測量構型主要分為開環和閉環2類[3]。其中，開環是指機械臂末端不受物理約束，允許在整個運動空間中選擇測量構型。閉環是指機械臂末端受到物理約束，要求在末端名義位置基本不變的前提下選擇測量構型。通常來講，開、閉環構型方案的選擇與測量裝備的選擇密切相關。例如，若采用Faro或Leica激光跟蹤儀[4-5]或立體視覺[6-7]作為測量手段，則往往選用開環方案，原因是激光跟蹤儀和雙目相機具備較大的測量范圍，并沒有嚴格限制機械臂末端運動。如若采用雙球桿儀[8]、觸發式測頭[9]或激光位移傳感器[10]，則通常采用閉環方案，原因是這些測量設備的量程很小，要求機械臂末端只能在極小空間內運動。選定開環和閉環方案后，下一步需要確定具體的測量構型。目前一部分學者采用隨機方式生成測量構型，另一部分則以辨識模型觀測指數或條件數為優化目標，選用DETMAX等優化算法來選擇測量構型[11-13]。還有學者在此基礎上額外考慮了傳感器的可視性對構型選擇的約束[14]。研究表明：優化后的構型比隨機構型能達到更高的DH誤差辨識精度。

上述方法在面向實際工程應用時，在以下幾個方面還需研究與改進：

(1)傳統的開環方案在選擇測量構型時具有更好的靈活性，但對運動空間的完整性要求更高，這通常與實際應用中的非結構工作環境相矛盾，降低了該類方案的實用性。

(2)傳統的閉環方案雖然僅需較小的運動空間，但末端物理約束過于嚴格，導致測量設備安裝調試難度較大，制約了此類方案的推廣和應用。

(3)現有的開環、閉環方案得到的測量構型難以與機械臂實際作業軌跡保持一致，迫使機械臂停工來配合末端位姿采集，因此降低了生產效率，增加了維護成本。

面對上述現狀，本文作者采用新方法，以雙目相機作為測量設備，以機械臂實際作業軌跡為主要約束條件、以辨識矩陣形態水平為優化目標規劃測量構型，并在此基礎上生成新作業軌跡。當機械臂精度衰減至需要標定時，執行新作業軌跡并實時測量末端位姿，即可建立辨識模型解出DH參數誤差用于關節指令補償。新方法將視覺采集、作業軌跡與閉環方案相融合，既突破了閉環測量的強物理約束，又利用了閉環測量時末端點位相對集中的特點，由此提出的基于作業軌跡約束的多閉環測量方案使機械臂實時標定成為可能。

1 機械臂多閉環標定系統的設計

標定系統框架與流程如圖1所示。

圖1 標定系統框架與流程

圖1中系統運作流程為：

(1)在工作軌跡上選取N個測量點；

(2)以各測量點位姿和傳感器有效采集為約束條件，以辨識模型性態水平為優化目標，選擇Nm1個測量構型；

(3)圍繞測量構型重新規劃若干條平滑的標定-作業共用軌跡；

(4)機械臂先按照原始作業軌跡進行作業，傳感器實時監控末端位姿；

(5)當位姿誤差超過閾值時，機械臂開始以新軌跡進行作業，即以選取的測量構型經過對應的測量點，同時傳感器采集機械臂末端位姿，輸入至上位機；

(6)在經過各測點時，機械臂控制系統同步發送關節指令至上位機；

(7)由上位機求出所有測量構型對應的末端位姿誤差和辨識矩陣，并建立辨識模型，解算出DH參數誤差；

(8)誤差值輸入至控制系統進行補償進而提高機械臂末端位姿精度。

2 機械臂坐標系的建立

機械臂坐標系分布如圖2所示。

圖2 機械臂關節坐標分布

圖2中：{Xi，Yi，Zi}為第i關節坐標系的3個坐標軸，i=1，2，…，6；{X0，Y0，Z0}為基坐標系；{Xt，Yt，Zt}為靶標坐標系。機械臂末端名義位姿是通過正運動學計算得到的，具體是采用式(1)所示齊次變換矩陣相乘：

0Tt=0T11T22T33T44T55T66Tt

(1)

式中：0Tt為機械臂基座標系到末端靶標坐標系的齊次變換矩陣；i-1Ti為第i-1關節坐標系到i關節坐標系的齊次變換矩陣。i≠2時，i-1Ti為

i-1Ti=Rz(θi)Tz(di)Tx(ai)Rx(αi)

(2)

而i=2時，i-1Ti為

1T2=Rz(θ2)Tx(a2)Rx(α2)Ry(β2)

(3)

6Tt為第6關節坐標系到末端傳感器坐標系的齊次變換矩陣。6Tt表示為

6Tt=Tx(xt)Ty(yt)Tz(zt)Rx(αt)Ry(βt)Rz(γt)

(4)

式中：Rx(*)、Ry(*)、Rz(*)為旋轉矩陣；Tx(*)、Ty(*)、Tz(*)為平移矩陣；{θi，di，ai，αi}為第i關節的標準DH參數；{xt，yt，zt，αt，βt，γt}為傳感器安裝參數；β2為針對相鄰平行關節而增加的偏轉角，目的是在機械臂標定中保持DH參數的數值連續性[15]。

3 機械臂DH誤差辨識模型的建立

令{δθi，δdi，δai，δαi，δβi}為DH參數誤差，ΔσDH，i表示i關節DH參數誤差的向量，則有：

將所有ΔσDH，i按關節順序合并得到：

ΔσDH=[ΔσDH，1，ΔσDH，2，…，ΔσDH，6]T

假定機械臂建立辨識模型共需M個測量構型，令{δxj，δyj，δzj，δαj，δβj，δγj}為第j個測量構型對應的傳感器坐標系位姿偏差分量，則位姿偏差ΔEj為

ΔEj=[δxj，δyj，δzj，δαj，δβj，δγj]j=1，2，…，M

其中，各位姿偏差分量計算式如下：

(5)

式(5)中的元素來源于傳感器名義坐標系到實際坐標系的齊次變換矩陣：

(6)

式中：0Ttnj、0Ttaj分別為第j個測量構型對應的傳感器名義坐標系矩陣和實際坐標系矩陣。

將M個測量構型對應的ΔEj合并得到：

ΔE=[ΔE1，ΔE2，…，ΔEM]T

(7)

再結合微分變換原理和機械臂正運動學，可建立ΔσDH到ΔE的線性映射關系：

ΔE=JΔσDH

(8)

若用J+表征雅克比矩陣J的廣義逆，則由上式可建立機械臂DH參數誤差的辨識模型：

ΔσDH=J+ΔE

(9)

4 測量構型的確定

4.1 建立測量構型庫

測量構型庫的建立分為2個步驟：首先是在原作業軌跡上選擇若干測量點，并以各測量點坐標為約束求運動學逆解，以此得到若干測量構型；然后在每個測量構型下檢驗靶標是否能被相機有效采集，將不滿足要求的構型剔除，得到初始的測量構型庫。下面分別對2個步驟進行闡述：

(1)以測量點作為約束

測量點選取的原則首先是該點位處光照穩定，這是視覺系統準確采集的前提。此外，還應盡量使測量點間隔均勻，以保證點位具有一般性。

令選擇的測量點在基坐標系下的位置為[pxk，pyk，pzk]T，其中k=1～N。在±π范圍內均勻取m個值，由3組m個角度值交叉組合生成m3個不同的角度組合[α6，β6，γ6]T，與[pxk，pyk，pzk]T組合成Nm3個靶標位姿向量[px，py，pz，α6，β6，γ6]T，然后由齊次變換運算得到每個位姿向量對應的靶標坐標系矩陣0Tt。最后通過機械臂逆運動學求出所有0Tt對應的關節指令集合{θ1，θ2，θ3，θ4，θ5，θ6}q1，其中q1=1～Nm3。

(2)以靶標的可視性作為約束

令靶面法向量為靶標坐標系Zt軸向量，計算每個0Tt的Zt軸與相機光軸(Zc軸)間夾角θq1。由于θq1∈[-π/2，π/2]對應的靶標姿態無法被相機識別，因此與之對應的測量構型不符合標定要求，將它剔除后得到測量構型庫{θ1，θ2，θ3，θ4，θ5，θ6}q2。

4.2 測量構型優化

采用DETMAX方法，在測量構型庫{θ1，θ2，θ3，θ4，θ5，θ6}q2中進行篩選，最終得到能夠用于標定的測量構型{θ1，θ2，θ3，θ4，θ5，θ6}q3。

DETMAX方法的基本步驟是：

(1)在構型庫中初選q個構型組建對應的辨識矩陣Jq，其維度為6q×24；

(2)計算其觀測指數O1(q)；

(3)在剩余q2-q個構型中任選一個構型建立J1，與Jq組成Jq+1，其維度為6(q+1)×24，并計算其觀測指數O1(q+1)；

(4)若O1(q+1)>O1(q)， 則保留添加的構型，否則棄置，該構型不再回到測量構型庫中；

(5)從q+1構型中減去除新添加構型之外的其他任一構型，建立辨識矩陣Jq′并計算其觀測指數O1(q′)；

(6)若O1(q′)>O1(q+1)則刪除該構型，否則保留，該構型不再回到剩余構型庫中；

(7)對所有剩余的q2-q個構型均依次執行步驟(3)—(6)，最終得到測量構型{θ1，θ2，θ3，θ4，θ5，θ6}q3及其對應的辨識矩陣Jq3。

4.3 由測量構型生成新作業軌跡

開環方案的測量構型彼此差異明顯，然而閉環方案的機械臂末端運動受到約束，因此部分構型較為近似，可通過K-means聚類分析法得到若干構型簇{Θ1，Θ2，…，ΘK}。每個簇內的測量構型相對接近，與機械臂指定任務點(完成抓取、裝配等任務的點位)的構型結合，輸入至機械臂控制系統，即可規劃K條新作業軌跡。

機械臂開始作業后，預先架設好的雙目相機持續采集末端靶標位姿。當發現位姿精度衰減超過設定閾值時，機械臂不再執行初始作業軌跡，而是依次沿K條新作業軌跡完成工作任務。機械臂途徑新作業軌跡的N個測量點時，雙目相機實時采集靶標位姿，與對應的靶標名義位姿以及測量構型{θ1，θ2，θ3，θ4，θ5，θ6}q3結合，即可建立式(9)所示辨識模型。

5 仿真驗證

5.1 確定測量點

首先為機械臂DH參數設定如表1所示的名義值用于建立其運動學模型，與之對應的機械臂關節坐標系布局與圖2一致。第6關節坐標系到靶標坐標系的平移和旋轉如表2所示，由此可根據式(4)得到變換矩陣6Tt。

表1 機械臂DH參數賦值

表2 第6關節到靶標的坐標系變換矩陣賦值

至此可指定測量點。為滿足測量點間隔均勻和一般性要求，在各關節旋轉范圍內均勻取4個轉角值，得到各關節指令如表3所示。根據式(1)得到與測量點對應的機械臂名義位姿如圖3所示。

表3 所選測量點對應的關節指令 單位：rad

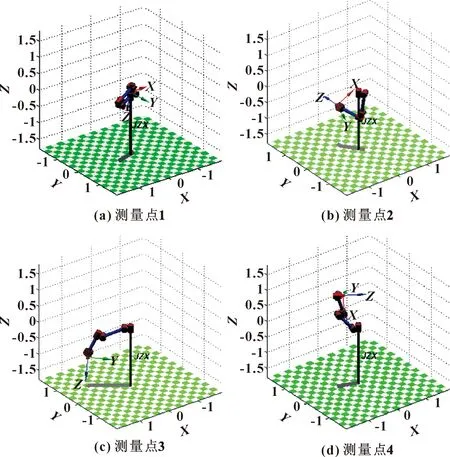
圖3 機械臂姿態

5.2 建立測量構型庫

令第4.1節中的m=10，在每個測量點處得到1 000個靶標位姿向量及其對應的變換矩陣0Tt。再通過機械臂逆運動學求得所有0Tt對應的共4 674個有效可達的關節指令集合{θ1，θ2，θ3，θ4，θ5，θ6}q1。然后以靶標可有效采集作為約束條件，進一步從中篩選出1 930個可行的關節指令集合{θ1，θ2，θ3，θ4，θ5，θ6}q2，并用DETMAX算法從中挑選出24個測量構型{θ1，θ2，θ3，θ4，θ5，θ6}q3。

最后采用K-means算法將24個測量構型進行聚類，使同類別構型的關節指令差別相對較小，以便于機械臂控制系統生成平滑的新作業軌跡。令K=6，構型聚類結果如圖4—9所示。

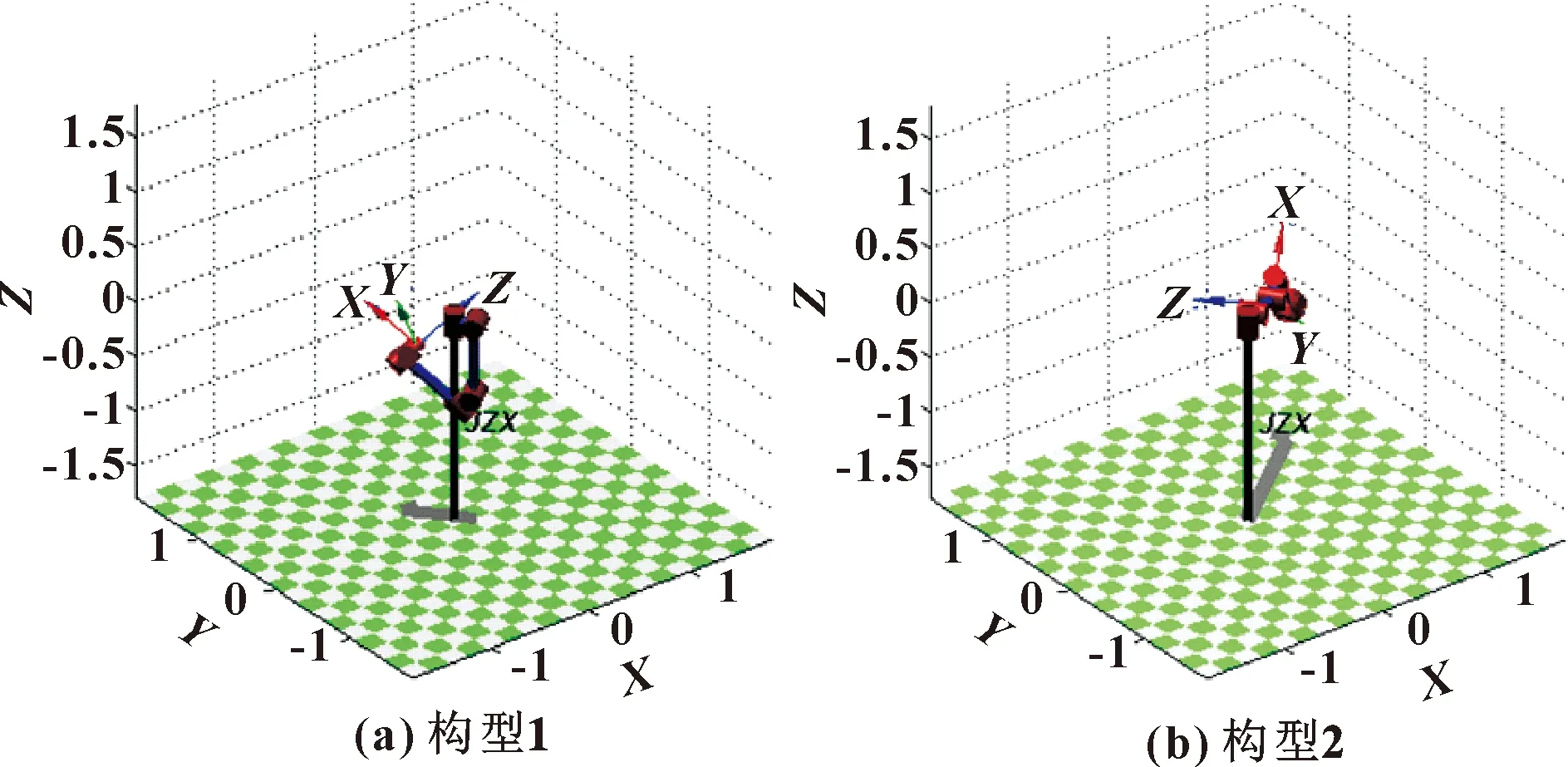
圖4 第1類測量構型

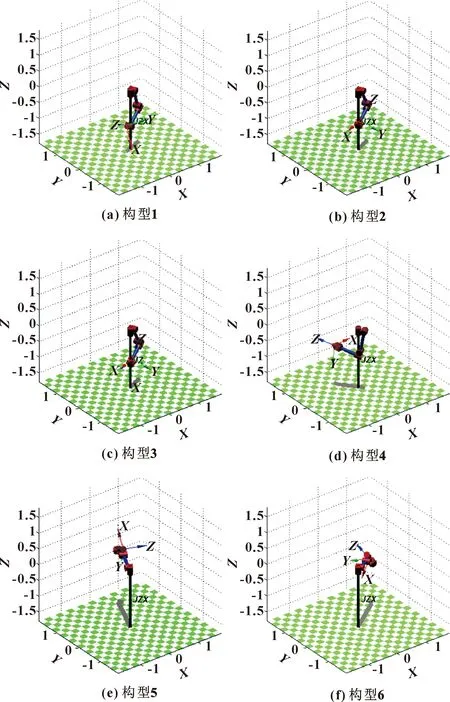
圖5 第2類測量構型

圖6 第3類測量構型

圖7 第4類測量構型

圖9 第6類測量構型

5.3 建立辨識模型

至此可由式(9)得到J。為進一步提高模型性態水平，采用矩陣平衡法優化矩陣J。首先按下式找出矩陣J各列的最大1-范數C：

(10)

式中：J(：，c)為J矩陣的第c列。然后用下式得到列平衡矩陣B的元素bc，c：

(11)

即可得到列平衡對角陣B：

B=diag(b1，1，b2，2，…，b24，24)

(12)

類似的，找出JB矩陣各行最大1-范數R：

(13)

式中：JB(r，：)為JB矩陣的第r行。然后用下式得到行平衡矩陣A的元素ar，r：

(14)

即可得到行平衡對角陣A：

A=diag(a1，1，a2，2，…，a6M，6M)

(15)

將式(12)(14)(9)相結合即可得到經過矩陣平衡處理后的辨識模型：

ΔσDH=B(AJB)+AΔE

(16)

式(9)和式(16)中的J和AJB2個辨識矩陣的觀測指數和條件數如表4所示。

表4 矩陣平衡前后的辨識矩陣性態指標

可見經過矩陣平衡后，辨識矩陣性態水平得到顯著提升，表明新辨識模型下的靶標位姿誤差能夠更顯著反映出DH參數誤差的影響，且辨識精度對測量噪聲的敏感度明顯降低。

5.4 DH參數誤差辨識精度驗證

令DH參數誤差真實值ΔσDH，i如表5所示。

表5 機械臂DH參數誤差賦值

再根據下式計算出靶標在測量構型處的實際坐標系：

0Ttaj=0T1a1T2a2T3a3T4a4T5a5T6a6Tt

(17)

式中：0Ttaj為在第j個測量構型處的機械臂基座標系到機械臂末端靶標坐標系的實際齊次變換矩陣；i-1Tia表示第i-1關節坐標系到i關節坐標系的實際齊次變換矩陣。其中i≠2時，i-1Tia為

i-1Tia=Rz(θi+δθi)Tz(di+δdi)·Tx(ai+δai)Rx(αi+δαi)

(18)

i=2時，i-1Tia為

1T2a=Rz(θ2+δθ2)Tx(a2+δa2)·Rx(α2+δα2)Ry(β2+δβ2)

(19)

然后由式(1)計算出各測量構型對應的靶標名義變換矩陣0Tt，將它和式(17)所得0Ttaj一并代入式(6)即可得到Δ0Ttj，進而可由式(5)和式(7)得到所有測量構型對應的靶標位姿偏差向量ΔE。

由于新方法擬采用雙目視覺系統，因此根據主流視覺測量設備性能參數，假設采用高性能雙目相機時測量噪聲分布規律如表6所示。

表6 采用高性能雙目相機時測量噪聲分布規律

而假設采用普通雙目相機時，測量噪聲分布規律如表7所示。

表7 采用普通雙目相機時測量噪聲分布規律

(20)

采用表6所示測量噪聲時的DH誤差辨識結果和辨識精度如表8所示。

表8 低測量噪聲下的DH誤差辨識精度

采用表7所示測量噪聲時的DH誤差辨識結果和辨識精度如表9所示。

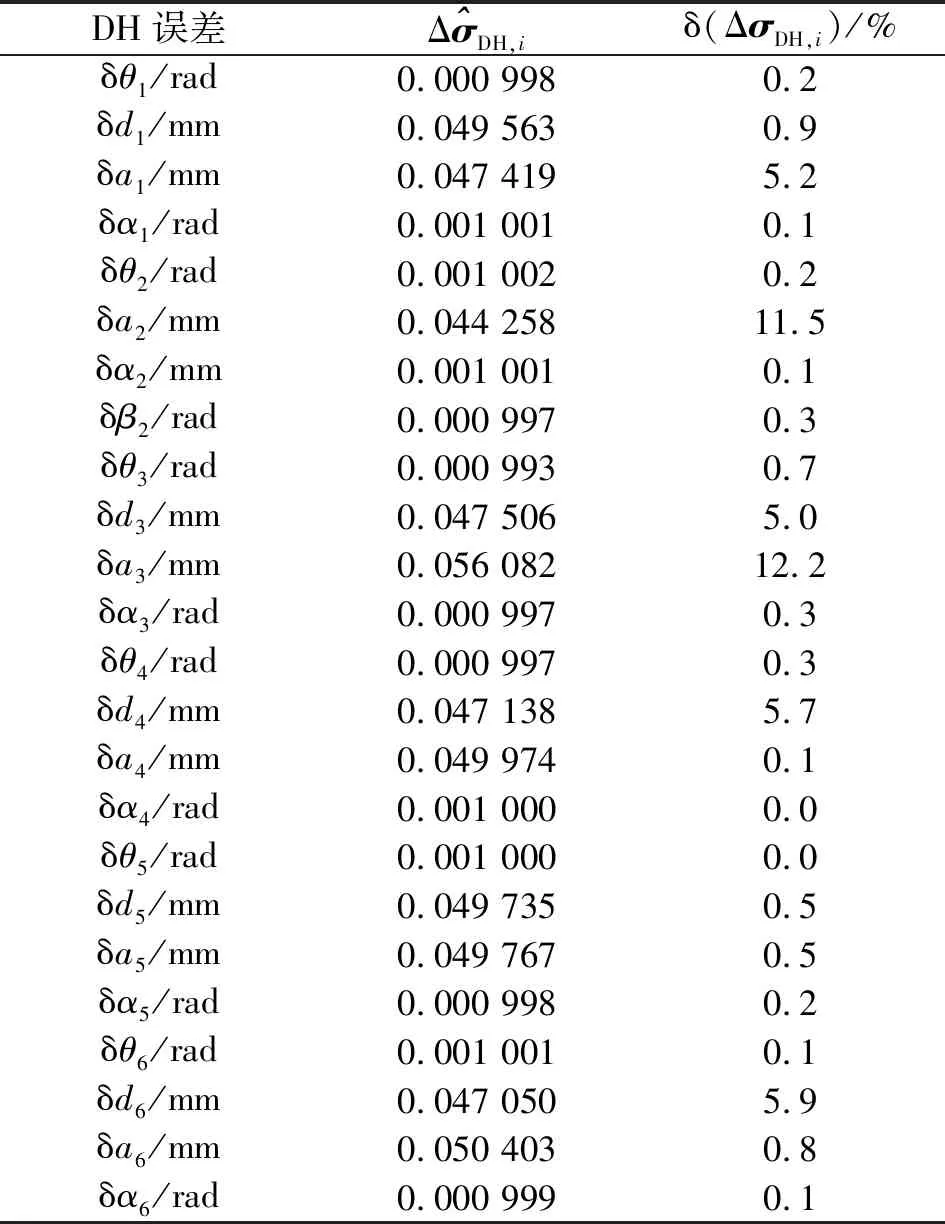
表9 高測量噪聲下的DH誤差辨識精度

結果顯示，低測量噪聲下DH誤差辨識精度在0%～5.1%，其中，角度誤差辨識精度在0%～0.6%，明顯優于距離誤差辨識精度0.1%～5.1%。高測量噪聲下DH誤差辨識精度整體上有所降低，為0%～12.2%，但其中角度誤差辨識精度幾乎沒有變化，為0%～0.7%。與之相比，大多數距離誤差辨識精度無明顯變化，僅δa2和δa3辨識精度降低至11.5%和12.2%，但仍在可接受范圍內。由此可知{δθi，δαi，δβi}相比{δdi，δai}而言，其辨識精度更不易受測量噪聲的影響，這是因為優化后的測量構型能夠使{δθi，δαi，δβi}對末端靶標位姿的影響最大化，而在{δdi，δai}上并不產生類似的倍增效果。此外，距離測量噪聲標準差由0.1/3 mm提高至1/3 mm時，DH誤差平均辨識偏差僅由1.1%增大至1.4%，表明新方法能在不同量級噪聲下維持較高的辨識精度。

6 結語

此研究首先簡單闡述了由微分變換和正運動學理論建立DH誤差辨識模型的原理，再以作業軌跡和靶標可視性作為約束條件生成測量構型庫，并采用DETMAX算法從中挑選出合適的構型用于建立辨識模型，然后提出了一種矩陣平衡方法進一步改善了模型性態水平。為滿足實時標定需求，還采用K-means聚類算法將所選測量構型劃分為若干新作業軌跡。最后通過仿真對新方法的DH誤差辨識精度進行了驗證。

研究結果表明：

(1)由于需要同時滿足作業軌跡和靶標可視性的約束，因此由DETMAX算法所得測量構型建立的辨識模型仍然相對病態，而采用矩陣平衡法能顯著改善其性態水平。

(2)當測量噪聲增強時，角度DH誤差的辨識偏差依舊維持在0.7%以下，并未產生明顯波動，因此與距離DH誤差相比具有更好的抗噪聲干擾能力。

(3)新方法在2種典型測量噪聲強度下均可滿足機械臂DH參數標定精度要求，因此即使采用普通性能的測量裝備，該方法也具有良好應用潛力。

下一步研究計劃是搭建試驗平臺驗證新方法在現實場景下可行性和標定精度，以此開展實際工況下的優化與完善。其中將重點關注新作業軌跡運行的流暢性以及與四周障礙物間的干涉問題。