懸垂結構零件多軸增材加工非均勻層填充方法
耿聰,耿大鵬,王金杰
(沈陽建筑大學機械工程學院,遼寧沈陽 110168)
0 前言
懸垂結構零件具有底部懸空無支撐的幾何特點,近年來廣泛應用于復雜零件的設計中。增材制造可加工成型任意形狀的零件,是實現復雜形狀零件加工的有效途徑[1-4]。
根據各層厚度是否相同,可將現有算法分為等厚度填充算法和自適應填充算法2類。采用等厚度填充算法所得到的各層厚度相同,算法實現較為簡單[5]。但是,當零件表面曲率變化較大時,使用等厚度填充算法得到的零件表面精度較差。為克服這一不足,自適應填充算法根據零件表面曲率、成型幾何誤差(弦長、體積偏差等)調整各層厚度,得到滿足精度要求的分層[6-9]。
采用三軸混合機床加工懸垂結構零件時,由于加工方向固定,需要添加若干支撐結構[10-11]。這種方式不可避免地會降低整體加工效率,帶來原材料浪費。多軸混合機床在三軸機床結構基礎上增加了旋轉軸,可實現無支撐結構的增材加工。國內外學者對多軸增材加工方法展開了深入研究。ZHANG、LIOU[12]提出了一種適用于多軸增材加工的自適應分層方法,可根據零件表面法向量調整加工方向,實現零件的自適應填充。XIAO、JOSHI[13]開發了一種適用于五軸增材加工的自動規劃軟件,該軟件可自動將零件劃分為多個加工序列進行成型制造。LEE、JEE[14]將零件分解為主體和懸垂部分,在完成主體部分加工后,改變加工方向完成對懸垂部分的加工。上述文獻均將懸垂部分單獨分離,在完成非懸垂部分加工后,再加工懸垂部分,影響整體加工效率。針對這一問題,RUAN等[15]提出將懸垂結構零件作為一個整體進行區域劃分,而后在各個區域采用單層均勻層厚堆疊,最后減材加工形成非均勻層。這種先增材加工而后銑削加工出非均勻層的方法,不僅增加了加工時間,也帶來了材料的浪費。
針對上述問題,本文作者以熔融沉積成型(Fused Deposition Modelling,FDM)為制造工藝,提出一種適用于懸垂結構零件多軸增材加工非均勻層填充算法。與現有方法先增材再減材加工出非均勻層的思路不同,文中方法首先限定階梯誤差最小,確定各層最大層厚、最小層厚和成型角度,進而求解單層填充輪廓,并通過調整增材填充速率,直接形成非均勻厚度層,實現對具有懸垂結構零件的無支撐快速加工,提升整體加工效率。
1 多軸非均勻層成型方法
如圖1所示,懸垂結構零件具有底部懸空無支撐的幾何特點。加工該結構增材時,若原材料成型方向無法改變,則需要構造支撐,影響加工效率和原材料利用率。多軸混合加工機床的刀具在3個平移軸基礎上,增加了旋轉軸,使該類零件的無支撐結構加工成為可能。

圖1 懸垂結構零件示意
文中結合懸垂零件的結構特點,提出適用于懸垂結構零件多軸增材加工非均勻層填充方法。該方法在滿足填充層厚限制的條件下,確定單層兩端層厚d1、d2與成型變化角度θ的變化范圍,在保證填充各層階梯誤差最小的條件下,實現零件的非均勻層填充。算法包括以下4個步驟:(1)讀取模型輪廓數據,建立平面直角坐標系,完成輪廓點坐標由空間直角坐標系到平面坐標系的轉換;(2)在階梯誤差最小的情況下,確定單層兩側層厚和成型變化角度;(3)根據兩側層厚與成型變化角度,確定填充輪廓上各點坐標;(4)通過調整增材填充速率,直接形成非均勻厚度層。下面將分別介紹各部分具體實現過程。
1.1 零件輪廓的確定
如圖2所示,使用三維建模軟件獲取模型數據輪廓s,滿足曲面方程:
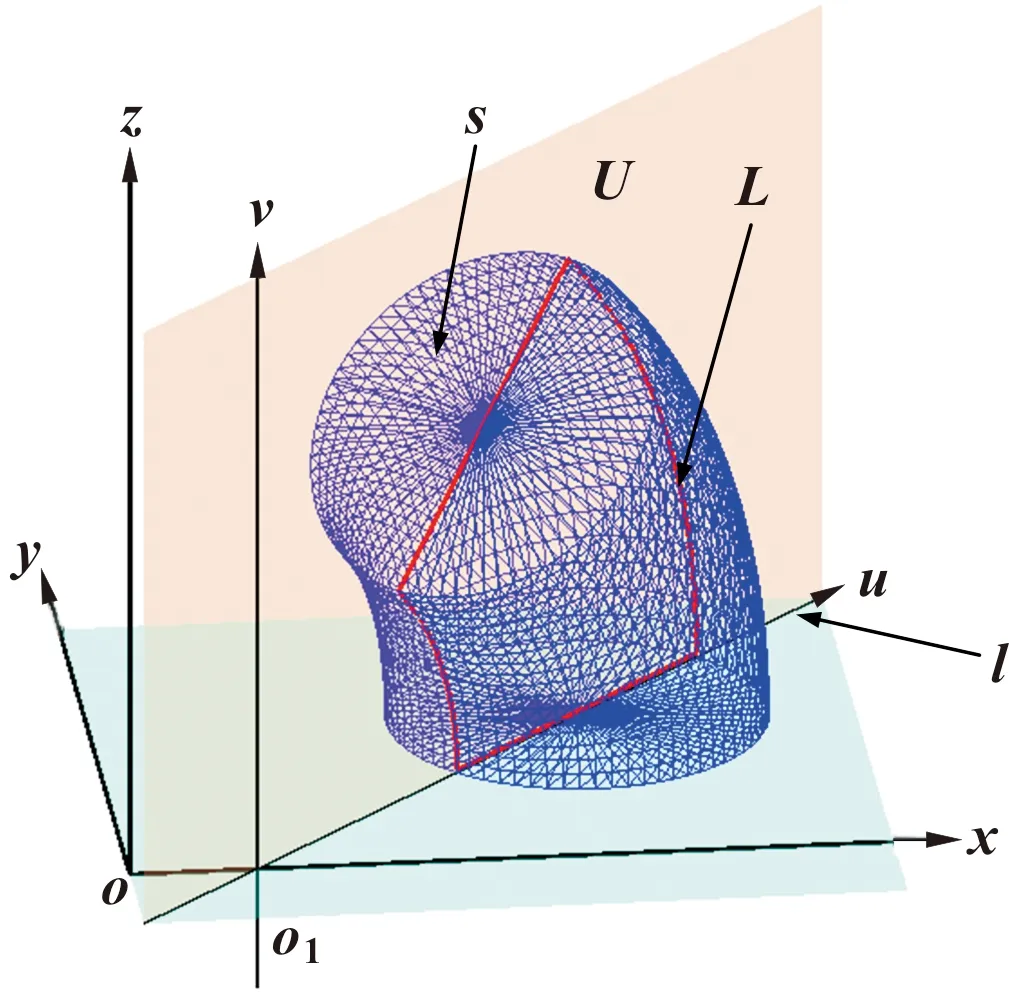
圖2 空間直角坐標系oxyz中的待加工零件
s(x,y,z)=0
(1)
平面U在空間直角坐標系oxyz內垂直平面xy,滿足:
ax+by+c=0
(2)
則零件數據輪廓s與平面U相交所得截面滿足:
z=g(x)
(3)
為使零件數據輪廓s與平面U相交得到的截面輪廓面積L最大,即:
(4)
令其關于自變量a、b、c偏導值為零,可確定平面U的表達式。
(5)
如圖2所示,若平面U與xy平面相交于直線l,該直線與x軸相交于點o1(-c/a,0,0),以點o1為原點,以直線l的單位方向向量為橫軸u,過點o1取與z軸平行的單位向量為v軸,建立右手笛卡爾平面直角坐標系uo1v:
(6)
空間直角坐標系oxyz中任意點P(xp,yp,zp)在所建立的平面直角坐標系uo1v中的點坐標可表示為P(up,vp),滿足:
(7)
1.2 基于最小階梯誤差的多軸非均勻層填充
在建立平面直角坐標系后,零件輪廓點坐標就由空間直角坐標系轉換到平面坐標系中表示。接下來,將在填充階梯誤差最小的前提下,計算單層兩側層厚和成型變化角度,確定各層填充輪廓,并通過調整填充過程中噴嘴的進料速度,實現多軸非均勻層的填充加工。
1.2.1 層厚和成型角度確定
在取得任意零件曲面在平面坐標系中的二維截面輪廓后,此算法采用若干直角梯形近似逼近該截面輪廓。
如圖3所示,連接兩端點A(ua,va)和點B(ub,vb),作AB垂直平分線與BC延長線交于點E(ue,ve),其滿足:

圖3 平面直角坐標系uo1v中對應截面
(8)
如圖4所示,過點E作斜率為ki(i=1,2,…,n)的直線li,與截面輪廓交于點Pi4和Pi6,可將截面分為n層。過直線li-1上的點P(i-1)6作P(i-1)6Pi3垂直直線li于點Pi3,過直線li上的點Pi4作Pi4Pi1垂直直線li-1于點Pi1。點P(i-1)6與點Pi2重合,點P(i-1)4與點Pi5重合,在最底層中,點P(i-1)6與點C重合,點P(i-1)5與點B重合。以此構造出直角梯形Pi1Pi2Pi3Pi4近似逼近各層形狀。在第i層直角梯形中,上底邊Pi2Pi3和下底邊Pi1Pi4的長度分別為該層填充的最小層厚di2和最大層厚di1,上底邊對應的鈍角∠Pi1Pi2Pi3為此層法向量與上一加工平面切向量的夾角。
采用直角梯形層層堆疊形成加工零件輪廓時,加工層與零件在邊緣處存在一定偏差,這種偏差稱為階梯誤差。如圖4所示,當采用實線所示直角梯形Pi1Pi2Pi3Pi4對虛線所示零件第i層進行填充時,由于填充單層層厚較小,該層階梯誤差近似于兩側三角形面積和Si:
Si=SΔPi2Pi3Pi6+SΔPi1Pi4Pi5=
(9)
該輪廓填充的總階梯誤差S表示為各層階梯誤差的總和:
(10)
在滿足層厚限制的條件下,使階梯誤差最小,加工零件各層最小層厚di2、最大層厚di1與成型角度θi的數學模型表示為
其中:dmin、dmax和θmax分別對單層堆疊的最小層厚、最大層厚和最大成型角度;θs為成型總變化角,滿足:
(11)
求解式(11)可確定填充階梯誤差最小條件下各層兩側層厚di2、di1和成型角度θi。
1.2.2 單層填充輪廓的確定
在得到填充階梯誤差最小條件下的各層兩側層厚di2、di1和成型角度θi后,任意層的填充輪廓就可以確定。如圖5所示,任意第i層填充輪廓為由li1、li2、li3、li44條邊組成的直角梯形,Pi2、Pi6、Pi4、Pi5圍成虛線為該層零件截面,∠Pi1Pi2Pi3為直線li1與直線li4相交所成的鈍角,滿足:

圖5 第i層直角梯形逼近截面表示
∠Pi1Pi2Pi3=θi+90°
(12)
在第i層直角梯形中,確定各點坐標Pi1(ui1,vi1)、Pi2(ui2,vi2)、Pi3(ui3,vi3)、Pi4(ui4,vi4)、Pi5(ui5,vi5)和Pi6(ui6,vi6),即可確定該層輪廓。對于底層直角梯形,點P15(B)和點P12(C)為零件輪廓與U軸的2個交點,可通過計算得到;對于其余各層,第i層的Pi2、Pi5分別與i-1層的Pi6、Pi4重合。因此,點Pi2和點Pi5為已知量,只需求解其他4點Pi1、Pi3、Pi4、Pi6。下文將詳細介紹這4點坐標的求解過程。
通過上一步驟確定各層層厚和成型角度后,由于Pi3與Pi2相距di2,且∠Pi1Pi2Pi3已知,可通過式(13)確定Pi3(ui3,vi3):
(13)
直線li2過Pi3(ui3,vi3),且與直線li1垂直,則其表達式為
(14)
確定直線li2表達式后,則可得到跟零件輪廓S相交兩點Pi6和Pi4的坐標值。又由于點Pi1和點Pi4距離是di1,且Pi1Pi4平行于Pi2Pi3,可通過式(15)確定Pi1的坐標值:
(15)
通過上述步驟,可確定第i層直角梯形中所有點坐標,進而確定該層填充輪廓。
1.2.3 填充速率的確定
在增材填充加工過程中,單層填充層厚d滿足:
(16)
其中:r為噴嘴半徑;f為噴嘴進料速度;v為機器移動速度;k為軌跡寬度。對于特定機床,其噴嘴半徑r和軌跡寬度k恒定不變。在實際填充中,保持機器移動速度v不變,單層填充層厚d與噴嘴進料速度f成正比,通過改變噴嘴進料速率即可實現不同層厚的加工。
如圖6所示,增材填充單層時,加工平面由多條填充軌跡組成。每一條填充軌跡的厚度均勻,相鄰填充軌跡的厚度逐步增大,滿足線性關系。路徑加工的截面如圖7所示。

圖6 單層加工面填充軌跡與填充結果
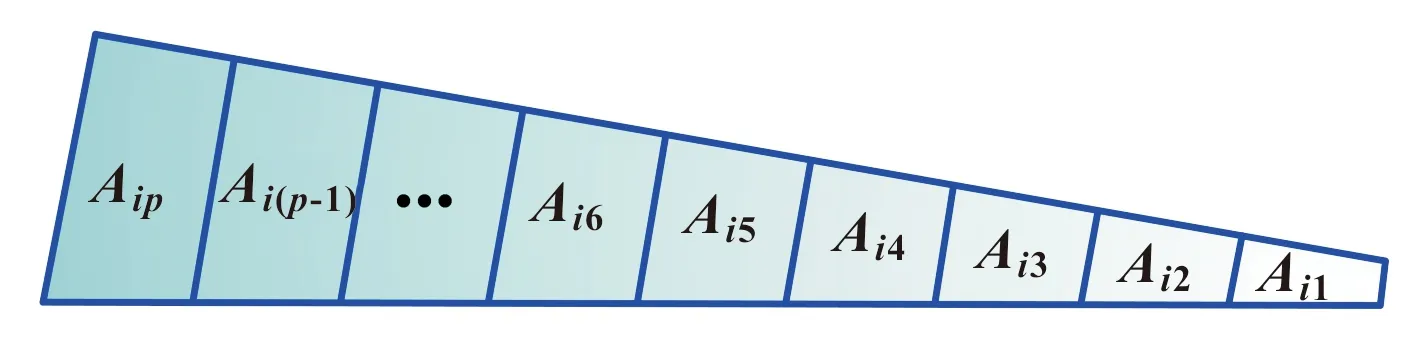
圖7 第i層加工軌跡填充截面
在進行非均勻層填充時,每條軌跡所填充的截面面積Aip可由式(17)確定。
(17)

結合式(16)與式(17),可得出噴嘴在加工軌跡上的進料速率f的表達式:
(18)
2 實驗驗證
為驗證文中所提出算法的有效性,對圖8所示零件進行實驗驗證。該零件是一段半徑為R=45 mm、弧度為π/2的圓弧,其截面為10 mm×10 mm的正方形。設定多軸增材加工機床的噴嘴可填充最小層厚0.5 mm,最大層厚1.0 mm。

圖8 目標加工零件
圖9所示為等厚度填充仿真效果。圖10所示是根據曲率變化對零件進行自適應填充的仿真效果,可以看出:各層厚度在0.5~1.0 mm內變化。與等厚度填充法相比,自適應填充算法得到的各層厚度不同,但兩方法在填充單層時的厚度均保持不變。圖11所示為采用文中方法對零件進行非均勻填充的仿真效果。圖中相同顏色部分的堆疊厚度相同,同層填充厚度在0.5~0.625 mm內變化。與等厚度和自適應填充方法不同,采用文中方法填充,單層厚度也會發生變化。
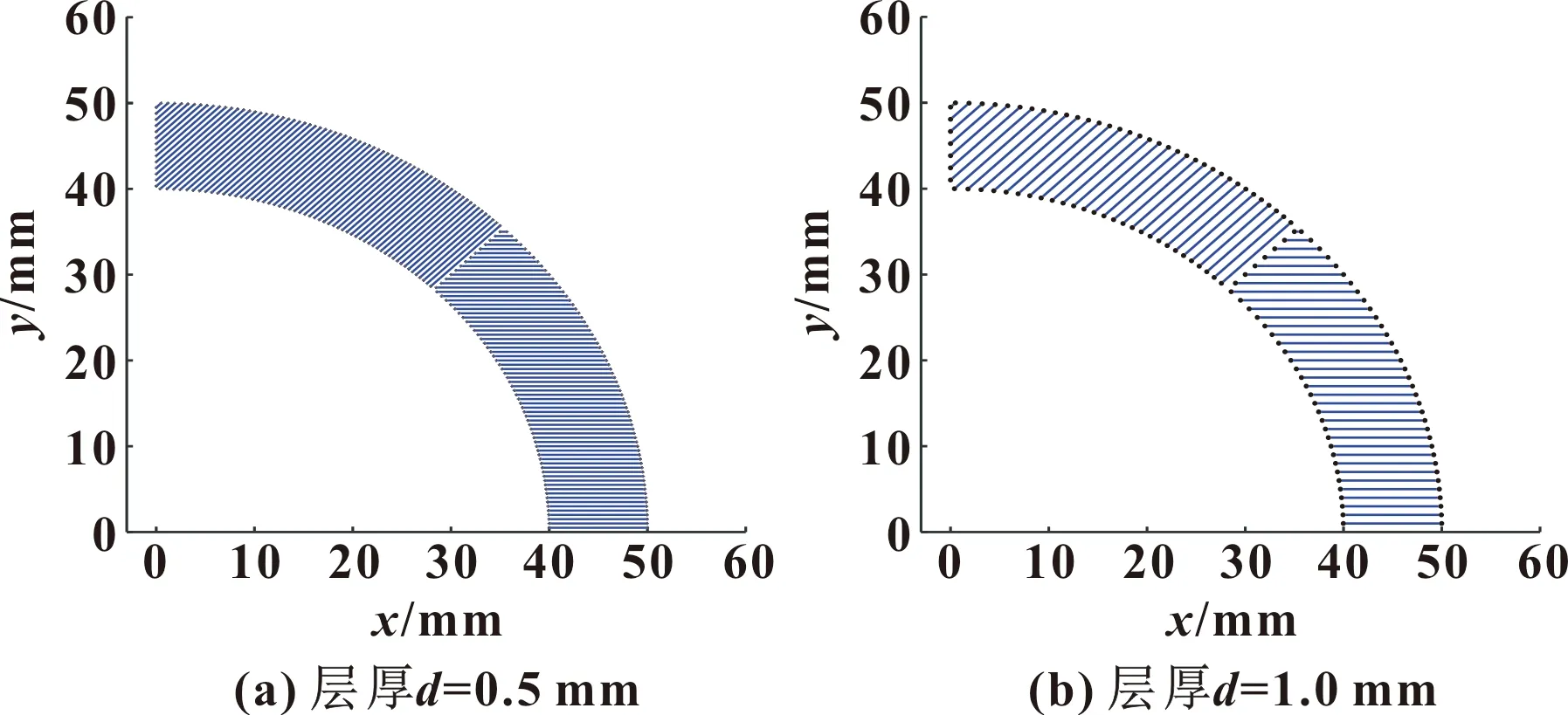
圖9 等厚度算法分層仿真結果
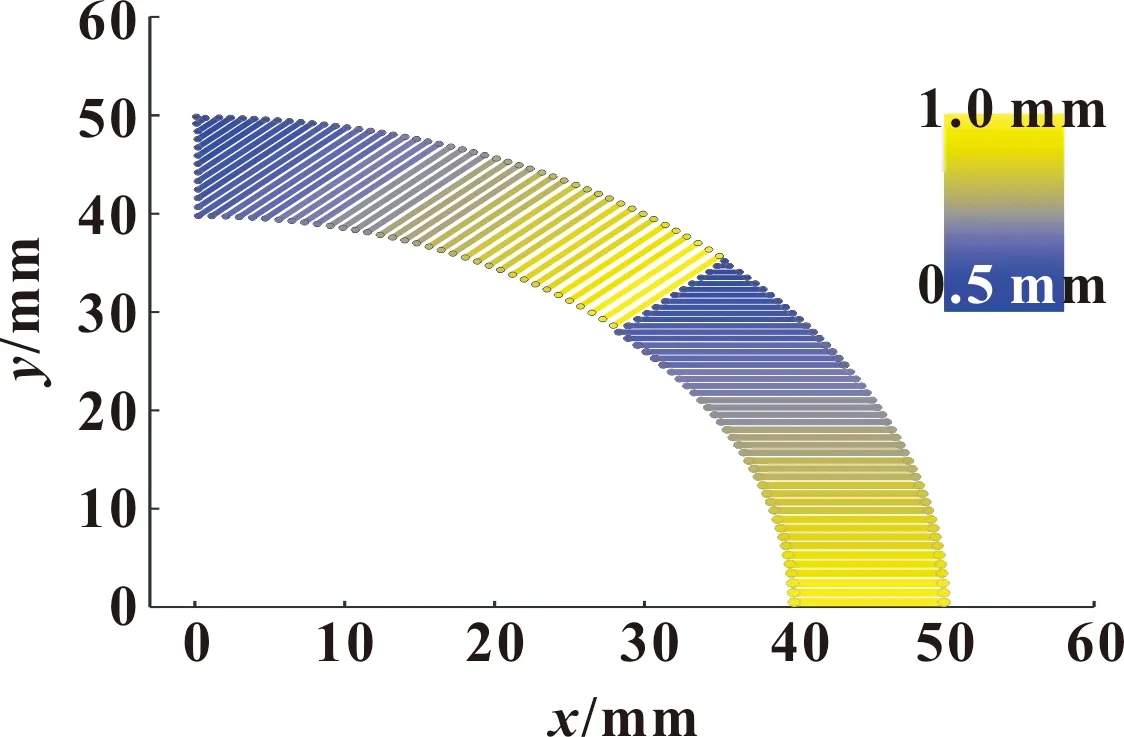
圖10 自適應算法分層仿真結果

圖11 文中方法分層仿真結果
效率和精度是評價算法效果的兩個重要指標,兩者與填充層數和填充層階梯誤差的大小有關,層數越多,效率越低,各層階梯誤差越小,增材填充精度越高。表1所示為分別采用等厚度填充算法、自適應填充算法和此算法對圖8所示零件加工,在層數、填充面積與階梯誤差間的差異。可知:在滿足噴嘴最大加工層厚的情況下,文中方法與等厚度填充算法得到的層數分別為79和70,遠小于自適應填充算法得到的層數92。

表1 不同分層方式參數與實驗數據對比
設定機床的噴嘴可填充最小層厚0.5 mm,最大層厚1.0 mm,在得到分層信息后,采用Vericut中的beam_magic2機床進行仿真加工,噴嘴加工寬度為1 mm,移動速度為80 mm/s,增材仿真加工的結果如圖12所示。
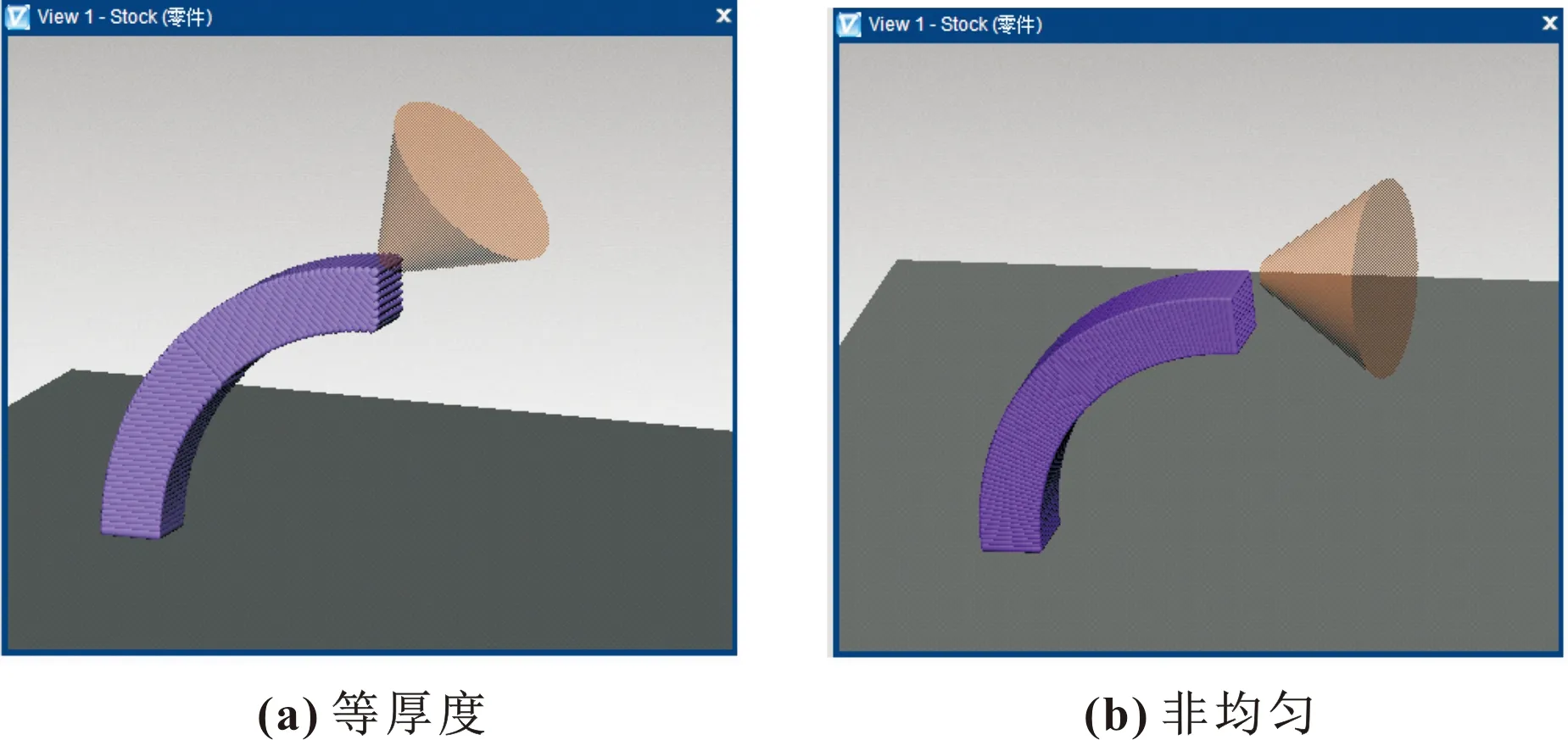
圖12 零件填充加工
在增材填充過程中,層數與效率成反比,層數越多,待填充加工面積越大,其效率越低,加工數據如表1所示。采用文中方法加工,其填充面積為7 900 mm2,與等厚度填充算法面積(6 969 mm2)相近,遠小于采用自適應填充算法進行填充的加工面積(9 086 mm2)。這意味著在該零件的加工中,采用文中方法和等厚度填充算法能夠得到較高的加工效率。
采用等厚度填充算法對該零件進行實驗加工時,形成的階梯誤差為7.206 1 mm2,遠大于文中方法填充階梯誤差0.647 9 mm2。為提升等厚度填充算法加工精度,一般采用增加等厚度填充層數的方法。在將分層層數增至140,加工層厚限定至最小值0.5 mm后,填充階梯誤差由7.206 1 mm2縮小到3.632 1 mm2,但填充面積由6 969 mm2增至14 036 mm2,大大降低了加工效率。而當文中算法加工層厚取最小值時,誤差可達到最小值0.252 3 mm2,不僅優于等厚度填充算法和自適應填充算法,而且還優于文中加工層厚取最大值時的誤差。文中加工層厚取最小值時,填充面積由7 900 mm2增至12 600 mm2,會降低加工效率、提高加工精度。
采用文中方法進行實際加工,填充加工材料為PLA,加工出的零件如圖13所示。

圖13 加工零件
綜上所述,相較于等厚度填充、自適應填充等均勻層厚填充方法,在滿足填充層厚的條件下,采用文中方法對零件進行加工,可獲得更好的加工效率和加工精度。
3 結論
文中提出一種針對具有懸垂特征零件的多軸增材加工非均勻層填充算法。該方法將模型輪廓三維點坐標轉換為平面直角坐標系中的二維點表示,在保證階梯誤差最小的情況下,確定各層兩側層厚和堆疊角度,進而得到填充輪廓上各點坐標。實驗結果表明:與傳統等厚度填充和自適應填充方法相比,文中方法采用一系列非均勻層完成零件的填充加工,該過程無需支撐結構,且與傳統均勻層填充方法相比,文中方法能夠達到更高的加工效率與加工精度。文中方法同樣適用于曲率變化大零件的增材填充。

