找準“著力點”巧解立體幾何解答計算題
——2023年高考數學立體幾何解答題第二問破解啟示

西藏民族大學附屬中學(712082) 袁義東

西藏自治區教育考試院(850000) 呂呈蘢

2023 年高考數學試題以落實立德樹人根本任務,促進學生德智體美勞全面發展,反映新時代基礎教育課程理念,落實考試評價改革等相關要求精彩亮相. 立體幾何試題著力基礎,彰顯能力,突出創新與應用,極好地發揮數學學科在人才選拔中的重要作用. 現以2023 年高考數學全國甲卷文理卷,乙卷文理卷,新課標I 卷,II 卷立體幾何解答題第二問題型破解、感悟高考數學的靈活性和創新性, 啟示新課標, 新高考,新教材情境下中學數學教育教學的有效開展.

一、題型解析

1. 求幾何體的高

題目1(2023 年高考甲卷文科第18 題(2))如圖,在三棱柱ABC-A1B1C1中,A1C⊥平面ABC,∠ACB=90?.

(1)證明: 平面ACC1A1⊥平面BB1C1C;

(2)設AB=A1B,AA1= 2,求四棱錐A1-BB1C1C的高.

解析(1)略.

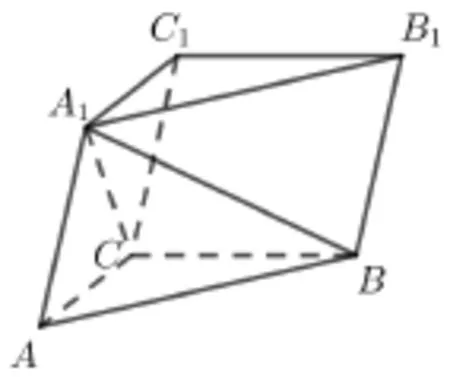
圖1

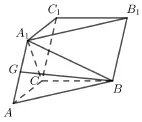
圖2

(2)取G為AA1的中點,連接CG,BG,由題知ACC1A1為平行四邊形, 所以C到AA1的距離和A1到CC1的距離相等, 由(1) 知平面ACC1A1⊥平面BB1C1C;A1到平面BB1C1C的距離即A1到交線CC1的距離, 因為AB=A1B, 所以GB⊥AA1; 由(1) 可知,BC⊥平面ACC1A1,AA1?平面ACC1A1, 所以BC⊥AA1; 又BC ∩BG=B, 所以AA1⊥平面BCG, 因為CG ?平面BCG, 所以CG⊥AA1; 因為AB=A1B,AA1= 2, 且A1C⊥平面ABC,從而AC=A1C,所以AC=所以CG= 1. 故A1到平面BB1C1C的距離為1, 所以四棱錐A1-BB1C1C的高為1.

啟示突破第二問的關鍵是將四棱錐A1-BB1C1C的高轉化為A1到平面BB1C1C的距離,借助面面垂直的性質定理,進而將問題轉化為A1到交線CC1的距離,利用平面ACC1A1為平行四邊形,順利求解. 這啟示我們;平時教學要時時刻刻注意數學思想方法的運用,對空間計算要力爭轉化為平面計算,降低運算的難度.

2. 求幾何體的體積

題目(2023 年高考乙卷文科第19 題(2))如圖,在三棱錐的中點分別為D,E,O, 點F在AC上,BF⊥AO.

(1)證明:EF//平面ADO;

(2)若∠POF=120?,求三棱錐P -ABC的體積.

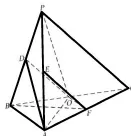
圖3

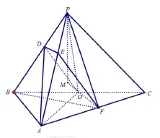
圖4

解析過P作PM垂直FO的延長線交于點M,因為PB=PC,O是BC中點,所以PO⊥BC. 在Rt?PBO中,所以

因為AB⊥BC,OF//AB,所以OF⊥BC,又PO ∩OF=O,PO,OF ?平面POF,所以BC⊥平面POF、又PM ?平面POF, 所以BC⊥PM, 又BC ∩FM=O.BC,FM ?平面ABC,所以PM⊥平面ABC,即三棱錐P -ABC的高為PM,因為∠POF=120?,所以∠POM=60?,所以

啟示突破第二問的關鍵是在確立F是中點的基礎上,進一步確立BC⊥平面POF從而P點在平面ABC的投影落在OF的延長線上就成為解決這一問題的突破口,因為∠POF=120?,所以∠POM=60?,進而獲得高,求得體積.這也啟示我們數學教學培養學生的空間意識,讓學生在解題中感悟空間結構和條件轉化.

3. 求線面夾角的正弦值

題目3(2023 年高考甲卷理科第18 題(2))如圖,在三棱柱ABC -A1B1C1中,A1C⊥平面ABC,∠ACB=90?,AA1=2,A1到平面BCC1B1的距離為1.

(1)證明:A1C=AC;

(2) 已知AA1與BB1的距離為2, 求AB1與平面BCC1B1所成角的正弦值.

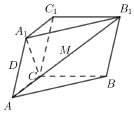
圖5

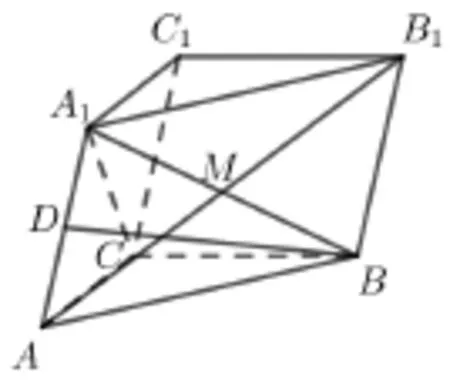
圖6

解析因為AC=A1C1,BC⊥A1C,BC⊥AC, 故Rt?ACB∽= Rt?A1CB. 因為BA=BA1過B作BD ⊥AA1,交AA1于D,則D為AA1中點,與BB1距離為2,所以BD= 2,因為A1D= 1,BD= 2,因為在Rt?ABC, 因為BC=延長AC,使AC=CM,連接C1M,由CM//A1C1,CM=A1C1知四邊形A1CMC1為平行四邊形, 因為C1M ⊥AM, 從而C1M ⊥平面ABC,又AM ?平面ABC,因為C1M ⊥AM,則在Rt?AC1M中,AM= 2AC,C1M=A1C, 因為中,

因為

又A到平面BCC1B1距離也為1, 所以AB1與平面BCC1B1所成角的正弦值為

啟示由于A到平面BCC1B1距離也為1,所以AB1與平面BCC1B1所成角的正弦值的突破口就是求AB1的長. 由A1C ⊥平面ABC為我們提供了面面垂直, 將AB1放置在平行四邊形A1CMC1中,創建直角三角形,從而得出結論. 這里用的是數形結合的“形化數”;啟示我們在數學教學時,要找準“著力點”,靈活運用推理與運算進行計算.

4. 求二面角的正弦值

題目4(2023 年高考新課標II 卷第20 題(2) ) 如圖, 三棱錐A - BCD中,DA=DB=DC,BD⊥CD,∠ADB=∠ADC=60?,E為BC的中點.

(1)證明:BC⊥DA;

(2)點F滿足求二面角D-AB-F的正弦值.

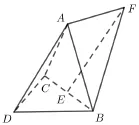
圖7

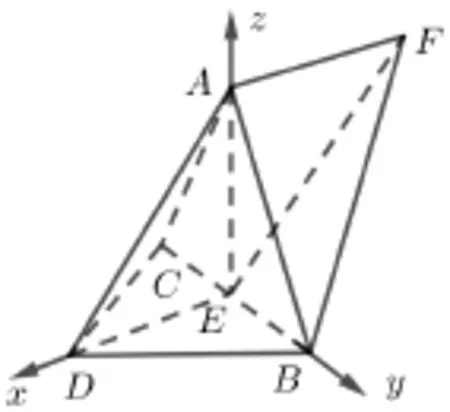
圖8

解析設DA=DB=DC=2,所以BC=因為所以AE2+DE2=4=AD2,所以AE⊥DE,又因為BC⊥AE,DE ∩BC=E,所以AE⊥平面BCD, 以E為原點, 建立如圖所示空間直角坐標系,設平面DAB與平面ABF的一個法向量分別為n1= (x1,y1,z1),n2=(x2,y2,z2),則

令x1=1,解得y1=z1=1;令y2=1,解得x2=0,z2=1,故n1= (1,1,1),n2= (0,1,1),設二面角D-AB -F的平面角為θ, 則故所以二面角D-AB-F的正弦值為

啟示解決這一問題的關鍵就是合理建立坐標系,進而證明AE⊥平面BCD就是解決問題的突破口,之后就是用向量法求二面角的常規做法,試題選擇求二面角D-AB-F的正弦值的主要好處在于: (1)答案確定;(2)避免了二面角為非特殊值的麻煩;(3)若選擇余弦值就有可能取正負,增加了答案的不確定性. 其中2023 年全國乙卷理科的立幾題目的第3 問也是求二面角的正弦值,這正是命題的高明之處.

5. 利用二面角求值

題目5(2023 年高考新課標I 卷第18 題(2))如圖,在正四棱柱ABCD-A1B1C1D1中,AB= 2,AA1=4. 點A2,B2,C2,D2分別在棱AA1,BB1,CC1,DD1上,AA2= 1,BB2=DD2=2,CC2=3.

(1)證明:B2C2//A2D2;

(2)點P在棱BB1上,當二面角P-A2C2-D2為150?時,求B2P.

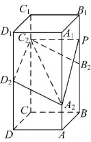
圖9

圖10

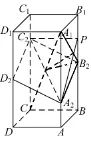
圖11

解法1以C為坐標原點,CD,CB,CC1所在直線為x,y,z軸建立, 空間直角坐標系, 如圖, 則C(0,0,0),C2(0,0,3),B2(0,2,2),D2(2,0,2),A2(2,2,1),所以又B2C2,A2D2不在同一條直線上, 所以B2C2//A2D2. 設P(0,2,λ)(0 ≤λ≤4), 則設平面PA2C2的法向量n=(x,y,z),則

令z=2,得y=3-λ,x=λ-1,所以n=(λ-1,3-λ,2).

設平面A2C2D2的法向量m=(a,b,c),則

令a=1,得b=1,c=2,所以m=(1,1,2),所以

化簡可得,λ2-4λ+ 3 = 0, 解得λ= 1 或λ= 3, 所以P(0,2,1)或P(0,2,3),所以B2P=1.

解法2聯結A1C, 交A2C2于點O, 聯結A1B2, 交PA2于點M, 聯結OM. 由題意所以由題意A2B2=所以A2C2⊥B2O, 又因為A1O ∩B2O=O,故A2C2⊥面A1OB2, 又因為OM ?面A1OB2, 所以A2C2⊥OM, 所以∠MOB2為二面角P - A2C2- B2的平面角, 即∠MOB2= 30?,Rt?A1B2O中故∠OB2A1= 60?, 所以∠OMB2= 90?, 故因為從而PB2=1.

啟示解法1 通過建立坐標系,用坐標建構二面角關系,重點在于對公式的熟悉程度和運算;解法2 用幾何法建構二面角關系,重點是二面角的平面角在圖形中體現,二面角的合理使用就是解決問題的突破口.

二、教學建議

從2023 年高考數學立體幾何解答題第二問的解析不難看出,新高考試題在充分彰顯試題的一核四層四翼,把能力和素養考查建立在基礎知識掌握和基本技能運用上,從考題破解給我們以下教學建議:

1. 立體幾何解答題以幾何體為載體,以點線面為著力點,以幾何建構和坐標系搭建為突破口,建立平面幾何數量關系,實現試題的解答計算.

2. 立體幾何計算題的基本類型: 長度、面積、體積的計算;線線、線面、面面的夾角計算;線線、線面、面面的夾角三角函數值計算;這些知識都能較好的考察學生的空間想象能力和運算能力等學科素養.

3. 從2023 年高考立體幾何解答題第二問題型考查上看,全國卷重點考察了其中的5 類,尤其是二面角的正弦值的計算,彰顯了高考試題的有利性和確定性,啟示我們數學教學重視基本訓練,強化基本能力,認真踐行核心素養.

4. 面對新高考,新課標,新教材,教學時一定要做到以學生為主體,以教師為主導,面對建立在空間幾何體的基礎上立體幾何的計算題,找準“著力點”,合理搭建圖形關系,理順解題思路,以新的教學方式適應新高考的要求.

總之,2023 年高考數學試題精彩多多,亮點多多,給我們的啟示頗多. 發展素質教育,當好學生“引路人”,從真正意義上踐行教書育人的教育準則,把立德樹人,為黨育人,為國育才貫穿于教育的每一步;通過立體幾何解答題第二問的破解讓我們感悟到找準“著力點”是巧妙突破解答計算的關鍵;也再次啟示我們在新課標,新教材,新教法的實施中,從知識的內涵與外延入手,抓好思維訓練,培養學生探究能力和創新意識,積極踐行核心素養,有力推動新型人才培養!