滲透轉化思想　助力學生深度學習“圖形與幾何”

摘 要：數學的深度學習在于數學思想的深入。有了數學思想的支撐，學生會知其然且知其所以然，深刻地理解數學內容，掌握數學學習方法，靈活地解決數學問題，發展數學學科核心素養。轉化思想是數學思想方法之一。為了使學生深度學習“圖形與幾何”內容，教師要滲透轉化思想，深入研讀教材、精選教學方法、積極實踐操作。

關鍵詞：小學數學；轉化思想；“圖形與幾何”；滲透策略

中圖分類號：G427? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼：A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文章編號：2097-1737（2023）25-0080-03

常用的數學思想有很多，轉化思想是最基本、最常用的一種思想，在小學數學教學中有著廣泛的應用價值。小學數學“圖形與幾何”中蘊含轉化思想的內容較為豐富，如“多邊形的面積”“立體圖形的面積”“立體圖形的體積”[1]。在“圖形與幾何”教學中滲透轉化思想，可以使學生獲得解決數學問題的有效途徑。

一、深入研讀教材，挖掘轉化思想

數學教材是數學知識的載體，教師要深入研讀教材中的“圖形與幾何”內容，分析知識領域間的知識結構、作用，探尋具體知識背后的合適方法，挖掘轉化思想，夯實課堂教學基礎。

例如，圓的面積以長方形的面積為基礎。在學習圓的面積時，學生需要轉化已有的知識經驗，將未知面積公式的平面圖形轉化為已知面積公式的平面圖形。簡單地說，學生要平均分圓，拼成一個近似于長方形的圖形。接著，學生要對比圓和這個近似于長方形的圖形，發現二者之間的聯系，然后遷移已有認知，回想長方形的面積公式，列出算式并化簡，得出圓的面積公式。通過探尋知識背后的合適方法，教師挖掘出了轉化思想，引導學生體驗數學操作活動，經歷轉化過程，借此實現知識間的融會貫通，扎實掌握轉化思想與方法，發展幾何直觀素養，實現深度學習。

二、精選教學方法，融入轉化思想

“圖形與幾何”中的大部分內容具有抽象性，對于大部分小學生而言存在較大的理解難度。應用轉化思想，可以在一定程度上降低“圖形與幾何”內容的抽象性，助力學生直觀化、形象化、具體化地探究數學內容，建立深刻的認知[2]。

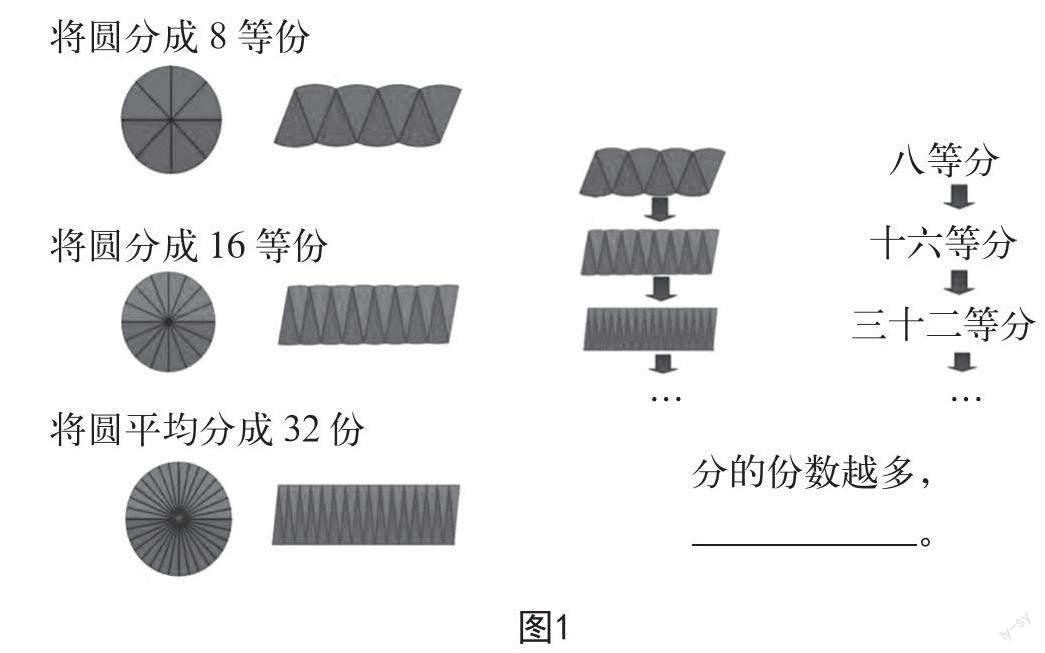
例如，“圓的面積”這節課的教學重點是讓學生將圓平均分為32份或64份，拼接、轉化為一個近似于長方形的圖形。將圓平均分為32份或64份，對于大部分學生而言有一定困難。針對此情況，在教學“圓的面積”之前，教師以轉化圓為近似于長方形的過程為重點，錄制微課，動態展現轉化過程。在課堂上，教師先引導學生回顧平行四邊形、三角形的面積推導過程，總結方法。大部分學生遷移已有認知，在腦海中浮現不同的推導過程，發現相似之處，總結出具體方法——經過剪切、拼接，將未知面積公式的圖形轉化為已知面積公式的圖形。之后，教師鼓勵學生發揮想象力，設想“可以將圓剪切、拼接為什么圖形？”學生發散思維，積極聯想，提出不同的猜想及操作方法。大部分學生提道：“可以將圓平均分成不同的份數，剪切、拼接，得出一個新圖形。”教師對學生進行贊賞，并借助電子白板播放微課。在觀看微課時，學生發現“隨著平均分的份數越多，拼出的圖形越來越像長方形”（如圖1）。

于是，教師鼓勵學生對比圓和近似長方形的圖形，分析、總結二者之間的關系。在此過程中，大部分學生遷移已有認知，對比圓的周長、半徑與近似長方形圖形的長、寬，直觀地發現二者之間的關系。無須教師引導，學生主動回想、書寫長方形的面積公式，并應用發現的關系，延展公式、簡化公式，得到圓的面積公式。教師依據學生的學習情況，總結具體方法和數學思想。之后，教師鼓勵學生設想其他方法，將圓轉化為其他熟悉的圖形，繼續探究圓的面積公式。

三、積極實踐操作，應用轉化思想

（一）在知識生成中應用轉化思想

學生探究知識的方式有很多，實踐操作是其中之一。實際上，實踐操作的過程正是學生親歷轉化的過程。在此過程中，學生會積極思考，遷移已有認知，透過數學現象發現結論，扎實掌握數學知識，獲取轉化思想，發展形象思維能力、歸納總結能力。

例如，在教學“圓的周長”時，教師先引導學生探究圓的周長的內涵。在探究后，大部分學生認識到“圍成圓的曲線的長是圓的周長”。基于此，教師鼓勵學生探究圓周長計算方法。在探究時，學生主動與其他小組成員交流。部分小組成員遷移已有認知，聯想有關方法并主動分享。如有的組員提出：“可以用繩子繞著圓套一圈，繩子的長度就是圓的周長。”在此提議下，小組成員動手操作，并測量繩子的長度，記錄數據。之后，小組成員觀察、比較繩子的長度和圓的直徑，發現繩子長度是圓的直徑的3倍多一點。面對如此發現，

小組成員繼續選擇不同大小的圓，使用繞繩法進行測量，獲得數據，認真計算。最后，小組成員綜合比較計算結果，得出結論：圓的周長是直徑的3倍多一些。

在實踐操作后，該小組毛遂自薦，展示操作過程和結果。其他小組在觀看、傾聽時，結合本組的實踐操作成果，提出其他方法。最終，全體學生依據操作結果，達成共識：圓的周長是直徑的3倍多一些。

在不知道圓的周長計算公式的情況下，學生動手操作，將未知的曲線（圓的周長）轉化為可以度量的線段，利用已有知識探究、得到新知識，實現了有意義建構，切實地拓展了學習深度。

（二）在解決問題中應用轉化思想

轉化思想是學生解決問題的“工具”。尤其，學生掌握轉化思想不是一件一蹴而就的事情，需要經過反復訓練。教師要依據學生的數學學習情況，組織問題解決活動，促使學生應用轉化思想解決數學問題，建構數學認知，內化轉化思想，增強深度學習效果。

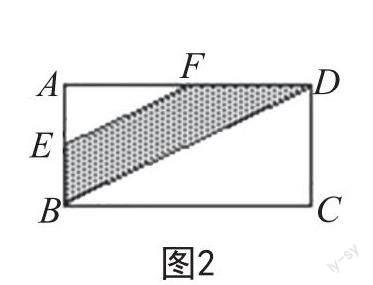
例如，在教學“多邊形的面積”后，教師組織問題解決活動——求復雜圖形的面積。在活動中，教師呈現題目：如圖2所示，ABCD是一個長方形，長12 cm，寬6 cm。E、F分別是AB、AD的中點。請問陰影部分的面積是多少？

教師鼓勵學生合作解決問題。在合作的過程中，大部分學生邊觀察圖像邊動腦，發揮空間想象能力，依據問題條件，梳理思路，繼而動手操作，解決問題。

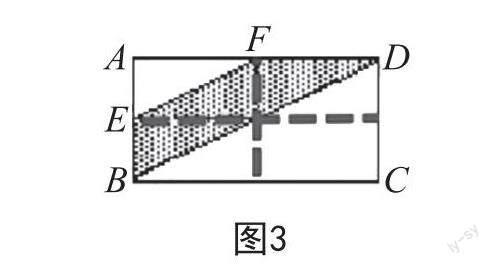
有小組代表提出：“從E點出發，向對邊作一條垂直線段；從F點出發，也向對邊作一條垂直線段，此時得到四個大小相同的小長方形。”依據小組代表的思路，教師操作電子白板，展示相關內容（如圖3）。

小組代表據此繼續介紹：“經過如此操作，陰影部分變成了三個大小相同的小三角形。”其他學生在傾聽時主動發問：“怎樣確定這三個小三角形大小一樣？”小組代表對照圖像，分析三個三角形的底和高的長度，給出“等底同高”的結論。接著，小組代表依據三角形的面積公式列出算式，得出所求陰影部分的面積。

在這個過程中，其他學生提出不同的看法。如“如此分割后，陰影部分是一個平行四邊形和一個直角三角形。平行四邊形的底是6 cm，高是3 cm，三角形的兩條直角邊分別是6 cm和3 cm，根據平行四邊形、三角形的面積公式，列出算式：6×3+6×3÷2=27 cm2。”

在問題解決的過程中，學生發揮空間想象能力，遷移已有數學認知，鞏固了所學知識，運用了轉化思想。教師把握時機，繼續呈現類似的問題，驅動學生繼續解決。通過不斷解決問題，學生扎實掌握了轉化思想，培養了空間觀念、幾何觀念和數學運算能力。

四、結束語

總之，有效滲透轉化思想，便于學生深度學習“圖形與幾何”的內容，建構知識體系，發展核心素養，增強學習效果。對此，在實施小學數學“圖形與幾何”教學時，教師可以依據“圖形與幾何”教學內容，挖掘轉化思想，選用適宜的方式，促使學生體驗知識生成活動和問題解決活動。在體驗活動時，學生會積極思維，遷移已有認知，想象、操作，掌握數學知識，建構知識體系，同時發展數學學科核心素養。

參考文獻

柏煜.探討小學高年級數學教學中轉化思想的滲透與運用[J].才智，2020（14）：98.

陳兆勇.基于深度學習的小學數學圖形與幾何教學探析[J].福建教育學院學報，2020，21（3）：77-78.

作者簡介：黎美薇（1981.5-），女，廣東廣州人，任教于廣州市海珠區實驗小學，一級教師，本科學歷，廣州市骨干教師，執教的課例曾兩次在“一師一優課，一課一名師”活動中被評為部級優課。