學教評一致性背景下的“平行四邊形的面積”教學實踐與思考
劉業生

一、問題的提出
“平行四邊形的面積”一課是一節小學數學經典課例,不同版本的內容編排也基本相同,基本都包括數方格法比較面積、公式猜想、推導公式等環節。由于該課的可操作性強,該內容經常亮相各大賽課平臺。筆者在系統接受學教評一致性理論知識后,在學教評一致性背景下重新思考該節課例,“平行四邊形的面積”一課承載了哪些數學核心素養?最核心的素養是什么?這些核心素養該如何在教學之中體現?這節課的最核心目標是什么?“數方格”的教學價值又體現在哪里?如何剪拼?基于以上思考,筆者開展了相關的行動研究和課例研究,聚焦面積這一本質內容,促進“量感”這一核心素養培育。
二、學教評一致性背景下的核心素養和核心目標的確定
(一)核心素養的確定
通過研究課標和不同版本教材分析,我們認為“量感”是本節課的核心素養,我們認為公式猜想就應該回歸到圖形面積概念本質,從“數方格”即“數面積單位”的角度去提出猜想,緊扣面積本質屬性,不但數整格的面積單位,還讓學生在將兩個半格合成一格的思量中感受到接下來為什么要進行圖形的轉化,很好地促進量感教學的同時,感受到數學“轉化法”的重要性。
(二)核心目標的確定
1.經歷數方格求平行四邊形面積的過程,體會面積的本質——面積單位的疊加,初步滲透圖形轉化思想,建立量感。2.通過操作、探究、對比、交流,經歷平行四邊形面積的推導過程,初步體會數學轉化的思想,發展學生的推理意識。3.掌握平行四邊形面積公式的計算方法,能在現實中解決實際問題,促進數學學習的應用意識。
三、學教評一致性背景下的“平行四邊形的面積”教學實踐
(一)情境激趣,引發猜想
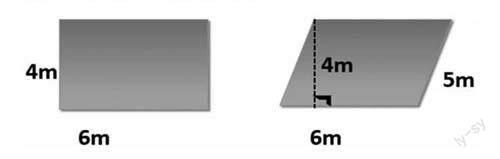
教師播放微課,出示地主分地的故事:從前有個地主,他給兩個兒子分地,給大兒子分了一塊長方形的地,給小兒子分了一塊平行四邊形的地,可是兩個兒子都認為分給自己的那塊地小,都說老地主偏心。(如下圖)在學生讀懂數學信息后,教師拋出問題:你們認為哪塊地的面積大呢?學生根據教師提供的沒有標數據的兩個圖形,運用所學知識大膽進行猜測。在猜測中感覺到要計算出兩塊地的面積,需要給出相關數據,為了便于研究,教師提供兩個圖形(如下圖)的相關數據,在學生計算完左邊長方形的面積后,教師引導學生大膽猜測平行四邊形的面積會該怎么求?
學生匯報,教師記錄下學生的三種猜想:6×4=24 m2????? 6×5=30 m2
5×4=20 m2 。
師生明確三種猜想所對應的公式分別為:平行四邊形的面積=底×高,平行四邊形的面積=鄰邊×鄰邊,平行四邊形的面積=底×不對應的高。但哪種算法才是正確的?學生爭論不一。
師:到底哪種猜想是對的呢?教師揭示課題:平行四邊形的面積。
思考:新課標中“推理意識”核心素養明確要求:能夠通過簡單的歸納或類比,猜想或發現一些初步的結論。本節課通過地主分地創設比較平行四邊形和長方形面積大小的需要,通過情景激趣,引發對平行四邊形面積公式的三種猜想,從而進一步激發學生運用不同方法去驗證猜想的學習興趣。
(二)動手操作,驗證猜想
1.直觀度量,初步驗證。教師提供方格情境,供學生探索。
在方格紙上數一數,然后填寫下表。(一個方格代表1 m2)
在學生動手操作之前,師引導生一起弄清楚每個方格代表1平方米的具體含義。
生動手數方格,并完成學習單上的學習任務。師組織學生分享結果,平行四邊形的面積數方格得出來的結果為24格,面積為24平方米。教師及時追問:“大家在數的時候,有沒有什么小竅門?”,通過問題引領,引導學生發現數的時候可以將左邊的角部分移到右邊就會變成學過的長方形,數起來更方便。
師:這種方法在數學上稱為“割補法”,也是一種轉化的方法,引出課題:平行四邊形的面積。
教師通過繼續追問:“通過對比左右兩個圖形的數據,你有什么發現?”在思維碰撞中學生發現兩個圖形的面積是相等的,還有學生初步發現了平行四邊形的底與高分別與長方形的長和寬是相等的。學生從數據上的觀察初步認為平行四邊形的面積應該是底乘高。師進一步追問:“是不是所有的平行四邊形的面積都等于底乘高呢?”接下來開始第二個驗證。
2.轉化推理,再次驗證。師出示第二個驗證任務,并引導學生明確任務一:選擇一個平行四邊形將它轉化為長方形。學生利用課前教師發下的4個不同形狀的平行四邊形學具,小組合作,動手操作。在核心問題“可以從什么地方剪?”的驅動下,各組開展動手操作,2組學生代表主動上臺匯報,2組學生分別采用的都是沿平行四邊形最邊上的高剪開通過平移拼成長方形。在學生進一步思辨下,師生明確還可以沿中間的高剪拼成長方形的情況。
3.深入理解,歸納小結。師出示任務二:觀察剪拼的圖形,長方形的長和寬與平行四邊形的底和高有什么關系,由長方形的面積公式如何推導出平行四邊形面積公式?生自由討論,繼續完成學習單上相應任務后,在核心問題“該如何剪?為什么這樣剪?”的引領下,教師組織匯報,在操作和觀察后,學生進一步發現長方形的長與平行四邊形的底相等,長方形的寬與平行四邊形的高相等這組關系,同時根據長方形的面積公式得出平行四邊形的面積等于底乘高。在核心內容的驅動下,學生對于課前三種猜想中的第一種猜想:平行四邊形的面積=底×高有了進一步的理解。
(三)學以致用,總結反思
為了避免學生只注重對公式的機械運用,在練習環節設計了如下的梯度訓練題:第一層次:前后呼應:“現在可以知道兩個兒子誰分的地大了嗎?”第二層次:聯系生活實際,計算車位的面積,給出平行四邊形兩組底和高。第三層次:選一選,給出三組數據—給出鄰邊的長度、一組對應的底和高,讓學生選擇正確的計算算式。并利用微課解釋為什么平行四邊形面積不能鄰邊×鄰邊。在最后全課小結后,教師布置了一道思考銜接題:“分到平行四邊形地的小兒子決定將這塊地平均分成兩個三角形地,一塊地用來種龍眼樹,一塊地用來種荔枝樹,你知道它們的面積各是多少嗎?”為接下來的三角形面積的教學做好鋪墊。
四、思考與結論
(一)明確水平層次及學習路徑,構建知識間的聯系
教師在教學這節課時,要引導學生充分利用已有的圖形與幾何的學習經驗進行自主探索,在不斷操作和對比聯系已學知識基礎上逐步推導出平行四邊形的面積公式。我們確定本節課通過讓學生經歷猜想、驗證這兩大環節,從故事地主分地入手,引發學生對平行四邊形面積計算公式的猜想,然后讓學生經歷方格圖數一數以及沿高剪拼的兩大核心任務,以學生作品為基礎,溝通了平行四邊形與長方形之間的聯系,驗證并確定了平行四邊形面積計算公式,最后再進行鞏固練習,明確學習路徑,能更好地建構知識之間的關聯,更好地實現“結構地教,關聯地學”。
(二)核心任務驅動,有效提高課堂教學實效
在設計核心任務時,我們重點基于以下幾個思考:學生怎么會自覺想到通過高進行割補,實現轉化?轉化后的圖形怎么一定能證明就是長方形?學生怎么會想到所有的平行四邊形都可以轉化為長方形呢?經過認真思考,設計以下三個核心問題:1.可以從什么地方剪?2.該如何剪?3.為什么要這樣剪?第一個問題可以有效打破只沿頂點畫的那條高剪這一思維定勢,突破沿平行四邊形所有的高都可以剪這一思維難點。第二、三個問題能有效溝通平行四邊形與長方形之間的關聯,在師生對話、生生對話中思辨平行四邊形的轉化后得到的就是一個長方形,體會“割補轉化”的價值。學生在精心設計的核心任務的驅動下,通過師生、生生對話解決問題,在思辨中達成共識,能高效的完成核心知識的學習,提高課堂教學效率和品質。
(三)落實核心素養,培養學生思維能力
為了實現“量感”這一核心數學素養的有效落實,在組織教學實施時,我們將數方格作為驗證猜想的第一個核心任務,為了讓學生更好地經歷數的過程,感受任何圖形的面積都是面積單位的疊加,在數方格時我們沒有給出提示“不滿一格按半格計算”這句話語,一方面可以讓學生扎實地數,另一方面讓學生自己去想到將平行四邊形最左邊的角平移到最右邊轉化為長方形后來數會更好數,為后面的圖形轉化做好鋪墊。在學生沿高將平行四邊形轉化為長方形后,為了培養學生嚴密的推理能力,我們還增設了讓學生說理環節。怎么證明拼成的就是長方形,讓學生從長方形的特征入手加以辨析論證,培養學生的辨析推理能力。在應用環節為了更好地鞏固平行四邊形的面積公式=底×高,設計的兩道習題中都特別加強了底乘對應高的理解,以及不能鄰邊相乘的辨析,并用微課加以論證說明,排除錯誤知識干擾,更好地幫助學生將平行四邊形面積公式運用到實際生活中去。
責任編輯 徐國堅

