小學數學教學中數形結合思想的滲透

文｜康長華

數學是一門既抽象又具體的學科，引入數形結合思想，能將抽象的數學概念與具體的圖形相結合，通過直觀的圖形幫助學生理解和掌握數學知識，對學生的數學學習產生積極影響。

一、以形助思，培養學生的數學思維能力

數學概念是課程學習的基礎，在“分數的初步認識”課程教學中，對于“分數”概念的講解，教師可以利用圓形或正方形的模型，將分數概念具化為實際的物體，幫助學生形成分數的視覺化認知。

第一步，引導學生回憶已學過的整數知識，帶領學生回顧整數的基數、大小比較等知識點，為認識、理解分數做好基礎知識鋪墊，將整數知識和分數知識聯系，建立更完整的知識體系。

第二步，引入分數概念引導學生回憶整數的基數概念，讓學生感知分數的基數可以看作是整體的“部分”數量，使學生比較容易理解分數的概念和意義，促進對分數的理解。

第三步，將模型分發給學生，讓學生用標記筆將其平均分成4 份，其中的一份就表示，學生觀察模型布局，教師拿出其中個圓形模型并順勢引入分數的概念，寫出，并解釋它的含義。第四步，展示不同形狀的，如圓形、正方形、長方形等，幫助學生理解分數的普遍性，在學生對分數有了初步認識后，教師可以進一步深化學生對分數的理解，幫助學生更深入地理解分數的概念，明白分數的實際應用。

教師可以利用圖形比較概念。對于一些相似的數學概念，教師可以利用圖形進行比較，幫助學生區分它們的異同點。例如，學生在學習“圖形的運動”課程中容易對“軸對稱”和“中心對稱”兩個概念混淆，教師可以利用一個軸對稱圖形和一個中心對稱圖形進行比較，讓學生更清晰地理解它們的區別。

第一步，準備一些軸對稱圖形和中心對稱圖形的折紙進行示例，教師展示一個正方形（軸對稱），一個圓形（中心對稱），將正方形沿著一條對角線對折，讓學生觀察折紙后的圖形，并讓學生思考這個圖形沿對稱軸折疊后直線兩旁的部分是否重合。

第二步，把一個圓形沿著一條直徑對折，讓學生觀察折紙后的圖形，并讓學生思考這個圖形繞對稱中心旋轉180°后，前后圖形是否重合。

第三步，在展示和折紙實驗之后，教師可以引導學生比較這兩個圖形的異同點，軸對稱圖形沿對稱軸折疊后兩側圖形能夠完全重合，而中心對稱圖形繞對稱中心旋轉180°后，前后圖形能夠完全重合。借助具體的圖形展示助推學生對知識、概念的理解，幫助學生建立數學知識直觀化的意識，培養數學思維能力，學生可以更清晰地區分“軸對稱”和“中心對稱”的概念，并通過圖形比較進一步加深對它們異同點的理解，也能提高學生的辨別能力和獨立思考能力。

通過圖形可以深化學生對數學概念的理解，以形助思的方式，將數學問題中的文字描述、數量關系靈活地轉化為簡單、直觀化的圖形，幫助學生更好地理解題意，從而更快地找到解題思路和方法，培養學生的數學思維能力、發散思維能力和解決問題的能力，有效地提高教學質量和數學課堂的學習效果。

二、以形推數，提高學生的解題能力

圖形具有直觀性，能夠將抽象的數學問題轉化為具體的圖形問題，使學生更容易理解題目中的信息和問題，通過畫圖等方式可以幫助學生更好地理解題意，找到問題的突破口。通過將圖形與數學問題相互轉化，可以幫助學生更好地掌握解題方法，提高解題能力。教師可以讓學生用圖形化工具（如數位圖、方格圖等）來驗證自己的答案，從而提高解題的準確性。

例如，在“圖形的運動（二）”教學中，為了讓學生了解平移、旋轉、翻折等圖形的基本運動方式，教師可以讓學生觀察和操作圖形，預測和描述它們在運動中的變化，進而培養學生的觀察、推理和解決問題的能力。教師在課前需要準備教學工具：（1）多個圖形模型，如正方形、矩形、圓形等。（2）準備平移、旋轉、翻折等圖形運動的練習題和相關教具，如透明紙、圖形卡片等。實施教學的過程中，教師可以展示一個圖形，并問學生這個圖形有什么特點，引導學生討論圖形的運動方式。再出示一個正方形模型，讓學生通過手動操作將其平移，教師引導學生觀察并描述圖形在平移過程中位置的變化。接著，出示其他不同形狀的圖形模型，如矩形、圓形等，讓學生進行平移操作，并觀察、描述圖形的位置變化。學生對“平移”有了基礎認識后，教師可以讓學生動手操作正方形模型，將其旋轉，引導學生觀察并描述圖形在旋轉過程中的變化。教師分發其他不同形狀的圖形模型，讓學生進行旋轉操作，并觀察、描述圖形的變化特點。

在此基礎上，教師給出練習題“將圖形A 按照規定的運動方式移動到圖形B 的位置”，提供一些實際生活中的情境問題，如“小明把一個長方形蛋糕切成正方形塊，請你觀察這些塊在移動過程中會發生什么變化”，根據所學的平移、旋轉等運動規則，引導學生通過觀察圖形的形狀和位置變化，運用推理來回答問題。學生可以通過實際操作和觀察圖形的變化，深入理解圖形的運動方式，培養學生對圖形變化的直觀感知能力，提高學生解決與圖形運動相關問題的能力。

三、數形相融，強化學生自主學習意識

小學生處于形象思維為主的階段，對抽象的數學概念和算法的理解存在一定的困難，并且自主學習能力較弱，缺乏獨立思考和解決問題的能力。教師將抽象的數學問題轉化為形象生動的圖形和動畫，符合小學生的認知特點，能激發學生的學習興趣，從而提高學生的自主學習能力。

“雞兔同籠”是典型的數學題目，在《孫子算經》里，雞兔同籠問題被叫作雉兔同籠問題，原文為：今有雉、兔同籠，上有三十五頭，下有九十四足。問：雉、兔各幾何？雞兔同籠的解決方法非常多，這一課程的學習需要通過假設、利用想象來求解，能更好地訓練學生的思維能力與自主探索能力。在引導學生解決一些涉及數量關系的數學問題時，教師可以借助直觀圖形，幫助學生理解題意。將問題中的文字轉化為圖形，以便更好地理解題意，如解決關于相遇問題、追及問題等應用題時，教師可以讓學生用線段圖來顯示題目中的數量關系，幫助學生清晰地理解問題。應用數形結合思想教學，學生可以從圖形的轉換中發現其中的解題規律，拓展不同的解題思路。在教學中采用線段圖的方法來引導學生解決問題，教師先用線段表示雞和兔，空白的線段代表雞的只數，陰影線段代表兔的只數。

圖1

已知，一只雞2 只腳，一只兔子4 只腳，在上圖的基礎上，向外拓展一下，形成下面的圖形：

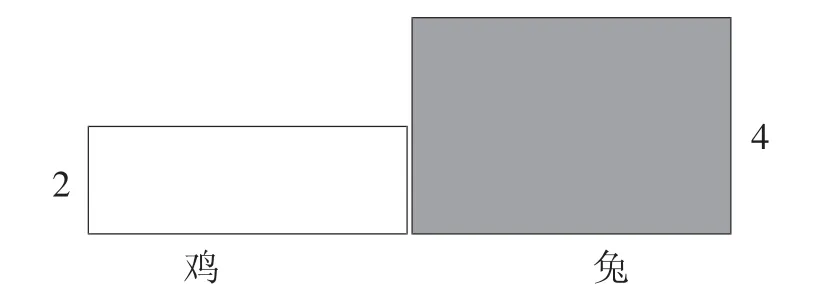
圖2

可見，空白區域的面積等于雞×2，即雞的腳數，陰影區域的面積等于兔×4，即兔子的腳數。這里有一個條件：雞和兔子的數量一共是35 只，教師可以引導學生構建出下面的圖形：

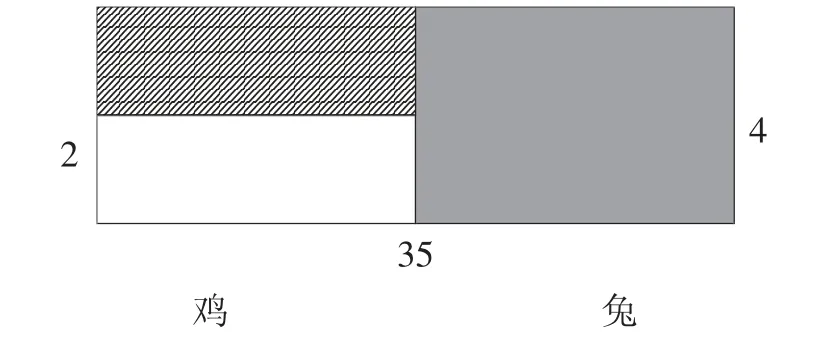
圖3

從上圖可以計算出35×4=140，是整個圖形的面積，從上面的分析中可以知道，多出來的陰影部分面積等于140-94=46，而這個長方形的寬=4-2=2，那么長就應該等于46÷2=23，也就是雞的數量，進而得出兔子的數量是35-23=12 只。

這種方法不僅計算快，還為學生拓寬了求解雞兔同籠問題的視野，從呆板單一的數字運算中，輕松地過渡到圖形的世界之中，對于啟發學生的數形結合思想，激發學生的創造力非常有幫助。這一課程對三年級學生來說，如果按照課本的知識點來講解，部分學生能夠聽懂，但是用面積的方法來講，更容易看懂，這種方法利用了數形結合思想，實質是面積概念中的“積”的應用，所謂的積就是兩個數相乘，從算式來看，就是35×4，從圖形來看，就是長35，寬4 的一個長方形的圖形面積，學生可以用圖形的面積來代表兩個數的乘積，讓學生親身體驗雞兔同籠問題的解法，解決問題的同時調動學生的探究積極性，使學生能夠自主地進行反思，拓展更多的解題思路和方法，從而讓學生養成自主探究、主動學習的習慣。

四、以圖為引，鞏固學生數學知識應用能力

教師可以將數形結合教學模式應用于課堂作業設計，借助圖形元素，學生可以更快地找到解題思路，提高解題速度和效率，并且可以激發學生的學習興趣和動力。通過觀察和分析學生的解題過程，教師可以更好地了解學生的學習特點和問題，并及時進行反饋與調整。以“圖形的運動（二）”為例，引導學生感知平移，在觀察圖形、具體操作圖形的過程中，理解平移的特點，發展空間觀念，具體設計如下。

（一）畫一畫

1.畫出左圖的另一半，使其成為軸對稱圖形。

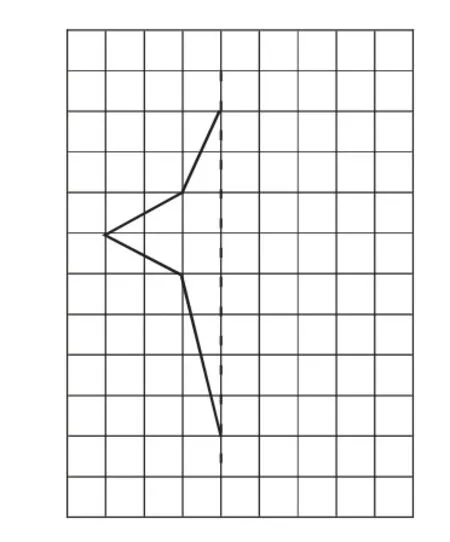
圖4

2.先畫出小樹向上平移6 格后的圖形。再畫出繼續向右平移12 格后的圖形。

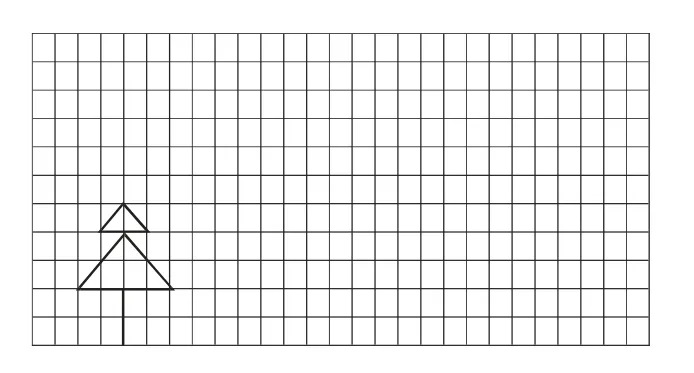
圖5

本部分是預習作業，能調動學生已有的知識儲備，喚醒學生已有的學習經驗，為新課學習鋪路搭橋，通過課前作業的反饋，教師能分析、了解學生的學情，找準學生的新知生長點。

（二）拼一拼，算一算

假設我們有一個長為4 cm，寬為3 cm 的長方形木板，如下圖所示，現在我們需要將其分割成若干個1 cm×1 cm 的小正方形。

?問題：（1）這個長方形木板可以分割成多少個小正方形？（2）如果我們將其中的一部分小正方形拼成一個新的長方形，新長方形的面積是多少？

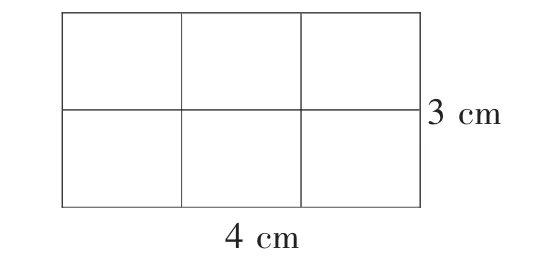
圖6

?解題分析：根據長方形木板的尺寸，可以計算出其面積是4×3=12 cm2。由于每個小正方形的面積為1 cm2，因此這個長方形木板可以分割成12 個小正方形。如果將其中一部分小正方形拼成一個新的長方形，那么這個新長方形的面積一定是12 的因數。

本題方法多樣，讓學生自己動手實踐，給予學生開拓創新的空間。

綜上所述，數形結合思想通過將數學概念與幾何圖形相結合，以圖形形式展示數學問題，以增加學生對數學知識的理解和應用能力。教師在應用過程中，需要充分發揮引導和激發學生學習興趣的作用，營造積極的學習氛圍，組織學生進行解決問題、發散思維等活動，培養學生的數學思維能力和創造力，以提高小學數學課堂教學效率。