基于“讀思達”教學法的小學數學思考力的培養

文｜吳海平

思考是思維的一種探索活動，而數學思考力是孩子在現實情境中，用數學的眼光去發現、解決問題的思維過程中產生的一種具有積極性和創造性的作用力。小學數學教學中，教師需要多方面提升學生的數學思考力。文章基于“讀思達”教學法，在小學數學課堂中用多種方式讓學生理解數學、發現數學、認識數學，從而提升學生的數學思考力。

一、以讀引思，點燃學生思考的火花

（一）建立基于閱讀的教學范式

常規課堂中經常出現下面的情況：教師用優美的導入語代替了學生對數學信息的獲取，用生動的畫面干擾學生對數學信息的思考，用自身對數學信息的解讀代替學生對數學信息的表達，用預設的結果代替學生對數學信息的解讀等。學生的閱讀被教師“替代”，那么閱讀中的發現以及驚奇體驗就沒有了。所以，轉變我們的教學模式很有必要，建立基于閱讀的教學范式，促進學生數學思考力的提升。

（二）閱讀方法的指導

語文學科有閱讀方法的指導，數學學科同樣也需要閱讀方法的指導。教師的引導可以在課堂上進行，也可以通過“導學單”進行。教師引導學生閱讀的過程，其實也是指導學生思維方法、質疑方法的過程。

比如，課前利用“導學單”，我設計以下數學閱讀步驟：第一步，初讀，篩選信息。以四年級下冊“雞兔同籠”為例，教材以古題的形式出現，通過初讀標題和內容，了解本節課的主要內容。學生弄清題意的過程也是思考的過程。第二步，精讀，弄清問題。對學生而言，教科書的內容是需要精讀的。精讀對學生來說具有一定的難度和挑戰，一般要經歷從不知道在表達什么，到似懂非懂要求的問題是什么，再到全部弄懂的過程。學生在精讀有效信息時，要弄清已知條件有哪些，是否包含隱藏的信息，待解決的問題是什么。相對而言，精讀是一個化知為智的過程。第三步，重組信息，擬定解題計劃。弄清題意后，學生會重組信息，用自己的話復述一遍題意，或者用草圖表示題意，以上也是學生思維活動的過程。第四步，回顧總結，積累閱讀經驗。在解決這道題時，產生困難的原因是什么？從這道題中可以獲得哪些經驗？從解題思路、方法、技巧和解題格式上總結經驗，拓展解題思路。

良好的開端是成功的一半。學生只有在有了一定的閱讀基礎后，才能把握題目中的關鍵信息，領會教材中的重點內容，深入思考能發散學生的思維，增強學生對知識的理解。只有經過有效的閱讀學生才能主動地去研究數學世界，用數學的思維分析、思考，讓數學思考力自然萌生。

二、以思助達，打開學生思考的大門

“學而不思則罔，思而不學則殆。”所謂的“思”是指小學生在課堂學習中，通過教師的引導，在一個個探究活動中對學習任務進行有效的交流、討論。學生得到的結論是自己探究發現的，不是教師強加的。而只有經過學生自己思考的結論才更有說服力，學生也更容易接受，在不斷地碰撞中發表自己獨到的見解，讓思維可見，從而成為打開學生思維的鑰匙，打開學生思考的大門。

（一）構建問題式的教學模式

學起于思，思起于問。在數學課堂中，教師應設計有效問題引發學生思考。問題是培養思考力的引擎。因此，基于“讀思達”教學法，我們應構建基于問題的教學范式。如果說學科方法是閱讀、思考與表達，那么，學科知識應包含知識層面、形式層面和意義層面，所以一節課可以從這三個方面進行設計主問題，即讓學生的學習從知識線索中的學習轉變為在問題解決中學習知識，助推學生數學思考力的提升。

1.知識層面的主問題

知識包括外層和內層的學科本質。這里的知識層面是一種顯性存在、感性存在，是可以直接認知的對象，是看得見、聽得見、摸得著的存在。學生通過自身認識過程中，特別是閱讀、理解中產生的困惑、疑難，從而發現、提出并解決這些疑惑，使學生的認知得到提高。以五年級下冊“兩數之和的奇偶性”為例，設計的主問題是：任意兩個整數相加，它們之和是奇數還是偶數？學生先想一想，再猜一猜，得出：偶數+偶數=偶數，奇數+偶數=奇數，奇數+奇數=偶數。學生是在讀懂的基礎上議論、猜測，而不是憑空猜測的。在思考的基礎上，與同學分享自己的猜測結果，知道兩數和的奇偶性。

2.形式層面的主問題

形式層面的知識揭示的是知識的深層意義，是學生對學習對象和內容質疑，是知識背后的認知方式和智慧價值，這是學習中最有挑戰性的問題，也是促進學生思維能力提升最大的問題。以五年級下冊“兩數之和的奇偶性”為例，設計的主問題是：怎樣驗證兩數之和的奇偶性？學生通過觀察算式和結論，思考要怎樣驗證結論？然后把自己的想法與組員交流、質疑、補充。最后全班交流提升。

組1 匯報：用舉例方法，如：

偶數+偶數=偶數，奇數+奇數=偶數，奇數+偶數=奇數

2+6=83+5=83+4=7

12+8=2023+7=3033+8=41

382+284=666895+15=910333+128=461

…… …… ……

組2 匯報：用小正方形拼擺來驗證。

偶數+偶數=偶數

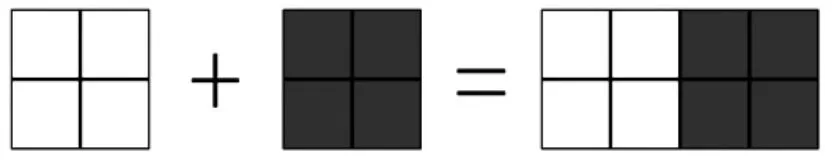
奇數+奇數=偶數

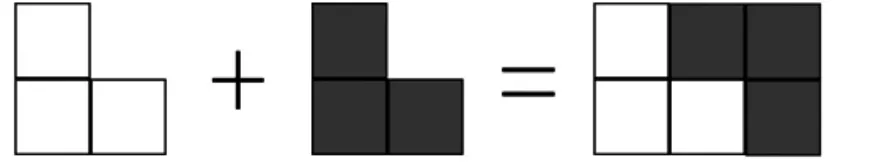
偶數+奇數=奇數

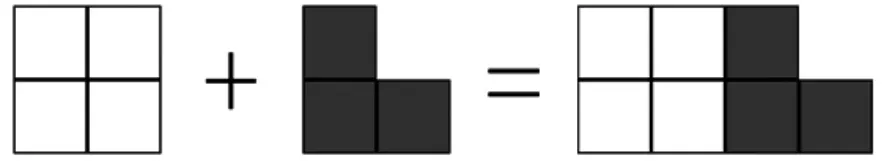
組3 匯報：根據偶數、奇數除以2 的余數來解釋，偶數除以2 沒有余數，奇數除以2 余1，偶數+偶數的和除以2 沒有余數，所以結果是偶數；奇數+奇數的和除以2 沒有余數，所以結果是偶數；偶數+奇數的和除以2 余1，所以結果是奇數。

3.意義層面的主問題

意義層面是從知識在生活中的應用價值而論。從學生的角度講，完整的學習不僅要認識、理解知識本身及其背后的思維方法，還要感悟、體驗知識的意義。以五年級下冊“兩數之和的奇偶性”為例，設計的主問題是：多數之和的奇偶性又是怎樣的？

學生通過填寫表格，觀察結果，發現規律，然后與組員交流總結：奇數個奇數的和是奇數，偶數個奇數的和是偶數，任意個偶數的和是偶數，進一步拓展延伸所學知識。

構建問題式的教學模式，學生在充分思考的基礎上內化知識，發展邏輯思維，表達思路是清晰的、有條理的、有結構的。只有當一個人親身經歷尋求問題的解決方式時，他的思維才能真正地開始。學生只有思考后說的才能更有理有據，不僅知道兩個數之和的奇偶性，還能深刻理解多數之和的奇偶性。

（二）構建育人的數學課堂

適合思考的課堂應該是自由的、緩慢的、寬容的。在實際教學中，留給學生思考的時間和空間太少，處于淺層互動的教學層面，無法進入深入的思考。在小學數學課堂教學中體現學科的育人價值，引導學生深入思考，學生才能“說”好數學，從而提升學生的數學表達能力。

1.自由的課堂，言之有力

現有的數學課堂，為了讓學生能有一個安靜的學習氛圍，個別教師總是約束學生在課堂上的行為，剝奪了學生的表達機會，這樣的課堂學生雖然看上去很乖、很有秩序，但是他們很少有獨立思考的機會。“讀思達”教學法，就是解放這種課堂，讓學生在獨立思考的基礎上通過組內的交流，使他們敢于質疑教師的觀點，引發學生的深度思考。

以四年級下冊“三角形邊的關系”為例，我給學生一段16 厘米長的線段，讓學生剪成3 段看能不能圍成一個三角形，學生發現有很多種剪法，有1，1，14；1，2，13；4，5，7；4，4，8 等多種剪法，通過共同探究發現只有剪成較短兩邊之和大于長邊時才能圍成三角形。而這一過程，正是我給學生自由發揮的空間，讓他們自由交流，發現三角形邊的關系，積累數學活動經驗，培養學生的合作、交流能力，給學生一個展示的舞臺，為學生的“言之有力”提供了良好的平臺。

2.緩慢的課堂，言之有物

教學是一門藝術，教師要留給學生足夠的思考時間，放慢腳步，靜待花開。受任務驅動，追求立竿見影，有些教師就會出現要求學生即教即學即會。接受能力較弱的學生因為沒有經過細思慢想就會跟不上教師的講解，跟上教師講解的學生對本部分知識的理解也不夠深入、印象不深，數學思維能力沒有得到進一步的提高。基于“讀思達”教學法，放慢腳步，就是把活動權交給學生，促進學生數學思考力的提升。

二年級上冊“搭配（一）”一課，正是因為放慢節奏，給了學生充分的時間和空間思考，學生出現的答案也多樣化，有的交換位置寫數：如12、21、13、31、23、32；有的先固定十位法，再考慮個位：如12、13、21、23、31、32；有的先固定個位，再考慮十位：如21、31、12、32、13、23。學生因為有細思慢想的過程，所以才會有理有據地把自己的思考過程說給大家聽，做到言之有物。

3.寬容的課堂，言之有理

錯誤也是教師教學的資源。教師如果容不得學生的錯誤，也就是容不得學生的思考，而寬容是培植學生思考力的最好沃土。有些學生因為怕講錯被教師批評，干脆就不說出自己的見解，導致所學的知識也不深刻。如果要鼓勵學生說，使學生在課堂上隨心所欲地說，就需要教師的寬容和包容。錯誤有時也是一份寶貴的資源。如學生在運用商不變的性質計算有余數的除法時，余數是幾，結果很容易出錯，會出現兩種不同的計算結果：（1）260÷30=8……20，（2）260÷30=26÷3=8……2，我沒有對學生的計算結果及時點評，而是先讓他們說說各自的想法，然后追問：怎樣驗證你們的結果是正確的？這時學生馬上會想到：被除數=除數×商+余數，發現余數應該是20。也就是被除數和除數同時除以10，商不變，余數變了，應該要還原。由此可見，允許學生大膽說出他的想法，通過對比，學生在思考后的“說”更有理有據。

學生在思考的過程中會產生很多不同的見解，從而產生表達的興趣。思是達的深度，沒有思想，所有的表達都是空口說白話。有條理的思考能夠助推學生有條理地表達，讓數學思考力和諧發展。

總之，數學教育應致力于促進學生思維的發展。在實施和使用“讀思達”教學法中，構建基于閱讀式、問題式、表達式的課堂教學模式，把培養學生的思考力擺在首位，由富有深度的數學思考對知識進行轉化、內化，學會用數學思維解決問題，促使學生的數學思考從無到有、由點及面、由單一到綜合逐步深入，以提升學生的數學核心素養，從而減輕學生的課業負擔，進一步推進“雙減”政策落地落實。