對2022年高考物理遼寧卷第14題的深入分析
王偉民
(安徽省太和縣宮集鎮中心學校,安徽 太和 236652)
從一道與類拋體運動內容有關的高考題目說起.

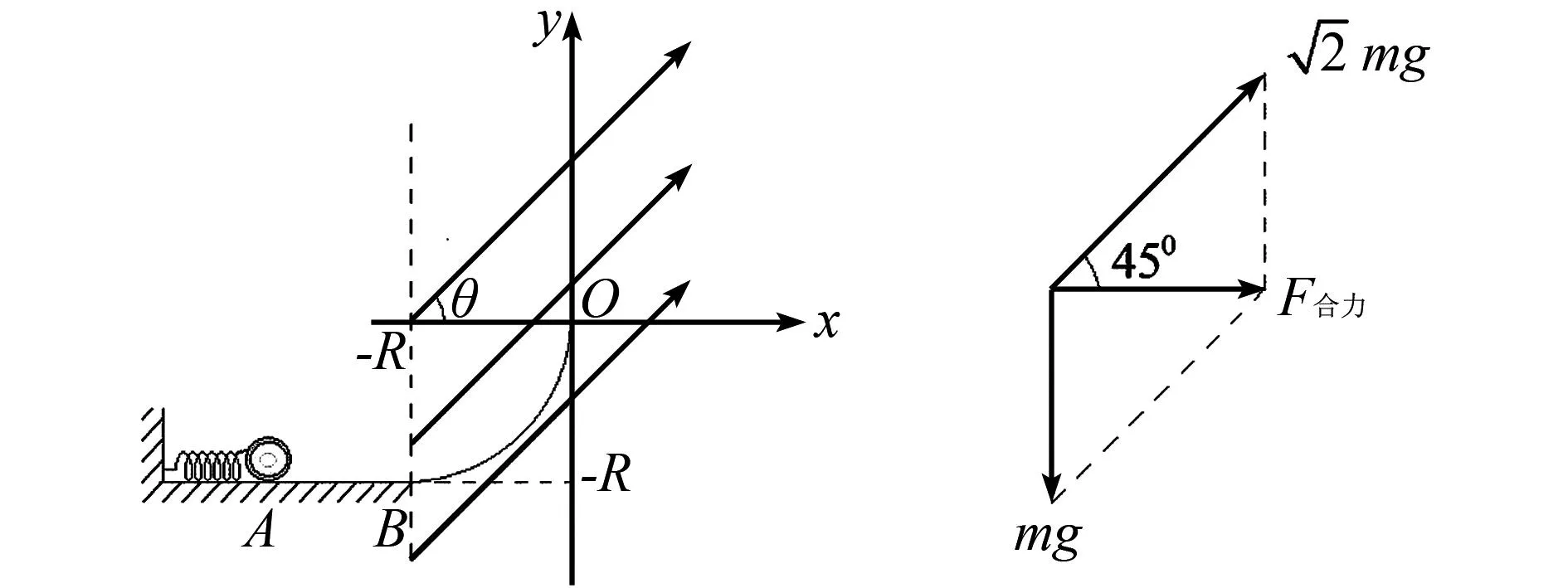
圖1 小球彈簧系統圖示
求:(1)彈簧壓縮至A點時的彈性勢能;
(2)小球經過O點時的速度大小;
(3)小球過O點后運動的軌跡方程.
1 試題簡評
這道題目是2022高考物理遼寧卷的第14題,也是整份試卷的倒數第二題,處于壓軸題目的重要位置:人們通常把一份試卷中題目難度相對較大、所占分值比例相對較高的最后兩三道題目稱之為試卷的壓軸題,它是拉開不同能力考生分數差距的題目,所以格外受到人們的關注.題目設置的物理情景是壓縮的彈簧將帶電小球以一定的速度推入勻強電場,之后在電場和重力場形成的復合場中運動,這樣設置問題把力學和電學中的多個知識點有機結合,可以綜合考查學生對電場力、能量守恒定律、動能定理、牛頓運動定律、平拋運動規律及其相關知識點的掌握情況,以及靈活應用物理知識解決復雜物理問題的能力[1].題目內容不長,只有二百多字符的內容,但卻把與所求問題相關的物理情景交代得清楚明白,通讀題目一遍,即可明晰對應的物理過程,不存在任何歧義或費解之處,體現了編者高超的原創題目的編擬水平.
2 試題解析
解析(1)因為水平地面AB是光滑的,所以,在小球與彈簧接觸并受彈簧彈力而運動的整個過程中(包含小球剛要脫離彈簧的時刻),小球與彈簧組成系統的機械能守恒,

(3)因為復合場的方向水平向右,所以,小球于O點離開光滑圓弧軌道進入復合場所在的第一象限后,作類平拋運動,運動軌跡如圖3所示.由圖2可知,類平拋運動中方向水平向右的“類拋體重力加速度”大小與重力加速度大小相同,也為g,所以,小球的運動軌跡是頂點在坐標原點,開口向右的拋物線.以小球離開O點的時刻為0時刻,時間t后,小球在坐標系內的橫、縱坐標分別為:
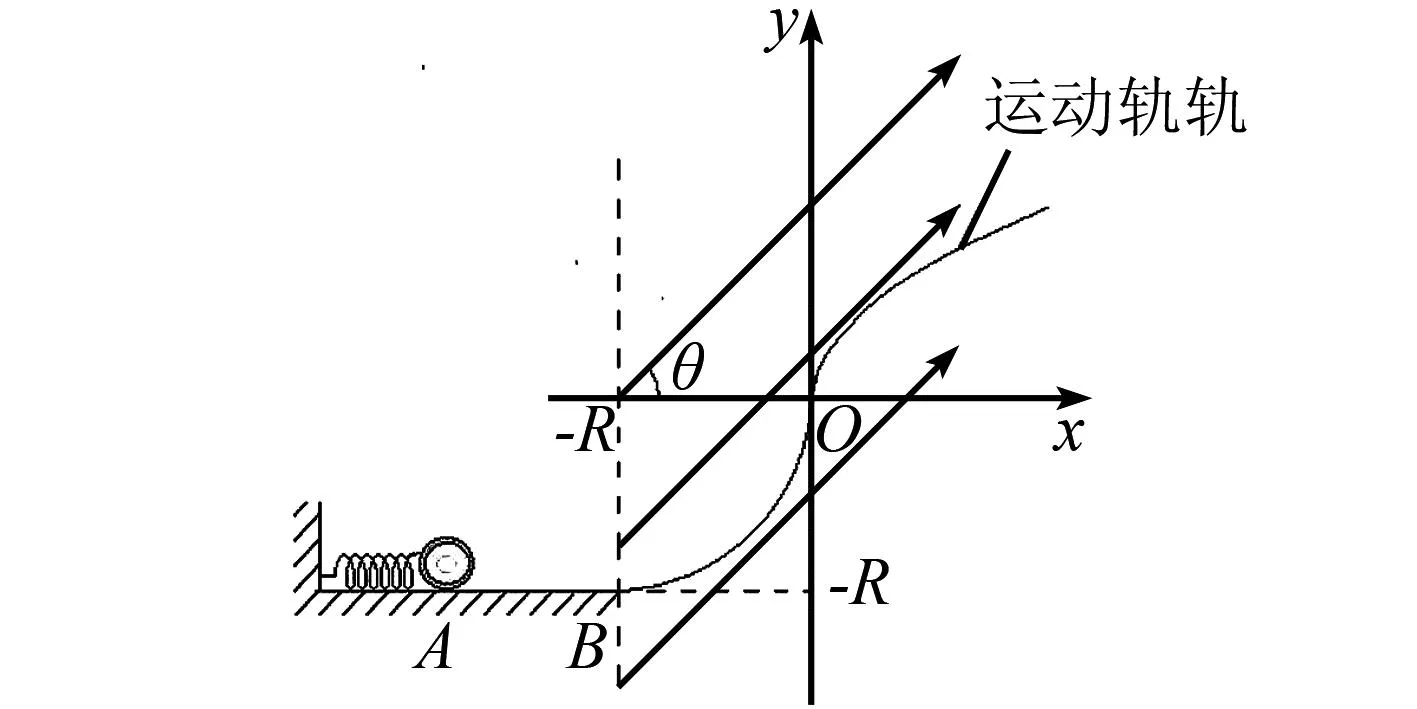
圖3 小球運動軌跡示意圖
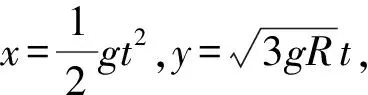
兩式結合,消去t可得到小球的運動軌跡方程為y2=6Rx.
3 試題變式
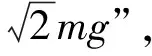
實際上,對于這道高考題目,在保持原來的物理情景(包含題設建立的物理模型)基本不變的情況下,適當改換題目條件,可以得到與這道高考題目考查知識點類似但難度更高的不同變式來.

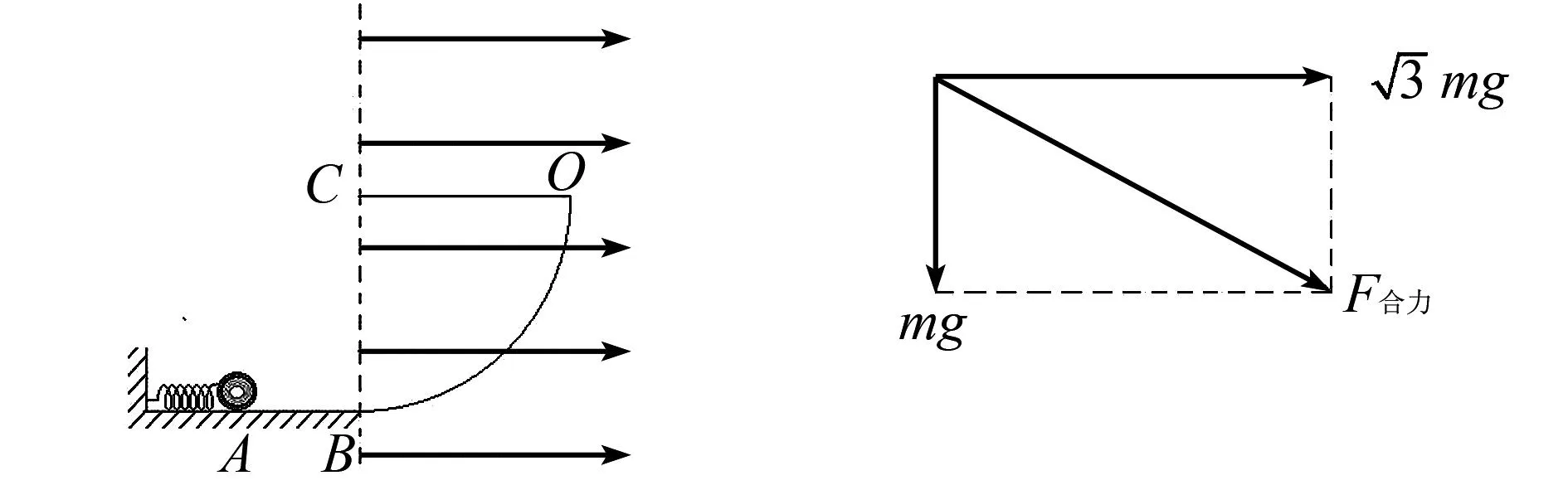
圖4 系統所在空間水平電場圖
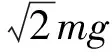
解析作出帶電小球在電場中僅受重力和電場力的受力示意圖,如圖5所示.易知,這兩個力的合力方向斜向下,與水平面成30°角,合力大小為F合力=2mg,所以,物體在復合場中的受力情形,可以等效為“等效重力場”中的受力情形,其“等效重力加速度”的方向即為圖5中的合力方向,“等效重力加速度”大小為g′=2g.
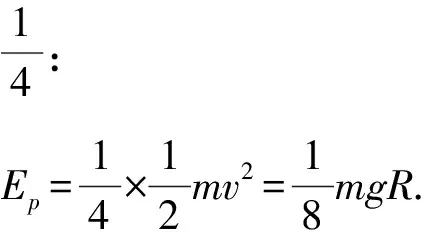
(2)因為圓形軌道是光滑的,所以小球在B點離開彈簧,進入由重力場和電場組合而成的復合場之后,其機械能守恒(這里的“機械能守恒”指的是等效重力加速度為g′=2g的等效重力場中小球的機械能守恒,在“等效重力場”中物體的“等效重力勢能”等于物體質量、物體的相對高度和“等效重力加速度”的乘積).過O點作垂直于“等效重力加速度”方向(即CP方向)的垂線ON交圓形軌道于N點,如圖6所示(為避免無關線條的干擾,圖6中水平向右的電場線沒有畫出),過B作BM⊥ON,垂足為M,顯然,OM為等效重力場中的“等效水平面”.
由幾何知識易知,△CON為等邊三角形
所以,∠CNO=60°
所以,∠BCN=30°
因此,∠CNB=75°
所以,∠MNB=45°
所以,△BMN是等腰直角三角形.
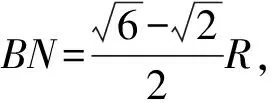
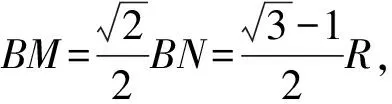
小球于等效重力場內運動過程中,在B、O兩點的等效機械能相等,故有:
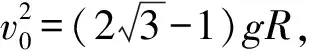
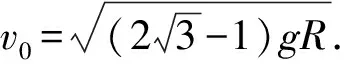
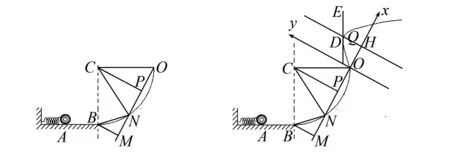
圖6 軌道添加輔助線圖示
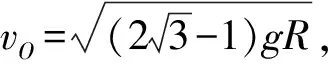
時間t后,小球在坐標平面中的橫、縱坐標分別為:
兩式結合消去t,得到小球運動的軌跡方程為:
該拋物線的頂點縱坐標為:
以x軸為等效重力場的零勢能參考面.因為小球在復合場中運行過程中,相對復合場機械能守恒,而小球運行至拋物線的頂點Q處時,距離等效重力場的“水平面”——零勢能參考面最遠,所以,小球在Q點運行速度最小.由小球在O、Q兩點機械能相等可得:,
將題目所給條件及以上推理相關結果代入可得:
(4)作拋物線在豎直方向上的切線DE(注:這里的“豎直方向”不是“等效重力場”中的豎直,而是真實重力場中的豎直),與拋物線的切點為D,顯然,D點是水平向右的電場內小球離開O點在空間運行過程中最靠左邊的點,所以,小球在D點的電勢能最大.
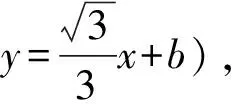
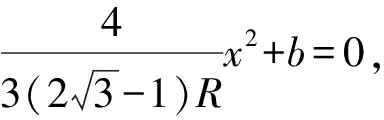
應該說,我們上面通過聯立方程組的方法進行推理得出結論的過程,雖然是可行的,但過于麻煩.還可以通過簡單的邏輯推理,得出小球在剛離開圓弧形軌道時電勢能最大的結論.因為小球是離開圓形軌道后在復合場中作拋物線軌跡運動的,所以拋物線與圓形軌道連接點O是兩曲線相切的切點,因為圓形軌道在O點的切線是豎直的,所以拋物線軌跡在O點的切線也將是豎直的,而拋物線豎直的切線只有一條,所以O點是小球運動軌跡中水平向右電場內最靠左邊的點,因此小球在O點的電勢能最大.
4 結束語
2022高考物理的第14題,巧妙設置物理模型,將力學與電學中的多個知識點有機結合起來,可以綜合考查學生對彈性勢能、機械能守恒、拋體運動等公式的掌握情況,以及靈活應用物理知識解決復雜問題的能力[3].適當改換題設條件,可以得到與原高考題目材料背景相近,考查知識點類似的不同變式,通過對變式的解析,可以使學生對同類物理問題有更為深入的理解.

