梳理圖形關系 建立內在聯系

鄭麗君 章擁軍

【摘? ?要】《義務教育數學課程標準（2022年版）》提出：要整體把握教學內容，注重教學內容的結構化。在“平面圖形的面積”總復習的教學中，教師可通過“以轉化思想為契機，引導溯源求聯；以幾何直觀為支架，啟發本質關聯；以空間想象為載體，發現內在關聯”等方式，幫助學生用整體的、聯系的、發展的眼光發現數學知識之間的內在聯系，感悟數學學習背后隱藏的思想本質。

【關鍵詞】平面圖形的面積；面積計算公式；總復習；內在聯系

《義務教育數學課程標準（2022年版）》提出：要整體把握教學內容，注重教學內容的結構化。在教學中要重視對教學內容的整體分析，幫助學生建立能體現數學學科本質、對未來學習有支撐意義的結構化的數學知識體系。平面圖形的面積是小學數學的重要教學內容。在小學階段，學生需要掌握長方形、正方形、平行四邊形、三角形、梯形和圓形的面積計算方法。這些教學內容依照螺旋上升的原則，編排在三年級到六年級的教材中。因為學習時間的跨度很長，所以學生很難整體把握和主動建立這些內容之間的聯系。六年級下冊有關“平面圖形的面積”的總復習，是幫助學生將相關知識結構化的重要契機。教學時，教師要引導學生經歷不同平面圖形面積計算公式的整理、歸類過程，建立知識網絡，體會和掌握轉化、類比、數形結合等數學思想。

基于以上認識，教師展開了“平面圖形的面積”總復習的教學實踐，用三個探究任務，引導學生將零碎的數學知識整理成一個知識系統，讓他們通過觀察、想象、思考、交流，發現平面圖形的面積計算公式推導過程中的特殊與一般的關系，感受平面圖形之間特殊與一般的關系，體會平面圖形的外在特征與內部量的屬性之間統一協調的關系。學生在學習過程中，經歷了用整體的、聯系的、發展的眼光發現不同面積計算公式之間存在著密切聯系的過程，使這些知識逐步在頭腦中形成具有統一美的嚴謹系統，產生對數學內在高度統一性的認識，以及對數學思想方法的感悟。

一、以轉化思想為契機，引導溯源求聯

“平面圖形的面積”的總復習是一節復習課。在前面幾年的學習中，學生已經陸續學習過本節課所涉及的不同圖形面積的知識點，因此，在進入課堂教學前，教師先讓學生對相關知識進行了前置性整理和復習。教學時，教師引導學生回顧已學習的平面圖形的面積計算公式的推導過程，厘清各個公式的來龍去脈，建立它們在知識結構上的內在聯系，并通過探究任務一，體會和掌握轉化的數學思想，形成對知識的一般性理解。

【教學片段1】

教師按照教材編排的先后順序，分別呈現長方形、平行四邊形、三角形、梯形和圓形，引導學生對教材中的相關內容進行梳理，交流平面圖形的面積計算公式及其推導過程，喚起學生的原認知。

師：課前，大家整理了有關平面圖形面積的相關知識。現在，我們一起來看看這個同學的整理過程，你看懂了什么？（如圖1）。

生：他是按照平面圖形的面積公式的推導過程進行整理的。

師：這些平面圖形的面積計算公式是怎樣推導出來的？你能選擇其中一個圖形說一說嗎？

生：我選擇介紹平行四邊形。推導平行四邊形的面積計算公式時，我們先通過“剪、移、拼”等方法，將平行四邊形轉化為長方形，然后根據長方形的面積計算公式得出平行四邊形的面積計算公式。

生：在將平行四邊形轉化為長方形時，我們用到的方法是割補法。而在推導三角形的面積計算公式時，我們是把兩個完全一樣的三角形拼成一個平行四邊形，再根據平行四邊形的面積計算公式推導出三角形的面積計算公式，這種方法叫作倍拼法。在推導梯形的面積計算公式時，我們也用了倍拼法。

生：推導圓的面積計算公式的過程比較復雜。我們先把一個圓沿半徑切割成若干等份，再把它們拼成一個近似的長方形，然后根據長方形的面積計算公式得出圓形的面積計算公式。

師：誰還記得長方形和正方形的面積計算公式是怎樣推導出來的？

生：我記得歸納長方形的面積計算公式時，我們把若干個1平方厘米的小正方形擺在長方形上，發現每行擺的個數相當于長，擺的行數相當于寬，所以長方形的面積=長×寬。

生：歸納正方形的面積計算公式和歸納長方形的面積公式使用的方法是一樣的。只是長方形的長和寬在正方形中是一樣的，都是正方形的邊長，這樣我們就得到了正方形的面積計算公式。

師：在這些圖形中，你認為哪個圖形的面積計算公式是最基本的？

生：我認為最基本的是長方形的面積計算公式，因為其他圖形的面積計算公式都是由長方形的面積計算公式推導出來的。

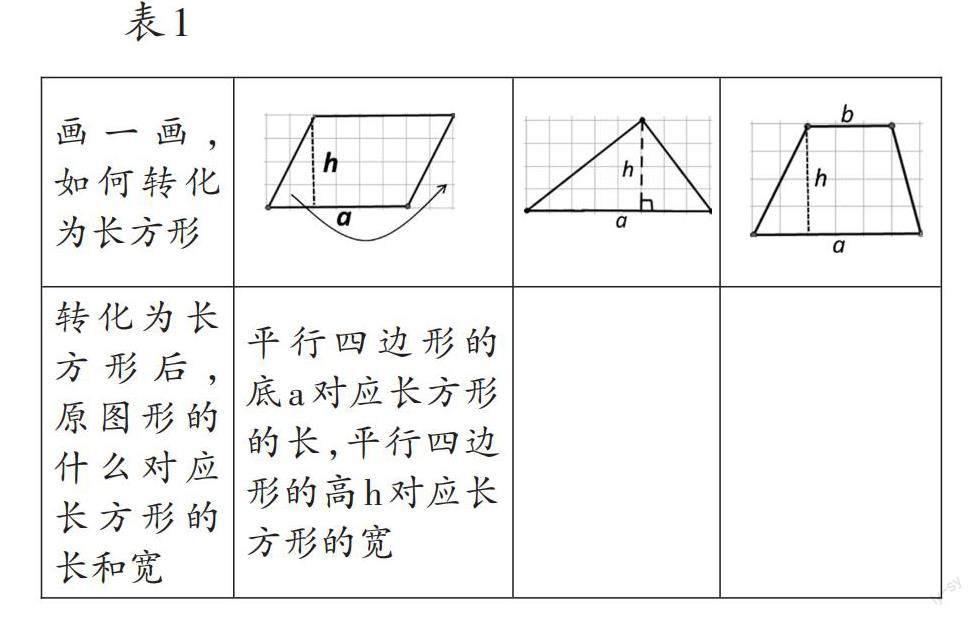
師：在學習不同圖形的面積計算公式時，只有平行四邊形是直接轉化為長方形計算面積的，轉化過程如表1。如果大家認為長方形的面積公式是最基本的，我們學過的其他圖形的面積公式都可以通過長方形面積公式推導出來，那是不是說這些圖形本身也都可以轉化為長方形呢？請大家完成探究任務一：將三角形和梯形轉化為長方形，并將表1補充完整。

學生先獨立思考、小組交流，再全班匯報。

師：三角形可以怎樣轉化為長方形？

生：我們小組把三角形的上面部分通過分割和移補轉化為長方形（如圖2）。

生：我們小組把三角形的左右兩個角通過分割和移補轉化為長方形（如圖3）。

生：其實，梯形也能通過類似的分割、移補轉化為長方形。

上述學習活動使學生對平面圖形的面積計算有了整體性的認知，在梳理中看到轉化對平行四邊形、三角形、梯形、圓的面積計算公式推導的作用，并通過再現各種平面圖形的面積計算公式的形成過程，幫助學生在梳理知識的過程中獲得對平面圖形的面積計算方法的結構化認識，形成幾何直觀、推理意識。

二、以幾何直觀為支架，啟發本質關聯

從形式上看，平面圖形的面積公式各不相同，但通過圖形的直觀變化，可以將它們統一聯系起來，從而幫助學生形成平面圖形的面積計算的知識結構。

【教學片段2】

師：剛才，我們梳理了各種平面圖形的面積計算公式，這些公式之間有怎樣的聯系呢？

教師利用課件動態演示，讓學生直觀觀察圖形的變化：一個梯形，上底開始慢慢縮短，縮短到0時，它“變成”了一個三角形；接著，它的上底再次“出現”并慢慢拉長，當上底的長度等于下底時，它“變成”了一個平行四邊形；然后，在平行四邊形的基礎上，它的“上底”從原來的位置平移到“下底”的正上方，“變成”兩組對邊相互垂直的狀態，成了一個長方形；長方形繼續變化，當長方形的長縮短到與寬長度相等時，它就“變成”了一個正方形。

師：剛才的三角形、平行四邊形、長方形等，都是從梯形“變化”而來的，那么，用梯形的面積公式是否也能計算出其他平面圖形的面積呢？

生：有可能可以。

師：請大家完成探究任務二：驗證是否可以用梯形的面積公式計算其他圖形的面積，完成表2。

學生先獨立思考、小組交流，再全班匯報。

生：可以把長方形和平行四邊形想象為上下底相等的梯形，用梯形面積公式（a+a）×h÷2計算得出面積，并將它進一步化簡，得到（a+a）×h÷2=2a×h÷2=a×h，這正是平行四邊形的面積公式。如果高和寬一致，就是長方形的面積公式S=ab。

生：同樣，把三角形想象為上底是0的梯形，就可以得到（a+0）×h÷2=a×h÷2。

生：我們原來學過，圓可以通過“化曲為直”轉化為長方形。

生：我有一個疑問。如果只用一個梯形的面積公式就能計算出這么多平面圖形的面積，那我們為什么不一開始就學梯形的面積公式？這樣不是只記這一個公式就可以了嗎？

師：這個同學太會思考了！

教師出示華羅庚的名言：先學習、接受“由薄到厚”，再消化、提煉“由厚到薄”。

師：誰能用華羅庚的名言來分析一下這個同學的疑惑？

生：先分開學習每個平面圖形的面積推導，這是知識“由薄到厚”的過程；再建立這些平面圖形的面積公式之間的聯系，找到用梯形的面積公式來計算其他平面圖形面積的方法，這是知識“由厚到薄”的過程。

在上述學習活動中，教師通過課件動態演示，借助探究任務幫助學生理解梯形、三角形、平行四邊形、長方形和正方形面積公式之間的內在聯系。

三、以空間想象為載體，發現內在關聯

空間想象是一種重要的能力。在復習階段，引導學生結合動態演示，想象平面圖形的動態形成過程，可以促進學生體會不同平面圖形之間的關聯，為他們后續的學習打下基礎。

【教學片段3】

師：我們知道“點動成線，線動成面，面動成體”，請大家完成探究任務三：想象一下，線通過怎樣的運動，會形成這些基本的平面圖形？先想象一下長方形是怎樣形成的。

生：以一條線段為長，將這條線段向上平移寬的高度，就形成了長方形。

生：也可以這條線段為寬，向左或向右平移長的距離，形成長方形。

教師用微課展示其他圖形的動態形成過程，并請學生結合動態演示過程思考：除了我們已經學過的平面圖形的面積計算公式，這些平面圖形的面積還有其他的計算方法嗎？拓展介紹：從運動的角度思考這些平面圖形的面積，它們的面積還可以通過“中位線”的長度求得。那什么是“中位線”？“中位線”怎么求呢？大家可以課后再進行探索，如果找到了答案，我們再來交流。

以上教學過程，教師通過三個探究任務，引導學生對平面圖形的面積進行整理和復習。在探究任務一中，學生以轉化思想為契機，發現了平面圖形面積推導過程之間的特殊與一般關系；在探究任務二中，學生以幾何直觀為支架，挖掘出平面圖形之間的特殊與一般的內在關系；在探究任務三中，學生以空間想象為載體，通過課內想象和課外探索，初步認識了平面圖形的外在特征與內部量的屬性之間的統一協調關系，為后續幾何的學習打下堅實的基礎。這樣的教學，能夠幫助學生用整體的、聯系的、發展的眼光發現數學知識之間的內在聯系，感悟數學學習背后隱藏的思想本質。

參考文獻：

［1］袁春胭，王霞. 圖形與幾何中數學語言表達能力發展路徑：以人教版教材《平面圖形面積的復習》一課為例［J］. 教學月刊·小學版（數學）， 2022（3）：21-23.

［2］張丹，劉曉.“問題引領學習”的構建及單元教學研究［J］.數學教育學報，2018，27（5）：42-47.

［3］劉莉.見木又見林：小學數學結構化教學的思考與實踐［J］.數學之友，2018（3）：26-29.

［4］王小權. 翻轉復習 共學悟法：“‘平面圖形面積的總復習”導學設計及實踐［J］. 教學月刊·小學版（數學），2019（1/2）：34-36.

（1.浙江省杭州市桐廬縣葉淺予建蘭學校?2.浙江省杭州市桐廬縣開放大學）