數學復習課不可缺失的思維生長力
——以“長方體和正方體的復習”一課的教學為例
江蘇省無錫市新吳區高浪小學 張 艷
小學數學復習課的教學是對一個階段學習內容進行整理反思、系統建構、對比歸納、鞏固應用的過程,從而讓學生進一步掌握數學知識,提高數學能力,發展數學素養。然而,在平時的聽課過程中,筆者發現多數教師對復習課的教學不夠重視,復習課變成了“習題操練”課、 “知識記憶”課,缺少了數學味,缺失了數學思維的生長。如何在復習課上吸引學生的主動參與,發展學生的數學思維,使學生的數學素養落地生根呢?本文結合“長方體和正方體的復習”一課的教學實踐和思考來談一談。
一、激活:已有經驗是思維生長的“土壤”
布魯納說過,學習者不應是知識的被動接受者,而應是知識獲取過程的主動參與者。對于復習課而言,也是如此,被動接受式的復習應轉變成學生主動參與式的復習,才能發展學生的思維。而復習課學習內容缺乏新鮮感,使學生不易產生學習的興趣。因此,教師可根據復習內容進行合理整合,為學生提供合適的復習材料,引領學生主動參與數學活動,在動手操作、自主探究、合作交流的過程中激活已有知識經驗,逐步觸及數學本質,使復習活動走向深入。
【教學片段一】
師:過年的時候,公園里張燈結彩地布置了起來。(課件出示花燈)你想自己設計一盞花燈嗎?我們先從簡單的做起,請你設計長方體、正方體形狀的花燈!這是老師為你們準備的材料。(如圖1)
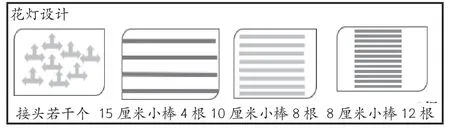
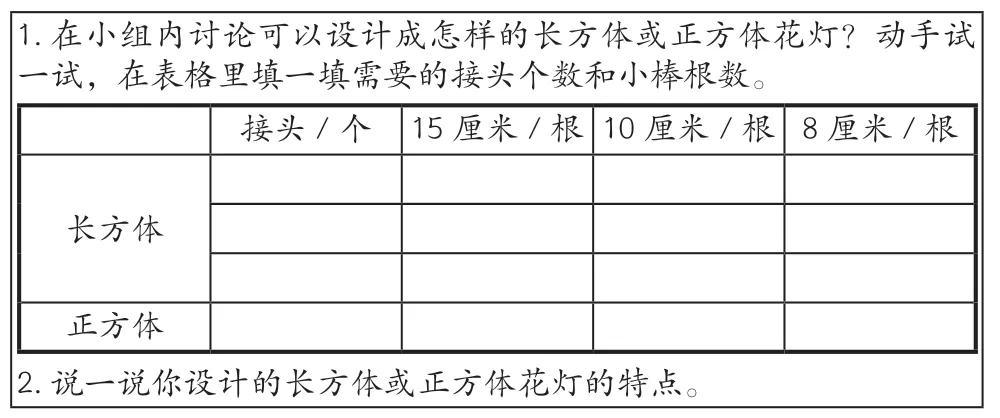
圖1
師:你選擇了哪些材料,制作了一盞什么形狀的花燈?
生1(舉著長方體形狀的花燈):用8 個接頭,4 根15 厘米、4 根10 厘米、4 根8 厘米的小棒可以做成這樣的一盞長方體形狀的花燈。
師(追問):8 個接頭是什么?你一共用了幾根小棒?
師:還有不同的嗎?
生2: 我用8 個接頭,8 根8 厘米、4 根15 厘米的小棒做成這樣的花燈。
師:你設計的花燈和剛才那名同學的相比,有什么特別之處?
生2:我的花燈兩個相對的面是正方形,其余四個面完全相同。
生3:我用8 個接頭,12 根8 厘米的小棒可以做成正方體形狀的花燈。
生4:利用這些材料可以做成四種不同的長方體,其中一種是正方體。
師:同學們都很厲害,手腦并用,利用有限的材料設計不同形狀的花燈。
師(追問):同學們有沒有發現,剛才大家做的花燈在選材上有什么相同之處?
生1:這些長方體或正方體形狀的花燈都有8 個接頭、12 根小棒。
生2:因為不管是長方體,還是正方體,都有8 個頂點、12 條棱。
師:真會總結,仔細觀察,大家發現它們有什么不同嗎?
生3:長方體同一頂點的三條棱長度不相等,正方體同一頂點的三條棱長度相等,特殊的長方體同一頂點的三條棱中有兩條是長度相等的。
生4:一般的長方體有三種不同長度的棱,每種4根,特殊的長方體有兩種不同長度的棱,分別是4 根和8 根,正方體的12 條棱都相等。
對于學生來說,他們剛接觸長方體和正方體這樣的立體圖形,空間想象能力較弱,借助有形的材料有助于其空間觀念的建立。教師創設的設計花燈的活動不僅激活了學生關于長方體和正方體特征的經驗,而且用開放的數學問題兼顧了各種認知水平的學生。學生可以設計一種,也可以設計幾種。設計花燈的過程其實是對立體圖形重新建構的過程,是有思維含量的操作過程。同時,充分的互動交流使學生的經驗被不斷激活,數學知識愈加清晰,思維得到有效的訓練和發展,也為后續的復習做好鋪墊和準備。
二、求聯:溝通想象是思維生長的“觸角”
“基礎知識貴在求聯,基本技能貴在求通。”鄭毓信教授的這句話指出了復習課的核心目標。教師需要充分了解知識之間的聯系,除了對橫向知識的掌握,還要著眼于縱向知識之間的連貫性。“知所先后,則近道矣。”教學中,教師要幫助學生追溯數學知識的本源,從系統的角度出發,準確把握知識的“前世今生”,通過溝通和想象的方式讓思維的觸角引導學生感悟知識之間的本質聯系,進而使學生對所學知識融會貫通。
【教學片段二】
老師的相機記錄下了同學們做花燈的過程。(出示圖2)
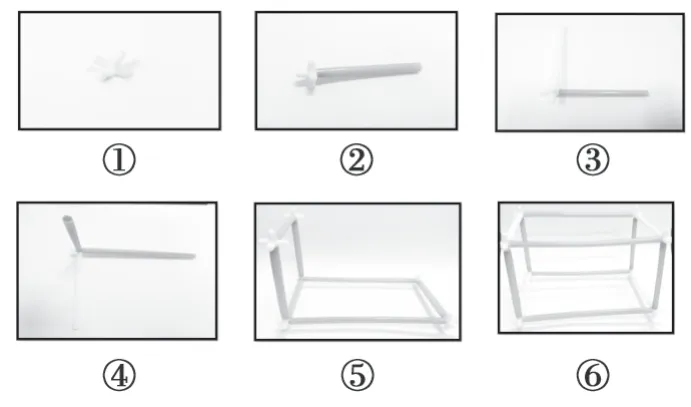
圖2
師:仔細瞧,至少從圖中哪一步可以確定這盞花燈的形狀?
生:至少從圖中第④步可以確定這盞花燈的形狀,因為圖中第④步確定了長方體的長、寬、高。
師:是的,相交于一個頂點的三條棱確定了,長方體的形狀也就確定了。(指屏幕)看,做花燈的過程其實就是從點到線、線到面,最后到體的過程。是不是很神奇?
師(出示圖3):花燈的框架搭好了,你能給這三盞花燈挑選合適的花燈布嗎?
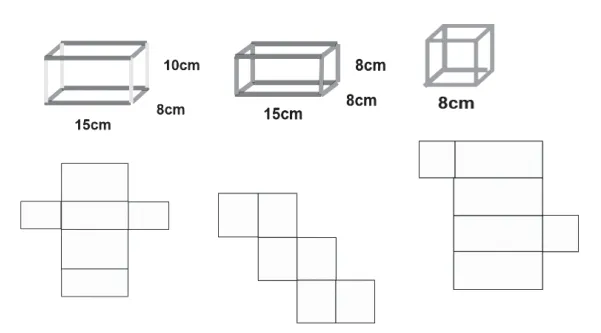
圖3
師:選一選,你是怎么看的?
物種累積曲線被廣泛應用于判斷試驗設計取樣量是否充分以及估計物種豐富度(李巧,2011)。為了驗證本次野外試驗獲取的數據是否具代表性,利用EstimateS 9.1.0對數據進行檢驗并制圖。如果曲線一直上升,表明樣本量不足,需增加試驗;如果曲線最終變為漸近線,上升平緩,則表明抽樣充分,可對數據作進一步分析(李巧,2011;Longino,2000)。
生:長方體相對的面完全相同,正方體的6 個面都是正方形。
……
長方體和正方體屬于立體圖形,在此之前,學生已經學習了長方形、正方形等平面圖形。在上述教學中,教師巧妙借助學生做花燈的流程圖,通過局部想整體,幫助學生建構點、線、面、體的聯系。接著,通過給花燈選花燈布,又通過三維立體圖形想象二維平面圖形,在多次的轉換、想象中,學生不僅深入體會數學知識的本質,而且發展了空間觀念。
三、梳理:系統建構是思維生長的“支架”
學生數學知識的學習過程,是一課時一課時累加學習的過程,很難看到知識的整體脈絡。因此,在復習課中,教師要引導學生運用思維導圖、表格、列舉等形式對知識進行系統的歸納和梳理,以尋求知識之間的聯系和區別,從而把所學知識放到一個整體中來系統理解,體驗知識之間的脈絡,構建完整的知識網絡。
【教學片段三】
師:回憶一下這學期我們學了關于長方體和正方體的哪些知識?你能把這部分知識梳理一下嗎?
(學生在小組內自主梳理)
這一單元知識點多、碎、雜,教師通過引導學生自主梳理,把重要的知識點,如長方體和正方體的特征、表面積和體積等通過表格的方式概括性地串聯在一起,由點帶到片,由片鋪成面,形成顯性的知識結構,使學生在原有知識的基礎上獲得延伸和發展,建構屬于自己的認知體系。
四、應用:對比遷移是思維生長的“助力”
鞏固應用是復習課的重要環節,練習的設計與教學要體現學生原有知識水平上的提升和發展。教師需要根據復習內容進行巧妙的整合,利用題組練習、變式練習、開放練習等形式打破學生思維的壁壘,靈活運用對比、遷移等方法訓練學生綜合運用知識靈活解決實際問題的能力,培養學生提出問題、分析問題、解決問題的能力,讓學生在自主經歷解決問題的過程中逐步形成思維品質和質疑意識。
【教學片段四】
1.解決正方體禮盒的問題
師:瞧,這是一個正方體禮盒,你能提出哪些數學問題?
生1:這個禮盒需要包裝紙的面積是多少?生2:正方體禮盒的容積是多少?
生3:包扎禮盒需要的彩帶長是多少?
師:你能解決這些問題嗎?
(點名學生回答,只列式不計算)
2.解決長方體魚缸的問題
師:這是張老師家最近新買的魚缸,你能幫我解決這些問題嗎?請小組內說一說每個問題和什么有關,再完成。
師:你覺得在運用長方體和正方體的知識解決實際問題時要注意什么?
師(小結):在解決實際問題時,我們先要審清題意,弄清問題和什么有關,再結合實際情況靈活解決問題。
3.一張紙的聯想
師:這是一張紙,你能想辦法把它變成一個長方體嗎?試試看!
生1:我用折一折的方法,長方形的長是長方體的底面周長,寬是長方體的高。
師:還有不同的折法嗎?
生2:我的折法,長方形的寬是長方體的底面周長,長是長方體的高。
師(追問):仔細觀察這兩種方法,得到的長方體有什么相同和不同之處?
生3:長方體的側面積相同,體積不相同。
師:你真是個善于思考的孩子!還有不同方法嗎?
生4:我用剪一剪的方法,在長方形的四個角上剪掉四個一樣的正方形,可以折成一個無蓋的長方體。
師(追問):長方體的長、寬、高和原來的長方形又有什么關系呢?
(學生回答略)
生5:老師,我用移一移的方法,把長方形紙向上平移,平移前到平移后經過的部分就是一個長方體。
師:你很有想象力!同學們想一想還可以怎么移?長方形紙可以看成長方體的什么?垂直平移的距離可以看成長方體的什么?
(學生回答略)
在以上教學片段中,教師設置了兩個綜合性練習,其中的開放性練習包括長方體和正方體的棱長、表面積、體積、容積等知識,覆蓋面廣,綜合性強。題組的設計便于學生深入理解數學知識的本質內涵,將其遷移到生活中更多相關問題的思考和解決中,起到舉一反三的效果。教師還注重發展學生的問題意識,培養學生提出問題、分析問題、解決問題的能力和反思意識。開放性練習中對一張紙的聯想,打開了學生思維的閘門,進一步聯通了二維與三維的空間轉換,發展了學生的空間觀念,拓展了學生的思維。
總之,小學數學復習課的教學要摒棄隨意和低效,要真正做到以生為本,關注學生數學思維的生長。教師需要充分把握教材,創造性地整合復習內容,提供有形、鮮活的復習材料,引導學生主動參與,激活已有經驗,溝通知識之間的聯系,建構數學知識網絡,綜合解決實際問題,使學生的數學思維和數學素養在復習課上得到有效發展。

