基于滑窗OPTICS算法和DATA-SSI算法的橋梁模態參數智能化識別
陳永高, 鐘振宇,2, 羅曉峰,2
(1.浙江工業職業技術學院 建筑工程學院,浙江 紹興 312000; 2.浙江大學 建筑工程學院,杭州 310058)
橋梁結構在環境激勵的長期影響下,尤其是在地震作用下,其結構自身的耐久性和安全性將受到不同程度的影響[1]。現階段,關于橋梁結構健康監測的相關理論和方法已基本成熟,其中模態參數識別算法[2]已被廣泛運用于結構動力分析中,其基本原理是:先利用傳感器采集結構的振動信號,再采用相關算法對信號進行數據分析處理以獲得結構自身的模態參數(固有頻率、阻尼比及模態振型)[3],最后通過對這些參數結果做對比分析以辨識結構的實際運用狀態。
現階段,基于數據驅動的隨機子空間(data-driven stochastic subspace identification, DATA-SSI)算法[4]被廣泛運用于識別橋梁結構的模態參數,但隨著眾多學者對該算法的深入研究,發現其主要缺陷在于需人工辨識穩定圖中的真假模態[5],這樣不僅降低識別效率,還影響結果的準確性。
關于如何改進現有的DATA-SSI算法,已有不少學者進行了相關研究,包括:Bakir[6]提出可基于模態相位來對模態參數結果進行一定的量化,實現穩定圖中真假模態的自動化篩選;孫國富[7]將多參考點最小二乘復頻域法(poly reference least squares complex frequency, P-LSCF)運用于辨識穩定圖中的真假極點。同時,不少學者通過將聚類算法[8]引入到模態參數中來實現模態的智能化篩選,包括: Ubertini等在模態參數識別算法中引入聚類分析算法;姜金輝等[9]在穩定圖分析中引入模糊聚類算法,以選取每類最佳極點作為最終的結構真實模態;湯寶平等[10]在模態參數識別過程中引入譜系聚類算法;李玉剛等[11]在模態參數識別過程中引入K-means算法(K-均值算法,是一種基于劃分的聚類算法,以距離作為數據對象間相似性度量的標準);單豪良等[12]通過將DBSCAN(density-based spatial clustering of application with noise)密度聚類算法運用到確定隨機子空間算法中,以實現穩定圖中模態參數的自動化識別。經分析,這些算法均處于半自動化狀態,主要原因在于需人為提前就聚類數目或迭代次數等相關參數進行設定。
為實現環境激勵下橋梁結構模態參數的全智能化識別,本文提出對DATA-SSI算法的輸入信號進行合理的滑窗處理,再結合OPTICS(ordering points to identify the clustering structure)密度聚類算法實現眾多穩定圖中穩定軸的聚類處理,以達到實際橋梁結構模態參數在線智能化識別的目的,提高參數識別的效率和準確性。
1 密度聚類算法
聚類算法之所以被廣泛應用于穩定圖中真假模態的辨識,主要是因為該算法是一種無監督機器學習算法,可以將具有相同特征的數據聚集為一類,將特征相異的數據分開。現階段,常用的三種聚類算法包括:
(1) 分層聚類算法:基本原理是對所有數據進行逐層分類處理,直到聚類所得結果滿足人為事先確定的某種條件為止。
(2) 劃分聚類算法:基本原理是對所有數據進行簇數的預設劃分處理,并假定各簇數的中心點,同時對該中心點進行更新,通過反復迭代的方式使得同一簇種的數據特征相近,非同簇中的數據特征相異,直至中心點不再更新為止。(需要事先指定簇類的數目或者聚類中心,通過反復迭代,直至最后達到“簇內的點足夠近,簇間的點足夠遠”的目標)。
(3) 密度聚類算法[13]:基本原理是通過相關算法實現空間中密集點和稀疏點的辨識,將緊密地在一堆的點組合起來,將其它點定義孤立點。
經對比分析三種聚類算法各自的優缺點,本文選擇密度聚類算法作為基礎算法,該算法相比其它兩種算法的特點在于:密度聚類不會因為所需聚類數據的增加而降低聚類效果,且所需確定的初始參數最少,對數據的先后順序無具體要求,能處理高維度的數據。
單豪良等所提算法雖然能在一定程度上提高模態參數識別的精確性,但其依然存在缺點,即該算法中鄰域半徑(Eps)為定值,當所需聚類的數據點密度存在不均勻現象時,一旦設置的Eps數據較小,將會導致較稀疏的聚類簇中的節點密度會小于密度閾值(MinPts),則其會被認為是邊界點;當設置的Eps數據較大時,將會導致較密集且離得比較近的簇點容易被劃分為同一個聚類簇。
鑒于穩定圖中的數據點為高維數據(包括固有頻率值、阻尼比及模態振型),且數據點呈現密度不均的現象,所以采用DBSCAN算法[14]具有一定的局限性。于此,本文將引入OPTICS算法[15],該算法實質上是DBSCAN的一種有效擴展,兩種算法的基本思想是相同的,但OPTICS算法使得基于密度的聚類結構能夠呈現出一種特殊的順序,該順序所對應的聚類結構包含了每個層級的聚類的信息,且便于分析,使得聚類結果對輸入參數不再敏感。
以下將首先分析OPTICS算法中的相關定義,其次詳細介紹該算法涉及的Eps和MinPts,最后簡要介紹該算法的實現流程。
1.1 OPTICS算法的相關定義
假定數據集X={x(1),x(2),…,x(N)},涉及的兩項參數分別為鄰域半徑(Eps)和密度閾值(Mpts)。
定義1:鄰域半徑。該半徑是以點P為中心點,滿足
NEps(p)={q∈X|d(p,q)≤Eps}
(1)
定義2:距離。點q與點P間的距離值d(p,q),其中p=(p1,p2,…,pn),q=(q1,q2,…,qn),鑒于兩對象為一維向量數據集,可采用歐幾里得函數求解距離值
(2)
定義3:核心對象。基于式(1)計算數據集X中的對象P的鄰域半徑,當滿足式(3)時,可判定該對象為核心對象。
|NEps(p)≥Mpts|
(3)
定義4:核心距離。假定x作為核心點,找到以x點為圓心,且剛好滿足最小鄰點數Mpts的最外層一個點為x′,則x點到點x′的距離為核心距離。數學定義如下
(4)

定義5:密度。假設x∈X,ρ(x)代表x的密度,取值為整數值,且與鄰域半徑存在直接關系,滿足
ρ(x)=|NEps(x)|
(5)
定義6:密度直達。若q∈NEps(p),并滿足式(3),則稱q密度直達p。
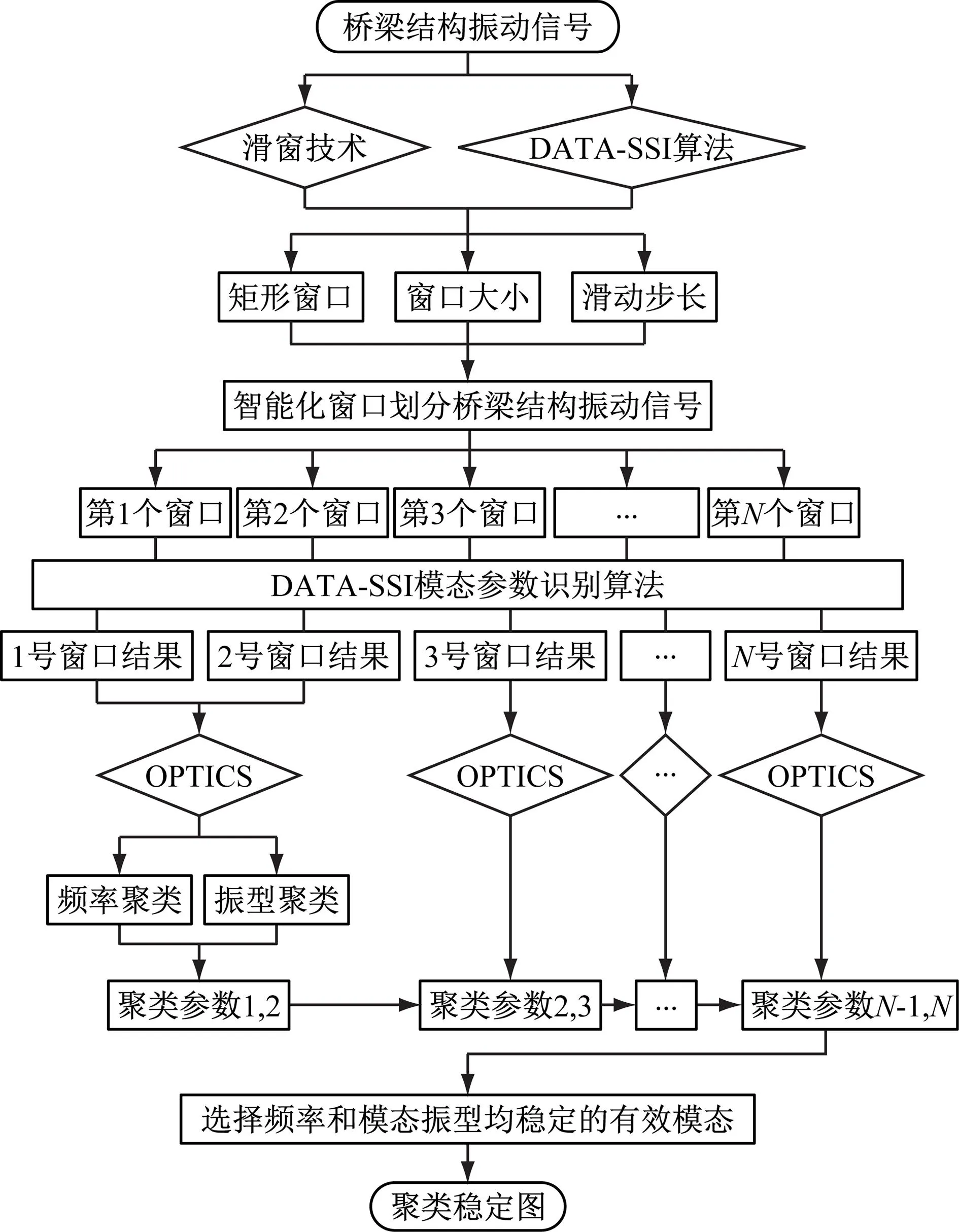
定義7:密度可達。若存在鏈p1,p2,…,pn∈X,其中,pi(0 定義8:密度相連。若對象o∈X,使得p從q是從o密度可達的,則定義p和q是密度相連的。 定義9:簇。非空集合C滿足C?X,并滿足如下兩條件,可將非空集合C定義為X一個簇: (1) 若p∈C,且q是從p密度可達,則q∈C (2) 若p∈C,q∈C,則p,q屬于密度相連 定義10:噪聲點。若p不屬于任何一個簇,則其為噪聲點。 (1) 鄰域半徑閾值 相比DBSCAN算法,OPTICS算法對輸入參數并不敏感,即可將其取值定義為式(2)計算所得距離值d(p,q)的最大值,代表所有的點都屬于核心點。 (2) 密度閾值 在確定該閾值前,需對穩定圖方法進行一定了解,穩定圖方法的基本原理——無需事先預估結構系統的真實模態階數,是通過假定該結構系統存在很多不同的階數,并分別計算各階次情況下結構的模態參數結果,最終以模態參數結果為橫坐標,系統階數為縱坐標。因為結構的真實物理模態具有穩定性,會一直以相似的模態重復出現,并在二維圖形中形成豎向的穩定列,被定義為穩定軸;而虛假模態具有不穩定性,呈現隨機出現的狀態,以致無法形成穩定軸。 為保證篩選出的穩定軸為“結構的真實穩定”,結合統計學中的置信區間[-0.95,0.95],構建式(6)確定密度閾值 Mpts=INT[(Jmin-Jmax+1)×0.95] (6) 式中:Jmax和Jmin分別為穩定圖中系統階次的最大值和最小值;INT[·]為取整數。 對于數據集X={x(1),x(2),…,x(N)},OPTICS算法的目標是輸出X數據對象的兩個特征,即輸出次序和可達距離,具體如下: 采用OPTICS算法對數據集進行聚類處理時,具體實現流程如下: 步驟1:準備階段 設定鄰域半徑(Eps)和密度閾值(Mpts)。 步驟2:實施階段 (3) 確定該點直接密度可達的點中可達距離最小且未處理的點,并將其列入結果隊列中。 (4) 重復步驟2中的第(2)步,直到該點直接密度可達的點均被處理。 (5) 處理完數據集中所有點,賦予第一個點的可達距離為其它點中最大可達距離的1.1倍,算法結束。 實際工程中,若僅常用OPTICS算法對單幅穩定圖所對應的模態參數結果進行聚類,則聚類所得真實模態不具代表性,且無法真實反映結構在長時間內的真實模態。因此,可通過識別同一結構在連續時間段內的多幅穩定圖,以總結真實模態在各穩定圖中存在的規律。為實現連續時間段內的模態參數識別,需對輸入信號進行合理的劃分,以下將從三個方面詳細論述如何實現信號的合理窗口劃分,包括窗口函數的確定,窗口大小的確定以及窗口滑動步長的確定。 矩形窗函數相比其它窗函數(漢寧窗、海明窗及平頂窗等)而言,具有簡單易操作的特性,同時其時間變量屬性為零次冪,主瓣會更集中,識別穩定圖中的數據點具有可行性。 矩形窗函數公式如下 w(t)=1 (7) 基于DATA-SSI算法的參數識別,當被識別的信號過長時不僅耗時,且容易識別出虛假模態;當被識別的信號過短時,則容易出現真實模態漏判的現象。因此,可通過如下流程確定單次模態參數識別的合理信號長度: (1) 任意假定初始的1號窗口Win1=(x1,x2,…,xn),xi代表該窗口中的第i個數據點,共有數據點n個。 (2) 采用DATA-SSI算法識別窗口Win1,得到模態參數結果R1={f1,ξ1,ψ1} f1=f1(m,n), ξ1=ξ1(m,n), ψ1=ψ1(m,n,q), m=1,2,…,M, n=1,2,…,N, q=1,2,…,Q。 (8) 式中:f1、ξ1、ψ1分別為窗口Win1的頻率值、阻尼比及模態振型結果;(m,n)為頻率和阻尼比結果為二維數據矩陣;(m,n,q)為模態振型結果為三維數據矩陣;M為頻率矩陣中最大的行數;N為結構的真實系統階數;Q為布置在結構上的總傳感器個數。 (3) 提取并保存第1階頻率值f1-1=f1(1,i)(i=1,2,…,N)、第2階頻率值f1-2=f1(2,i)(i=1,2,…,N)、第3階頻率值f1-3=f1(3,i)(i=1,2,…,N)。 (4) 對窗口Win1進行擴展(增加窗口內的信號長度)得到2號窗口(Win2),并基于步驟(2)和(3)識別得到Win2的前三階固有頻率模態值f2-1,f2-2,f2-3。 (5) 對窗口進行不斷擴展,并基于上述相同的原理,依次得到各自窗口對應的前三階固有頻率值,假定窗口Wini的前三階固有頻率模態值為fi-1,fi-2,fi-3。 (6) 交替求解相鄰兩窗口前三階頻率模態值的相似度,以計算1號窗口第1階頻率值(f1-1)和2號窗口第1階頻率值(f2-1)為例,通過式(9)得到1號和2號窗口頻率參數結果在第1階的相似度f(1,2,1)。 (9) 假定f(i,i+1,l)為第i號和第i+1號窗口頻率參數結果在第l階(l=1,2,3)的相似度。基于統計學中95%置信區間的原理,尋求當連續4個窗口對應的3個相似度[f(i,i+1,l),f(i+1,i+2,l),f(i+2,i+3,l)](l=1,2,3)均處于95%時,即代表窗口大小的改變已不再會引起頻率值的變化,則可確定Wini對應的合適的窗口大小。 當窗口大小確定后,還需進一步確定相鄰兩窗口之間的滑動步長,即確定后一個窗口與相鄰前一個窗口之間的重疊占比。鑒于DATA-SSI算法在計算Hankel矩陣[17]時,將過去和將來的信號設定為相等的長度,因此,本文將滑動步長設定為每個窗口的一半長度。窗口滑動步長示意圖,如圖1所示。 圖1 窗口滑動步長示意圖Fig.1 Schematic diagram of window sliding step 實際工程中,若僅采用DATA-SSI算法識別結構模態參數,則需面臨穩定圖中穩定軸需人為參與辨識的問題,以致存在如下問題: (1) 因不同用戶自身對穩定圖認知的程度不同,導致在篩選真假模態時出現一定的主觀性和差異性。 (2) 當需要對大量穩定圖進行人工識別時,其工作效率不高。 (3) 因無法實現穩定圖中真實模態的智能化辨識,以致無法實現對實際結構進行在線實時監測。 針對傳統DATA-SSI模態參數識別算法存在的上述弊端,本文結合“滑窗機制原理”和“OPTICS算法”提出了一種新的模態參數識別算法ICDATA-SSI(identify clustering data-driven stochastic subspace identification),以實現模態參數在線實時監測的目的。具體實現步驟如下: 步驟1:數據集準備 假定布置在橋梁結構上的傳感器個數為Q,收集并儲存結構對應的所有振動信號X=(i,j)(i=1,2,…,L;j=1,2,…,Q),其中L為信號采集時間段(T)內的數據點數,假定fs為采樣頻率,則: L=T×fs (10) 步驟2:窗口數據準備 (1) 以X=(i,j)為信號滑窗對象,提取其中最靠前的一段時間T1(以“秒”計)對應的數據點為1號窗口,得到數據集Win1=(i,j),滿足式(11) i=1,2,…,T1×fs j=1,2,…,Q (11) (2) 基于2.2節原理,確定最佳的窗口大小,假定最佳窗口大小對應的采樣時間為Ts,即每個窗口的數據點數BC=Ts×fs。 (3) 確定總的窗口個數NN,公式如下 (12) 式中,INT[·]代表取整數。 (4) 確定窗口滑動步長為BC/2。 步驟3:各窗口模態參數計算 采用DATA-SSI算法對NN個窗口對應的振動信號進行模態參數識別,并儲存所有的模態參數結果Ri={fi,ξi,ψi}(i=1,2,…,NN)。 步驟4:單次聚類分析 1) 頻率聚類 (1) 頻率鄰域半徑計算 采用式(11)計算兩模態中頻率值間最遠的距離,并將其定義為頻率鄰域半徑,以保證穩定圖上的所有點均為核心點,公式如下 Eps=max[d(f1-1,f2-1)]= (13) 注意需結合式(8)進行上述計算。 (2) 密度閾值計算 (3) 頻率聚類結果 i=1,2,…,N (14) 式中,N為結構的真實系統階數。 2) 模態振型聚類 (1) 振型鄰域半徑計算 因模態振型的組成不同于頻率值,頻率值為具體的數據,而模態振型涉及特征向量,需重新計算模態振型參數對應的鄰域半徑(Eps)。可采用式(15)計算兩模態中模態振型間最遠的距離,并將其定義為振型鄰域半徑,以保證穩定圖上的所有點均為核心點,公式如下 Eps=max[d(ψ1-1,ψ2-1)]= (15) (2) 模態振型聚類結果 i=1,2,…,N (16) 式中,N為結構的真實系統階數。 步驟5:1號和2號窗口間多次聚類分析 步驟6:相鄰窗口間多次聚類分析 步驟7:匯總聚類結果 (2) 結合統計學中兩數據相似的判別原理,可認定每一階對應的聚類窗口的個數占比大于等于 0.8Nmax時,可將該階模態定義為結構的真實模態。 (3) 計算各階次真實模態中頻率值在所有聚類窗口中的“平均值”,并繪制于穩定圖中,獲得最終的聚類穩定圖。 綜上可知,經過步驟1~步驟7便能實現滑窗技術、OPTICS聚類算法及DATA-SSI識別算法的有機結合,實現橋梁結構模態參數的智能化識別。為更直觀地反映各步驟間的相互關系,繪制了圖2所示流程圖。 圖2 ICDATA-SSI模態參數智能化識別流程圖Fig.2 Flow chart of intelligent identification of ICDATA-SSI modal parameter 為驗證本文所提算法能有效識別穩定圖中的真實模態,現通過MIDAS軟件建立一跨鋼筋混凝土簡支梁作為試驗對象。簡支梁橋長30 m,主梁共10個單元;橋面寬930 cm,梁高170 cm,梁底寬460 cm,截面為單箱單室,具體尺寸如圖3所示。 (a) 簡支梁橋 (b) 截面圖(cm)圖3 簡支梁橋模型Fig.3 Mode of simply supported girder bridge 為獲取該簡支梁的振動響應信號,可在主梁各單元銜接點處施加豎直向下的白噪聲激勵,以模擬實際工程中的環境激勵。其中采樣頻率為100 Hz,采樣時間為10 min,圖4為第1分鐘白噪聲激勵的時間曲線圖。 圖4 白噪聲激勵(第1分鐘)Fig.4 White noise excitation (in the first minute) 采集各節點在白噪聲激勵下的振動響應信號,圖5為其中3號節點、6號節點及9號節點對應的豎直向加速度響應信號的時間曲線圖。 (a) 3號節點 (b) 6號節點 (c) 9號節點圖5 節點加速度響應Fig.5 Node of acceleration response 采用DATA-SSI算法識別出該簡支梁在第1分鐘內的穩定圖,如圖6所示。根據圖6可知,其中的第1階真實模態(3.4 Hz左右)的穩定軸很清晰,第2階真實模態(12.7 Hz左右)則被隱藏在虛假模態中,第三階模態(27.1 Hz左右)也被隱藏在虛假模態中。 圖6 穩定圖1Fig.6 Stability diagram 1 基于第3章步驟2的算法步驟,可確定合理的單次信號窗口時間長度在25 s,則可將10 min的信號分為24個連續窗口。采用DATA-SSI算法識別出各窗口振動信號的穩定圖,圖7為第1個窗口對應的穩定圖。對比分析圖6和圖7可知,對信號輸入長度進行合理的窗口劃分能夠在一定程度上剔除虛假模態,保留真實模態。 圖7 穩定圖2Fig.7 Stabilization diagram 2 基于第3章中所提的步驟4~步驟7完成對本簡支梁在10 min內共24個窗口信號(24幅穩定圖)的密度聚類,并求解各聚類模態的平均值繪制到圖8所示聚類穩定圖中。對比圖6、圖7和圖8可知,本文所提算法能精確地識別出橋梁結構的真實模態。 圖8 穩定圖3Fig.8 Stability diagram 3 為驗證圖2所示ICDATA-SSI模態參數智能化識別算法能夠運用于實際橋梁結構的參數識別中,現以三峽大壩壩址上游一處大型斜拉橋為識別對象,其橋跨布置為149.00 m+330.00 m+149.00 m,其中主跨和邊跨長度分別為330.00 m和149.00 m,橋面總寬度18.00 m,兩側均設置1.50 m寬的人行道。 該斜拉橋主梁上共設置11處加速度傳感器,用于采集主梁在環境作用或列車作用的豎向加速度振動信號,對應的信號采用頻率為20 Hz,即每一秒采集20次數據。圖9為該斜拉橋的1/2橋型布置圖,圖中編號J1~J6為橋上加速度傳感器的具體布置位置。圖10為該斜拉橋在環境激勵下隨機提取到的連續200 s內的豎向加速度響應信號,縱坐標代表加速度數值。 圖9 橋跨布置圖(m)Fig.9 Layout of bridge span (m) 圖10 振動信號時程圖Fig.10 Time-distance chart of vibration signal 該斜拉橋索塔總高115.00 m呈倒Y型,橋面以上高度為82.40 m。涉及的主要材料包括鋼筋混凝土和鋼材,其中鋼筋混凝土結構的彈性模量為2.06×105N/mm2,泊松比為0.17;鋼材的彈性模量為3.43×104N/mm2,泊松比為0.30。全橋共涉及1 104個節點和1 028個單位,在圖9中①和②的點均設置橋墩,墩底均按固結處理;橋梁的兩端均放開順橋向的約束以保證橋梁的正常伸縮。 該橋MIDAS設計模型如圖11所示。基于MIDAS軟件自帶的特征值分析識別該斜拉橋的各階豎向彎曲模態振型圖,圖12給為前四階模態振型圖。 圖11 三維有限元模型(MIDAS)Fig.11 Finite element model of three-dimensional (MIDAS) (b) 二階豎向彎曲振型 (c) 三階豎向彎曲振型 (d) 四階豎向彎曲振型圖12 前三階模態振型圖(MIDAS)Fig.12 Modal shape of the first three orders (MIDAS) 為進一步驗證MIDAS軟件所得模態參數結果具有可靠性,相關檢測單位對該斜拉橋進行了動力特性測試,具體試驗項目包括跑車、剎車、跳車、脈動等。試驗所采用的車輛相關參數如表1所示。該車型為雙軸車,車輛根據前后軸質量不同分為5種工況。以下簡要論述跳車試驗的實現步驟和參數識別結果,具體如下: 表1 車輛相關參數表Tab.1 The relevant parameters of the vehicle (1) 確定測試截面位置 共對三個截面進行測試,分別為圖9中的截面J3、J5和J6。 (2) 布置每個截面的測試點 按照圖13所示測點位置,在每個截面上布置動應變測點和加速度測點。 注:“”為動應變測點;“”為振動加速度測點。圖13 測點布置圖(cm)Fig.13 Layout of monitoring points (cm) (3) 采集結構振動信號 分別在三個截面位置采用五種工況的“車輛荷載”進行跳車試驗以使主梁產生一定的振動,并通過布置在截面上的“振動加速度傳感器”采集振動信號,最后對信號進行分析計算識別出主梁的自振頻率。對比五種不同車輛荷載工況下的結構自振頻率,結果表明該主梁結構的固有頻率值受車輛荷載的影響很小,圖14為“加載編號B5”情況下的信號頻譜分析結果,圖15為對應的跳車自振頻譜圖。 圖14 信號頻譜分析結果Fig.14 Frequency spectrum of fluctuating signal 圖15 實測跳車自振頻譜圖Fig.15 Measured natural vibration spectrum for stagger 以下將簡要介紹如何將ICDATA-SSI算法運用于智能化識別該斜拉橋的模態參數,具體實現步驟如下: 步驟1:采集振動信號 通過事先布置在主梁上的11處加速度傳感器采集該斜拉橋在任意一天24 h內對應的振動信號,并保存為信號矩陣X=[i,j],其中i代表具體的信號點數,即i=1,2,…,1 728 000,j代表傳感器個數,即j=1,2,…,11。 步驟2:確定窗口大小和滑窗步長 基于第3章步驟2的算法步驟,確定單個窗口大小為20 min,即每個窗口的輸入信號矩陣為24 000×11,24 000代表20 min采集到的振動信號個數,11代表傳感器總數。滑窗步長為單個窗口的一半長度,對應12 000個測點數。 步驟3:各窗口模態參數識別結果 采用DATA-SSI算法識別各窗口振動信號的穩定圖,圖16為任意四個窗口對應的穩定圖。由圖16可知,結構的真實模態是以相似或者相同的方式不斷重復出現,而虛假模態則出現隨機性。 (a) 穩定圖4(時間:01:00—01:20) (b) 穩定圖5(時間:01:20—01:40) (c) 穩定圖6(時間:01:40—02:00) (d) 穩定圖7(時間:02:00—02:20)圖16 穩定圖Fig.16 Stability diagram 步驟4:確定鄰域半徑和密度閾值 在采用DATA-SSI算法和OPTICS算法對各窗口的振動信號進行模態參數識別和密度聚類時,需分別采用式(6)、式(13)和式(15)計算各自對應的密度閾值、頻率鄰域半徑和模態振型鄰域半徑。 步驟5:最終的聚類穩定圖 基于第3章所提的步驟4~步驟7完成對本斜拉橋在一天24 h內共72個窗口信號(72幅穩定圖)的密度聚類,并求解各聚類模態的平均值繪制到圖11所示聚類穩定圖中。 為進一步驗證ICDATA-SSI算法智能識別所得固有頻率值具有可靠性,現將圖17中所得前9階自振頻率值與5.2節的MIDAS特征值分析結果,與5.3節該斜拉橋的動力特性實測結果進行差值百分比分析,結果如表2所示,對比分析各結果間的差值百分比可知,本文結果與動力特性實測結果在前9階頻率值間的差值百分比范圍為[-4.34%,3.40%];與理論值結果間的差值百分比范圍為[-4.62%,4.84%];與理論值和實際值的平均值間的差值百分比范圍為[-4.09%,3.7%]。 圖17 聚類穩定圖Fig.17 Clustering stability diagram 表2 頻率值對比分析表Tab.2 Comparative analysis table of frequency values 綜合上述可知:本文所提ICDATA-SSI算法識別的結果與理論值(MIDAS有限元結果)以及實際值(現場動力特性實測結果)間的誤差均在5%以內,可見本文算法所得結果具有可靠性,能夠運用于識別實際橋梁結構的頻率值。 結合第3章步驟4中第2)步所提“模態振型聚類”實現步驟,可知頻率值和模態振型應具有相同的聚類屬性,即模態頻率值屬于同類,則模態振型也應屬于同類。于此,為進一步驗證本文所提算法能識別出該斜拉橋的真實模態振型圖,得到圖18所示前三階二維模態振型圖和圖19所示前三階三維模態振型圖。圖18和圖19中橫坐標的數值從1~11,代表主梁上共設置的11處傳感器,縱坐標為各點對應的歸一化處理后的振型幅值。通過將這兩幅模態振型圖與圖12所示MIDAS識別的模態振型圖(理論值)進行對比分析,可知本文所提算法識別所得前三階模態振型圖與理論振型圖具有95%以上的相似性,即表明本文算法可以運用于識別實際橋梁結構的模態振型,且識別結果具有可靠性。 (a) 一階模態振型 (b) 二階模態振型 (c) 三階模態振型圖18 二維模態振型圖Fig.18 Modal shape (two-dimensional diagram) (a) 一階模態振型 (b) 二階模態振型 (c) 三階模態振型圖19 三維模態振型圖Fig.19 Modal shape (three-dimensional diagram) 本文通過引入滑窗機制和密度聚類算法來克服SSI算法無法實現穩定圖中真假模態的自動篩選,并將其運用于識別簡支梁模擬試驗和某實際大型斜拉橋的頻率和模態振型。結果表明: (1) 本文所提滑窗原理能實現對輸入信號的合理劃分,能避免因單次輸入信號過多引起的虛假模態,單次輸入信號過少導致的真實模態遺漏現象。 (2) 密度聚類算法相比分層聚類和劃分聚類算法具有一定的優勢,主要表現在該算法不因輸入數據的增多而降低聚類效果,初始輸入參數最少,對數據的順序無要求,能處理高維度的數據。 (3) 運用OPTICS聚類算法中的鄰域半徑和密度閾值能實現對穩定圖中的模態參數的密度聚類。 (4) 識別所得某大型斜拉橋主梁的頻率值結果與理論值(MIDAS有限元結果)以及實際值(現場動力特性實測結果)間的誤差均在5%以內,且識別的模態振型圖與MIDAS軟件識別的模態振型圖具有很高的相似性。 綜上可知,本文所提基于滑窗技術和OPTICS密度聚類算法的改進DATA-SSI模態參數智能識別算法具有可靠性。1.2 參數設定

1.3 聚類流程


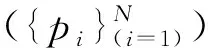
2 信號合理劃分
2.1 滑窗算法選擇
2.2 窗口大小確定
2.3 窗口滑動步長

3 改進DATA-SSI算法










4 模擬試驗


4.1 環境激勵模擬

4.2 振動響應信號



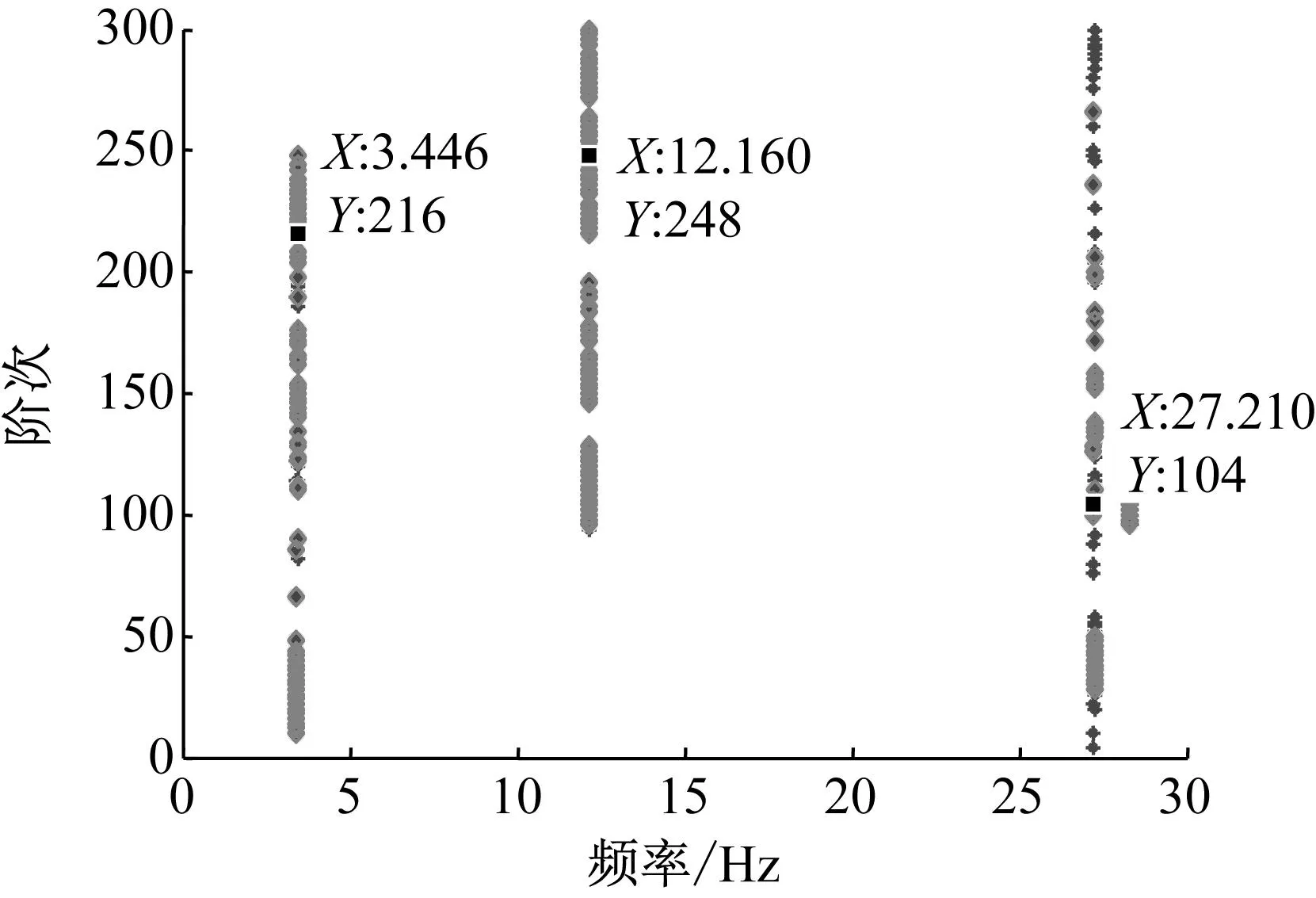
4.3 穩定圖識別


5 實際工程算例
5.1 工程概況

5.2 有限元計算結果



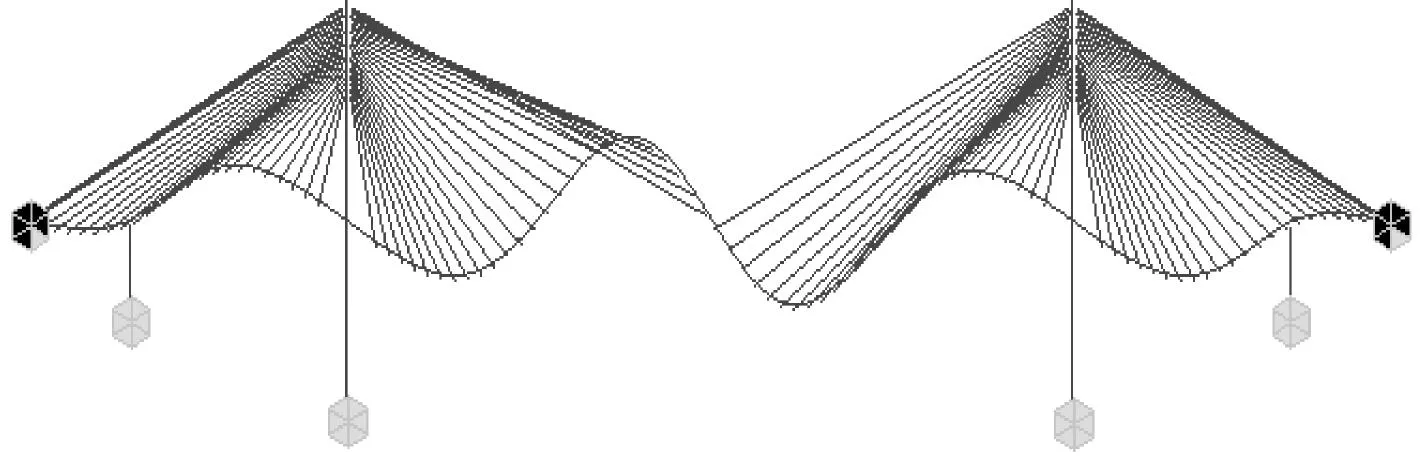
5.3 動力特性實測結果




5.4 自振頻率結果






5.5 模態振型結果

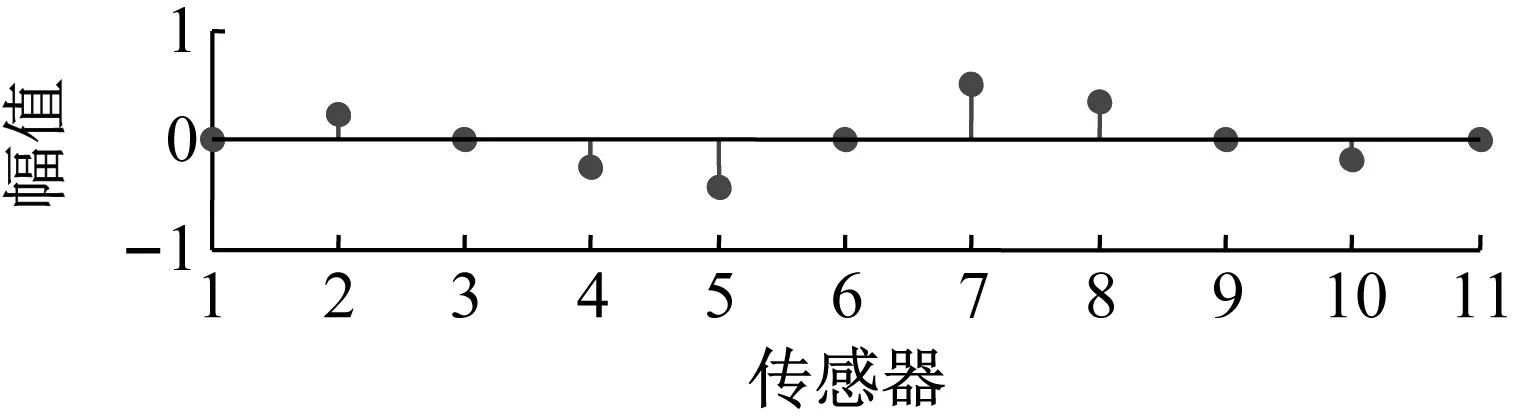

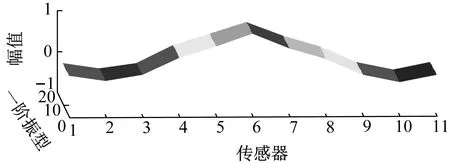


6 結 論

