基于廣義條件強度參數的水平和豎向地震動聯合選取研究

2024-04-20 11:26:36王曉磊王浠銘閻衛東呂大剛

振動與沖擊 2024年7期

王曉磊, 王浠銘, 閻衛東, 呂大剛

(1.沈陽建筑大學土木工程學院,沈陽 110168; 2.哈爾濱工業大學土木工程學院,哈爾濱 150090)

工程抗震領域早期認為,地震作用下建筑結構的損傷主要是由于水平向地震動引起的。然而隨著抗震設計標準的提高與高烈度地震災害的出現,研究人員開始重視豎向地震動對結構的影響[1]。目前我國對豎向地震作用的考慮主要采用GB 50011—2010 《建筑抗震設計規范》中5.1.1節第四條規定:“豎向地震動影響系數的最大值可取水平向地震動影響系數最大值的65%”,然而在一些高震級地震事件中[2-7],豎向與水平向地震作用的比值超過了“65%”這個數值,甚至豎向地震作用超過水平向。因此,仍然以“65%”來考慮豎向地震作用可能有些保守。另外,豎向地震作用也可能對特定的工程結構造成較大影響,例如大壩[8]、公路橋梁[9-10]、冷卻塔[11]和核電站[12]等。如何合理地考慮豎向地震動是目前工程抗震分析與結構安全性評價中關鍵問題之一。

在地震反應分析中,輸入合理的地震動是考慮地震作用最有效的方法之一,因此如何科學地選取輸入地震動成為近年來工程抗震領域主要關注的問題之一。目前地震動選取方法主要分為基于地震學參數選取、基于最不利地震動選取和基于地震動強度參數選取等[13],其中,基于地震動強度參數選取是目前較為主流的選取方法,該方法主要匹配目標包括一致危險譜(uniform hazard spectrum, UHS)、條件均值譜/條件譜(conditional mean spectrum, CMS/conditional spectrum, CS)[14]和廣義條件強度參數(generalized conditional intensity measure, GCIM)[15]。早期廣泛采用的是基于UHS選取方法,但UHS中不同周期Sa(T)是由不同設定地震控制的,并且與單個地震事件之間存在差異,選取結果偏于保守;針對這一問題,Baker提出了基于CMS地震動選取方法,該譜是以特定周期Sa(T)作為條件,考慮不同周期Sa(T)之間的相關性來構建目標譜。然而上述地震動選取方法僅考慮了以Sa(T)表征的地震動特性,地震動的破壞性還取決于頻譜、振幅、累積效應、持時等方面,因此,在此基礎上,Bradley提出一種能夠以任意地震動強度參數(intensity measure, IM)為目標的整體選取方法GCIM[16]。GCIM理論是以某一IM作為條件,利用IM間相關性,構建目標IM的條件分布,然后對實際地震動進行匹配來完成選取[17]。GCIM方法可認為是CMS/CS的擴展,即將目標反應譜更換為IM條件分布來進行地震動匹配。上述方法旨在根據一個或多個感興趣的 IM來選擇最能代表控制場地地震活動的記錄。

上述選取方法已廣泛應用于水平向地震動選取中,而針對豎向地震動選取的研究相對發展緩慢。目前,豎向地震動的選取方法主要包括以下三種:①直接選用與水平向選取結果相對應的豎向地震動記錄;②直接采用豎向地震動預測方程(ground motion prediction equation, GMPE)構建豎向目標譜;③基于水平目標譜,結合V/H模型生成豎向目標譜進行選取。由于第一種方法只關注了水平向地震動,因此可能會導致豎向地震動出現“失真”的情況;第二種方法會導致分解出的水平和豎向地震場景可能存在稍微不同[18];第三種方法雖然考慮了水平與豎向地震動譜加速度之間的關系,但是該方法的局限性在于:在地震學參數(例如震級、斷層距和場地條件等)方面,豎向地震動的比例可能不同于水平向,V/H模型很難解釋這些差異和標準差[19]。

值得注意的是,無論是采用豎向GMPE還是V/H模型,這些構造目標譜的方法都忽略了豎向IM之間的相關性。因此,能夠考慮IM間相關性的CMS/CS方法被擴展到豎向地震動選取中。Gülerce等[20]提出了基于V/H模型構建豎向CMS的方法,該方法采用V/H模型對水平CMS進行縮放或者在此基礎上考慮了V/H-水平相關性來構建豎向CMS。另外,目前豎向地震動的選取方法中都沒有同時考慮水平和豎向地震動其他特性(如振幅、累積效應、持時等方面)。而且,上述地震動選取方法通常僅致力于單向目標譜的生成,雖然有些方法同時生成了水平和豎向CMS,但在選取過程中仍然采用分別匹配(獨立進行)的形式選取水平和豎向地震動,即先后分別選取符合各自目標譜的水平和豎向地震動。目前,水平和豎向地震動聯合選取方法主要包括:①基于水平目標譜選取水平地震動記錄,然后選取相應的豎向地震動記錄[21];②基于豎向目標譜選取豎向地震動記錄,然后選取相應的水平向地震動記錄。由于水平和豎向地震動為一組地震動的不同分量,其作用機理方面聯系密切,忽略其相關關系會導致選取出現誤差,但目前還未有研究學者提出考慮強度參數相關性的水平和豎向地震動聯合選取方法。

綜上,雖然采用CMS/CS選取方法能夠較好體現目標場地的地震危險性,但多數研究將其應用在單向或水平兩向地震動選取中,僅有少量研究[22]提出了水平和豎向地震動向量型CS的聯合選取方法,但該選取方法中沒有考慮到除反應譜以外的IM。隨著近年來對結構抗震性能要求的提高,豎向地震動IM的重要性逐漸增加。例如,豎向地震動在短周期內產生較大的結構響應,一些短周期結構可能對豎向高頻IMs敏感(例如,加速度譜強度ASI)[23];在對海域結構進行抗震分析時,豎向PGD作為海域長周期地震動強度參數更為合理[24];此外,一些豎向IM被證明是在工程需求參數分析和概率地震需求分析中的最佳IM[25-27]。因此,將GCIM理論拓展至豎向地震動領域中可以考慮多個表征不同特性的豎向IM,進而選取出符合預期目標的地震動數據。基于GCIM理論的水平和豎向地震動聯合選取方法能夠有效克服現有研究方法不足,為工程結構的三向反應分析奠定基礎。

本研究對GCIM的基本理論進行拓展,提出水平和豎向地震動GCIM分布的構建方法,并與“無條件分布”對比。另外,提出基于GCIM的水平和豎向地震動聯合選取理論方法,給出以水平IM作為條件的實際算例,利用水平-豎向IM相關系數模型構建水平和豎向地震動GCIM目標分布,將選取結果與傳統選取方法進行對比,說明該方法的合理性。

1 水平和豎向地震動GCIM分布構建

GCIM的理論基礎與CMS一致,即假設任意數量的地震動參數集IM={IM1,IM2,IM3,…,IMn}服從多元對數正態分布,上述IM可以為任意周期的Sa(T),或者能夠表征地震動其他特性的IM(如ASI、VSI、DSI、SI、EPA、EPV、EPD、CAV、AI、PGA、PGV、Ds575、Ds575等)。

目前,基于GCIM的地震動選取方法僅被應用于水平向地震動選取中,然而,為了合理地選取豎向地震動,在選取過程中應當考慮豎向地震動的特性,因此,將GCIM選取理論應用于豎向地震動的挑選具有重要的研究意義與應用價值。此外,由于水平和豎向地震動之間的關系較為密切,應對水平和豎向地震動進行聯合選取研究。

1.1 GCIM基本原理

概率地震危險性分析(probabilistic seismic hazard analysis, PSHA)已成為目前評估地震危險性最常用的方法,也是基于GCIM條件分布來選取地震動過程中必要的環節。一般地,PSHA可給出某場地條件下,某一強度參數IMj的年發生率

(1)

式中,λIMj(imj)為IMj>imj時的年發生率;PIMj|Rup(imj|rupk)為給定地震破裂情景Rup=rupk下IMj>imj的概率;λRup(rupk)是地震破裂情景Rup=rupk的年發生率;NRup是可能發生的地震破裂情景(假定彼此獨立)的數量。

對于IMj>imj,利用貝葉斯定理對PSHA結果進行解耦,可以確定當地震破裂情景Rup=rupk時的條件概率

PRup|IMj(rupk|IMj≥imj)=

(2)

通過全概率定理,即可得到給定IMj=imj時,由地震破裂情景Rup=rupk引起的條件概率

PRup|IMj(rupk|IMj=imj)≈

PRup|IMj(rupk|IMj≥imj+Δimj)λIMj(imj+Δimj)]

(3)

對于NRup個地震破裂情形,PRup|IMj(rupk|imj)就形成了一個互斥的集合,因此對于給定IMj=imj下,IMi的條件概率密度函數fIMi|IMj(imi|imj)為

fIMi|IMj(imi|imj)=

(4)

fIMi|Rup,IMj(imi|rupk,imj)～

(5)

式中,μln IMi|Rup,IMj和σln IMi|Rup,IMj是該對數正態分布的均值和標準差,可分別表示為

μln IMi|Rup,IMj(rupk,imj)=

μln IMi|Rup(rupk)+σln IMi|Rup(rupk)ρln IMi,ln IMj|Rupεln IMj

(6)

(7)

式中,μln IMi|Rup(rupk)和σln IMi|Rup(rupk)可由GMPE求解得到,ρln IMi,ln IMj|Rup為lnIMi和lnIMj之間的相關系數,εln IMj計算公式可表示為

(8)

1.2 水平和豎向地震動GCIM分布構建方法

本文1.1節中詳細闡述了基于GCIM進行地震動選取時目標分布的構建過程,為了實現水平和豎向地震動聯合選取,基于水平和豎向IM之間的相關系數模型,提出了水平和豎向地震動GCIM條件分布的構建方法。

從GCIM的基本原理可以看出,GCIM理論的關鍵步驟就是基于GMPE和穩健的相關系數模型構建出準確的目標IM條件分布,即計算出生成條件分布所需的IM條件均值和對數標準差(即式(6)和(7)),因此為了構建水平和豎向GCIM的條件分布,需要計算出水平和豎向目標IM的條件均值和對數標準差,可分別表示為

μln IMV,i|Rup,IMH,j(rupk,imH,j)=μln IMV,i|Rup(rupk)+
σln IMV,i|Rup(rupk)ρln IMV,i,ln IMH,j|Rupεln IMH,j

(9)

(10)

式中:μln IMV,i|Rup(rupk)和σln IMV,i|Rup(rupk)分別為基于rupk地震破裂情景下,豎向GMPE輸出的目標IM對數均值以及對數標準差;ρln IMV,i,ln IMH,j|Rup為水平和豎向IM間的相關系數,可從相關系數模型中獲得;εln IMH,j為水平IM的標準化總殘差。需要說明的是,上述條件均值和對數標準差計算公式是以水平向IM作為條件來進行說明,但對于不同的水平和豎向地震動分析需求時,可選擇任意方向IM作為條件。基于上述方法就可以獲得多個水平和豎向目標IM的條件分布,從而實現水平和豎向地震動的聯合選取。

1.3 水平和豎向地震動IM相關系數模型

地震動IM之間的相關性是構建GCIM條件分布的關鍵步驟,一般可從IM相關系數模型中獲得。IM相關系數模型的建立步驟主要包括:①基于特定地震動數據,結合GMPE預測出IM的中位值和對數標準差;②計算IM的標準化殘差;③利用標準化殘差代替IM計算相關系數;④建立相關系數參數化預測模型。

對于水平和豎向地震動GCIM分布的構建,需要采用針對水平和豎向地震動IM建立的相關系數模型,模型的穩健性與全面性決定了構建出目標分布是否準確。現有研究中提出的水平和豎向IM相關系數模型較少,表1中列出了目前可用的幾種相關系數模型及其理論細節。表1中:BC06模型[28]是最早提出的水平-豎向強度參數之間的相關系數模型,由Baker等基于NGA-West1數據庫和AS1997 GMPE觀察得到,包含SaH(V)(0.05 s～5 s);KPBV20模型[29]由Kohrangi等提出,基于NGA-West2數據庫和兩組水平和豎向GMPE研究了Sa(0.01～10 s)、PGA、PGV、Ds575和Ds595之間的經驗相關性;Wang等提出了WW23模型[30],該模型基于NGA-West2數據庫和CB14&BC16 GMPE,包含的IM范圍更加廣泛(見表1);另外,Wang等又提出WZ23模型[31],與WW23模型不同的是,該模型著重關注于水平和豎向Sa(T)之間的相關性。

表1 水平-豎向IM相關系數模型Tab.1 H-V IM correlation coefficient models

2 基于GCIM的水平和豎向地震動記錄聯合選取

2.1 GCIM選取理論

本文1.2節闡述了GCIM條件分布的構造方法,在此基礎上,根據目標IM的條件分布對備選數據庫進行匹配從而實現地震動選取。與基于CMS選取地震動不同,在進行地震動匹配時,GCIM理論首先需要模擬出與目標分布等效的多元對數正態分布(即具有相同的均值向量和標準差向量以及相關結構),均值和標準差向量分別可表示為

μln IM|Rup,IMj=
{μln IM1|Rup,IMj,μln IM2|Rup,IMj,…,μln IMn|Rup,IMj}

(11)

σln IM|Rup,IMj=
{σln IM1|Rup,IMj,σln IM2|Rup,IMj,…,σln IMn|Rup,IMj}

(12)

式中,相關結構可從本文建立的相關系數模型中獲取。

由于GCIM方法涵蓋的地震動IM較多,不同IM之間的物理意義、量級等方面可能存在一定差異,為了在匹配地震動時合理地考慮這種差異,需要將實際IM值與目標值之間的差值除以其標準差來進行標準化處理。另外,在面對不同的抗震分析需求時,對每個IM的關注程度也不同,需要在選取過程中應當對IM賦予不同的權重。綜上所述,能夠合理考慮以上不確定性的指標rm,nism可表示為

(13)

與其他地震動選取方法不同,GCIM方法采用了地震動記錄集合IM的經驗累積分布與理論分布相匹配的方式,本文采用K-S檢驗來衡量經驗分布與理論分布之間的差異,重復多次匹配過程計算R值,最后選取R值最小的地震動記錄集合作為最優結果

(14)

(15)

2.2 基于GCIM的水平和豎向地震動聯合選取方法

目前針對豎向地震動的選取方法幾乎無法同時考慮豎向地震動頻譜以外其他特性,并且很難保證選取結果中水平和豎向地震動同時符合預期目標且是同一組地震動的不同分量。因此,本文為了克服上述選取方法的不足,提出了基于GCIM理論的水平和豎向地震動聯合選取方法。

為了實現水平和豎向地震動的聯合選取(選取出地震動記錄來自同一地震事件),本文將水平和豎向地震動進行組合,通常情況下,一條單向地震動記錄能計算出一組IM信息,即IM={IM1,IM2,IM3,…,IMn},同一地震事件的水平和豎向地震動可以得到兩組分別包含水平和豎向的IM信息,將兩組IM信息進行組合,得到該地震事件的全部IM信息組,即IM={IMH,1,IMH,2,IMH,3,…,IMH,n,IMV,1,IMV,2,IMV,3,…,IMV,m},如圖1所示。然后,將該IM信息組與目標分布進行匹配就能實現水平和豎向地震動記錄的聯合選取。采用這種方法能夠選取出一組地震動記錄,分別為兩條水平和一條豎向地震動,該方法保證了選取的地震動來自同一地震事件。盡管GCIM理論能夠自定義目標IM的數量,但是由于聯合選取時的IM信息組分別包含水平和豎向IM,目標IM的數量會增多,這可能會加大地震動匹配難度,并且水平和豎向地震動特性之間的不確定性也會導致選取出的地震動記錄減少或者出現所選地震動記錄集合的經驗分布與理論分布不完全匹配的情況,可能的解決辦法就是合理的分配權重wi,或者減少地震動選取數量。

圖1 水平和豎向地震動記錄所包含的IM信息示意圖Fig.1 Schematic diagram of IM information contained in horizontal and vertical ground motion records

對此本文提出一種基于GCIM的水平和豎向地震動聯合選取方法,具體步驟如圖2所示,主要包括以下步驟:

圖2 基于GCIM的水平和豎向地震動聯合選取方法步驟Fig.2 The steps of GCIM-based joint horizontal and vertical ground motion selection method

(1) 確定初始條件:給出水平和豎向地震動選取的危險性水平和場地信息,選取條件IM與目標參數集IMH,V;

(2) PSHA分析:對上述初始條件進行PSHA分析,得到某超越概率下,條件IM的危險性曲線;

(3) 獲取設定地震信息:對條件IM的危險性曲線進行解耦得到NRup個地震破裂情景,計算平均設定地震事件;

(4) 構造水平和豎向IM條件分布:基于設定地震信息,根據式(9)和(10),采用水平和豎向IM的GMPE和相關系數模型構建目標參數集IMH,V的條件分布;

(5) 模擬多元對數正態分布:基于目標參數集IMH,V的條件均值和標準差向量,模擬出等效的水平和豎向IM多元對數正態分布;

(6) 匹配水平和豎向地震動:首先確定需要循環的次數n;其次從備選數據庫中隨機選取地震動子集,計算目標參數集IMH,V的調幅因子,基于模擬多元對數正態分布,計算指標rm,nism與R值;最后從n次循環中選取最優結果,得到水平和豎向地震動記錄。

3 算例分析

3.1 水平和豎向地震動聯合選取算例

基于上述方法,本節給出了基于GCIM的水平和豎向地震動聯合選取實際算例。由于在地震動選取程序中,多數是以水平向為主,因此本算例以水平地震動IM作為條件,其余水平和豎向地震動IM為目標。但如果豎向地震動占主導地位,也可以將豎向IM作為條件。本算例將危險性水平設定為50年內超越概率為10%,以SaH(T=1.0 s)作為條件IM,以地震動強度參數集IMH,V={SaH(0.05 s),SaH(0.1 s),SaH(0.2 s),SaH(0.3 s),SaH(0.5 s),SaH(2.0 s),SaH(5.0 s),SaH(10.0 s),Ds595,CAVH,AIH,PGVH,SaV(0.05 s),SaV(0.1 s),SaV(0.2 s),SaV(0.3 s),SaV(0.5 s),SaV(2.0 s),ASIV,SIV,EPAV,PGAV}作為目標,對水平和豎向地震動IM的條件分布進行構建。對于上述水平和豎向IM,本算例采用的GMPE如表2所示。

表2 所考慮IM的GMPETab.2 The GMPE of the IMs considered

對于IM相關系數模型,本算例分別采用Wang等提出的水平-水平[38]、水平-豎向IM相關系數模型。此外,本算例還采用了1996 USGS地震破裂預測模型[39],通過OpenSHA軟件[40]獲得位于California巖石場地(緯度=34.053,經度=118.243,VS30=760 m/s)SaH(T=1.0 s)的地震危險性曲線,然后對該危險性曲線進行解耦,得到了該超越概率下可能導致地震危險的設定地震信息,結果如圖3所示。

(a) SaH(T=1.0 s)的危險性曲線

(b) 50年內超越概率10%的SaH(T=1.0 s)危險性解耦圖3 SaH(T=1.0 s)的危險性曲線與解耦Fig.3 Seismic hazard curve and disaggregation for SaH(T=1.0 s)

基于上述解耦的設定地震信息,將計算出目標參數集IMH,V的條件分布和“無條件”分布(僅使用GMPE計算得到均值和標準差直接生成,過程中忽略IM間相關性)進行對比,對比結果如圖4和圖5所示。可發現:CSH和CSV均大于“無條件”分布,并且隨著周期的增加,差異逐漸減小;目標參數集IMH,V的條件分布也不同于“無條件”分布,并且隨著相關系數的降低,這種差異可能會變小,例如,SaH(1.0 s)與SaH(0.1 s)之間的相關系數較小(ρ=0.04),但SaH(0.1 s)條件分布和無條件分布相似;相反,SaH(1.0 s)與PGVH之間的高度相關(ρ=0.84),其條件分布和無條件分布則存在顯著不同。

圖4 水平向地震動IM的條件分布Fig.4 Conditional distributions of horizontal ground motion IMs

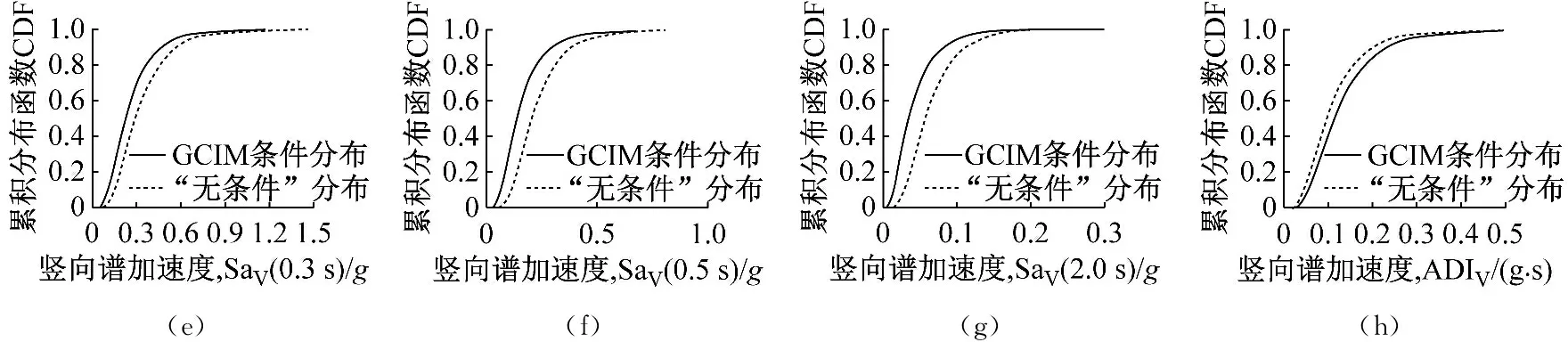
圖5 豎向地震動IM的條件分布Fig.5 Conditional distributions of vertical ground motion IMs

上述現象表明:直接采用GMPE來進行地震動選取與實際情況不符,考慮水平和豎向IM之間的相關性來構建水平和豎向地震動目標譜是有意義的。另外,本節選擇的IM只是本算例的范圍,可以根據工程抗震實際需求選擇任意IM進行地震動選取。

基于上述水平和豎向IM目標參數集的條件分布,采用2.2節提出的聯合選取方法對地震動目標數據庫中地震動進行匹配。本節將NGA-West2數據庫作為目標數據庫,該數據庫包含21 539組地震動記錄,其中某些地震動記錄缺少豎向分量,另外編號RSN4577-4839、RSN8055-9194的地震動記錄不能從PEER網站上檢索到。因此,將上述地震動記錄排除后,最后目標數據庫共包含16 429組地震動記錄。

基于上述準備工作對水平和豎向地震動進行聯合選取,為了說明考慮豎向地震動IM后選取方法的合理性,本節還展示了僅考慮水平地震動IM的選取結果,并將其與聯合選取結果進行對比。

基于水平和豎向GCIM目標條件分布的聯合選取結果共計30組地震動,本文將選取結果與理論分布和KS邊界之間進行對比,結果如圖6所示。可發現:

圖6 基于水平和豎向GCIM的地震動選取結果Fig.6 The results of ground motion selection based on horizontal and vertical GCIM

(1) 在顯著性水平為10%的情況下,所選取地震動記錄集的每個目標IM經驗累積分布與理論分布匹配良好,雖然極個別目標IM存在輕微觸界的情況,但是也都通過了KS檢驗,接受了原假設。

(2) 每個目標IM被分配了不同的權重,其中Ds595、CAVH、AIH、PGVH分別被分配0.1的權重系數,不同振動周期的SaH(T)、SaV(T)均分其余的0.6權重系數。但是ASIV、SIV、EPAV、PGAV并沒有分配權重系數,這是因為本文考慮了短、中周期的SaV(T),而這4個IM與這些周期的SaV(T)表現出良好的相關性,因此本文將權重系數分配給其他目標IM以達到最優選取效果。此外本文為了簡便,對其他目標IM采取了均分權重的分配形式。在實際應用中,可以根據對不同地震動特性的關注程度和實際選取過程來調整權重系數。

本節還將聯合選取結果的水平與豎向反應譜與CSH(V)進行對比,結果如圖7所示。可以看出,所選記錄集的水平和豎向反應譜多數與CSH(V)匹配良好,相應中值反應譜也較為吻合,僅有少部分記錄處于±2σ范圍以外,這可能是因為本GCIM算例雖然考慮了Sa(T),但僅選取了16個振動周期Sa(T)作為目標IM,而GCIM本質上是綜合考慮不同地震動特性的方法,因此從反應譜角度來說,該選取效果沒有以CS譜為目標譜的選取方法效果好。但本文認為圖7中的對比結果也能夠表明GCIM方法在考慮其他特性IM后,仍然能夠較好地體現頻譜特性。

(a) 水平向地震動記錄

(b) 豎向地震動記錄圖7 地震動聯合選取結果的水平和豎向反應譜與CSH(V)對比Fig.7 The comparison of horizontal and vertical response spectra with CSH(V) for joint selection results of ground motion

所選地震動記錄集的震級MW和斷層距Rrup分布情況見圖8(a)所示,可以看出,所選地震動記錄的震級MW和斷層距Rrup大多分布在6～7級和2～100 km區間里,震級均值μMW斷層距均值μRrup分別為6.5級和35 km。另外,選取過程中22個目標IM調幅系數的經驗累積分布如圖8(b)所示。能夠看出,多數目標IM的調幅系數沒有超過5,不會出現由于調幅過大而造成地震動記錄失真的情況。

(a) 選取結果的震級和斷層距分布

(b) 調幅系數分布圖8 選取結果的震級、斷層距和調幅系數分布Fig.8 The magnitude-distance and amplitude scale factors distribution of the selected ground motions

3.2 選取結果比較

為了與基于水平和豎向GCIM聯合選取結果對比,本節僅考慮水平向GCIM對地震動進行選取,豎向直接采用與水平向選取結果相對應的豎向地震動記錄,目標參數為IMH,V中的12個水平IM,即IMH={SaH(0.05 s),SaH(0.1 s),SaH(0.2 s),SaH(0.3 s),SaH(0.5 s),SaH(2.0 s),SaH(5.0 s),SaH(10.0 s),Ds595,CAVH,AIH,PGVH},僅基于水平向GCIM的地震動選取結果共計30組地震動記錄,選取結果的累積經驗分布與理論分布之間的比較如圖9所示。可以看出,與3.1節的選取結果類似,基于水平向IM所選取地震動記錄集的經驗累積分布與理論分布也匹配良好。

圖9 基于水平向GCIM的地震動選取結果Fig.9 The results of ground motion selection based on horizontal GCIM

另外,該次選取結果的震級、斷層距和目標IM調幅系數的分布如圖10所示。震級均值μMW斷層距均值μRrup分別為6.5級和29 km,調幅系數依舊不超過5,這與3.1節的情況相似。

(a) 選取結果的震級和斷層距分布

(b) 調幅系數分布圖10 選取結果的震級、斷層距和調幅系數分布Fig.10 The magnitude-distance and amplitude scale factors distribution of the selected ground motions

本節將僅基于水平向GCIM選取結果的豎向地震動記錄集的目標IM(共計10個)經驗累積分布與3.1節中聯合選取結果及其理論分布進行比較,對比結果如圖11所示。由圖11可知:僅基于水平向GCIM選取結果的所有豎向目標IM均超出KS界線(顯著性水平為10%),這表示均未通過KS檢驗;雖然SaV(0.05 s)與理論分布匹配相對于其他IM較好,但是也發生了觸界現象;另外,基于水平和豎向GCIM選取結果的豎向目標IM經驗累積分布與該豎向數據集也相差較大,這意味著“僅考慮水平GCIM對地震動進行選取,豎向地震動采用與結果相對應”的通用做法缺少對豎向地震動特性的考慮,會造成豎向地震動不符合預期的后果;值得注意的是,兩次選取結果的震級和斷層距分布較為相似,均值也十分接近,這意味著考慮了豎向GCIM的地震動選取并不會對水平向造成影響,并且能夠更加合理地、全面地對水平和豎向地震動進行聯合分析。

圖11 兩次選取結果的豎向IM對比Fig.11 The comparison of vertical IM of the two selection results

4 結論

本章提出了基于水平和豎向GCIM的地震動聯合選取方法,構建了水平和豎向GCIM的目標分布,從目標數據庫中挑選出與之匹配的三向地震動記錄,并且與僅考慮水平向GCIM的選取結果進行對比,主要研究結論如下:

(1) 基于水平和豎向IM相關系數模型構建的目標IM分布與“無條件”分布之間存在一定差異,這種差異的變化與相關系數有關,隨著相關系數的降低,差異可能會變小,表明考慮水平和豎向IM之間的相關性來構建水平和豎向地震動目標譜是更加符合實際的。

(2) 基于水平和豎向GCIM聯合選取出的三向地震動記錄與目標理論分布匹配良好,所選地震動記錄集的震級均值μMW斷層距均值μRrup與解耦出的平均目標設定地震差別不大。

(3) 與僅考慮水平向GCIM地震動選取方法對比發現,基于水平和豎向GCIM的聯合選取方法能夠很好地考慮到豎向地震動特性,并且聯合選取方法不會對水平向造成影響,在其基礎上更加合理地、全面地對水平和豎向地震動進行聯合分析。