基于改進麻雀搜索算法的變電構架優化方法
張迎春, 姜 嵐, 唐 波, 陳 曦, 胡 輝
(1.三峽大學 電氣與新能源學院,湖北 宜昌 443002; 2.湖北省輸電線路工程技術研究中心,湖北 宜昌 443002;3.國網湖北省電力有限公司經濟技術研究院,武漢 430000; 4.智方設計股份有限公司,武漢 430000)
近年來,隨著新型電力系統概念的提出,輸變電工程結構的安全性與可靠性也被廣泛關注。由于供電需求的逐步提升與輸變電技術的不斷發展,高壓、特高壓輸電工程已經成為電網建設的重點。變電站構架是輸變電工程中非常重要的工程結構,主要承受導線張力和各種環境荷載。隨著電壓等級的提升,變電構架承受的荷載更復雜,結構高度、跨度的提高導致用鋼量也越來越大。因此,在保證結構穩定性與安全性的前提下,能夠通過優化設計減少鋼材用量,使得結構更加經濟與環保具有重要意義。
將變電構架的三角形格構式梁視為空間桁架結構進行優化分析,目前,桁架結構的優化類型主要分為尺寸優化、形狀優化、拓撲優化三種[1-2],所涉及的優化方法主要有最優準則法、數學規劃法以及智能優化方法三大類[3-4]。其中,最優準則法對于單約束的優化問題更加有效,難以適應多種形態的約束;數學規劃法是一種精確的求解方法,但對于多變量大型復雜結構的優化設計,其計算量過大,通用性差;而智能優化算法近年來發展迅速,遺傳算法、粒子群算法、鯨魚優化算法等被相繼提出,因該類算法有著魯棒性強、通用性好且易于與其他算法相結合等優點[5-6],所以其在結構優化設計方面有著較為廣泛的應用。麻雀搜索算法(sparrow search algorithm, SSA)由Xue等[7]于2020年提出,作為一種新型群體智能優化算法,它的優化思想主要來源于麻雀種群的覓食行為和反捕食行為。該算法能夠處理連續型以及離散型設計變量,且無需計算靈敏度,對約束條件也沒有特殊要求。根據其在測試函數中的結果表明,與粒子群算法、灰狼優化算法等相比,該算法的魯棒性更強,收斂速度更快,有望在結構優化領域發揮重要作用。
本文在基本麻雀搜索算法的基礎上加入Circle混沌映射以及螢火蟲擾動策略,對其易陷入局部最優解,收斂速度慢[8]等缺點進行改進,而后建立桁架結構的尺寸優化模型,并將改進麻雀搜索算法(improved sparrow search algorithm, ISSA)用于典型桁架結構以及變電構架的尺寸優化研究,結果表明了該算法在結構優化設計中的有效性。
1 麻雀搜索算法及改進
1.1 麻雀搜索算法
根據麻雀群體的覓食行為及反捕食行為,可以將麻雀種群抽象為探索者-跟隨者-預警者模型。其中,探索者在種群中的能量儲備最高,具有較好的適應度值,它們為整個種群提供覓食的方向;跟隨者會密切關注探索者,從而獲得更好的食物來源,以增加自身的適應度值;預警者會在遇到危險時發出警報,此時,處于種群邊緣的麻雀會移動到安全區域,處于中間位置的麻雀則會隨機游走,靠近其他麻雀[9]。
將SSA用于優化問題,若在D維搜索空間中存在著N只麻雀,則第i只麻雀在空間中的位置為Xi=[xi1,…,xid,…,xiD],相對應的適應度值為Fx=[f(xi1),…,f(xid),…,f(xiD)],其中,i=1,2,…,N,表示種群中的麻雀個數;d=1,2,…,D,表示待優化問題的設計變量維數。
在SSA中,探索者有著更廣泛的搜索范圍,因此會在搜索過程中優先獲得食物來源,在每次的迭代過程中,探索者的位置更新描述如下
(1)
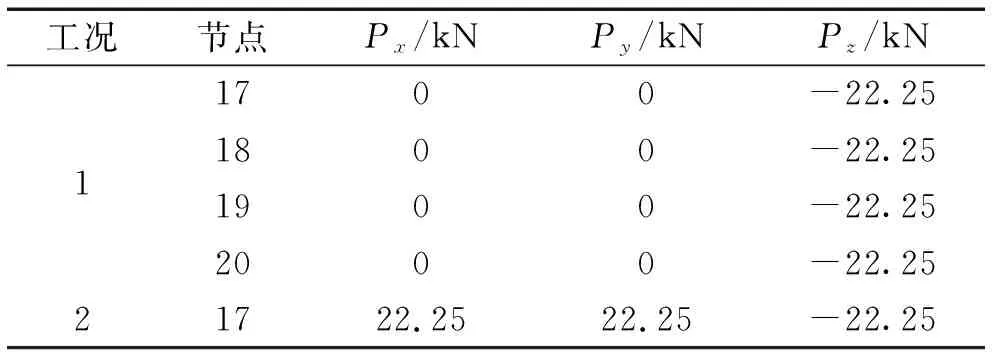
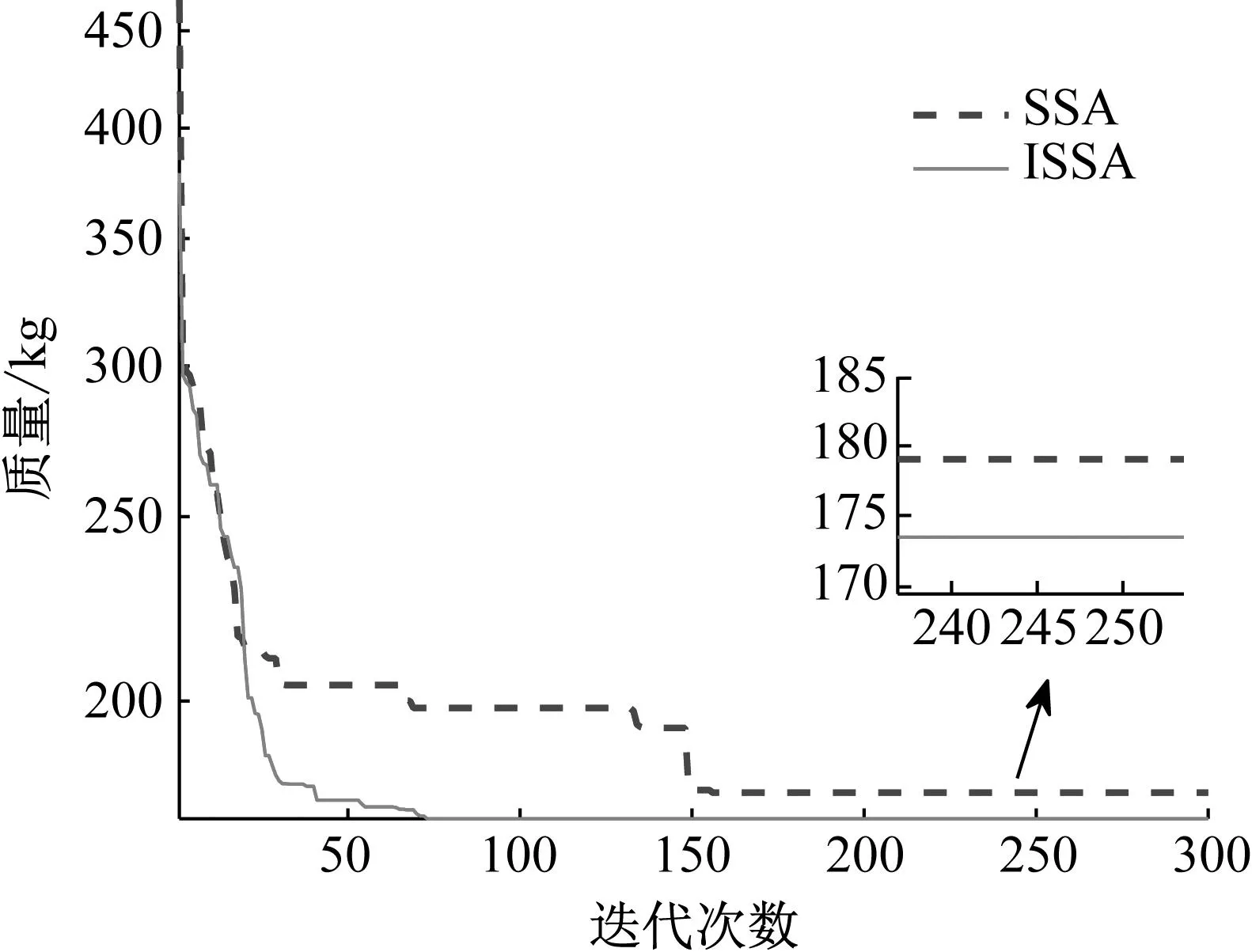
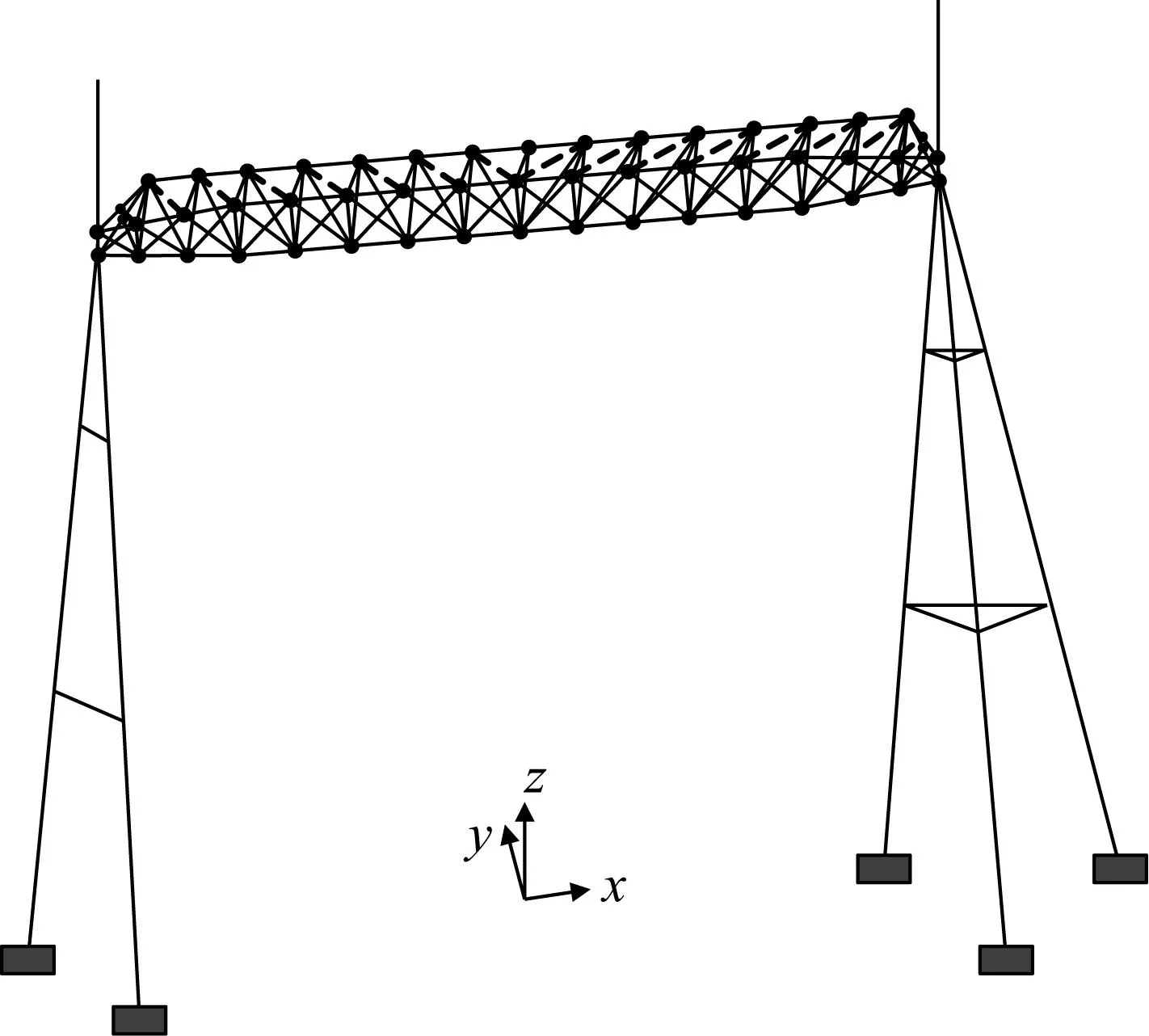
式中:t為當前的迭代次數;itermax為最大的迭代次數;α∈(0,1]隨機取值;Q為服從正態分布的隨機數;L為元素全為1的1×d矩陣;R2∈[0,1]為預警值;ST∈[0.5,1]為安全值。當R2 種群中除了探索者以外,其余麻雀均為跟隨者,迭代過程中,跟隨者的位置更新描述如下 (2) 式中:xworst為當前種群中的全局最差位置;xp為當前發現者的最優位置;A+=AT(AAT)-1,A為1×d矩陣,矩陣中的每個元素被隨機賦值為1或-1。當i>N/2時,表明第i個跟隨者沒有獲得食物,適應度值較低,需迫切飛往他處覓食;當i≤N/2時,表明第i個跟隨者將在最優位置附近覓食。 在種群中隨機挑選麻雀作為預警者,其數量一般占種群的10%~20%,預警者的位置更新描述如下 (3) 式中:xbest為當前全局的最優位置;β為步長控制參數,服從正態分布(均值為0,方差為1);K∈[-1,1]隨機取值;fi、fw、fg分別為當前麻雀個體適應度值、當前全局最差適應度值及最佳適應度值;ε為防止分母為零的極小常數。當fi>fg時,表明麻雀處于種群邊緣,易被捕食者攻擊;當fi=fg時,表示處于種群中間位置的麻雀意識到了危險,需向其他麻雀靠近以躲避攻擊。 針對基本麻雀搜索算法在優化時易陷入局部極值,收斂速度慢等缺點,對其進行改進。因混沌作為一種普遍存在的非線性現象,具有遍歷性、隨機性等特點[10-11],所以在原算法的基礎上加入Circle混沌映射,使算法的初始值分布更加均勻,增加種群的多樣性,提升算法的收斂性;為避免SSA陷入局部最優解,對所有麻雀更新后的位置進行螢火蟲擾動,以提高其尋優精度。 1.2.1 Circle混沌映射 由于基本麻雀搜索算法在生成初始種群時具有隨機性,所以會出現聚集等分布不均的情況,使得其在整個解空間中的覆蓋率不高,不利于算法的廣泛搜索,所以許多學者會引入混沌映射來解決此類問題。鑒于Circle混沌映射的覆蓋率較高且比較穩定,所以本文在初始種群生成時采用Circle混沌映射以增加種群的多樣性,使其分布更加均勻。 Circle混沌映射的表達式如下 (4) 式中:i+1表示解的維度數。當維度為500時,Circle混沌映射初始解的維度分布圖與直方圖分別如圖1和圖2所示。由圖1和2可知,Circle映射的混沌值在[0,1]之間的分布較均勻。 圖1 Circle混沌映射分布圖Fig.1 Circle chaotic map distribution 圖2 Circle混沌映射直方圖Fig.2 Circle chaotic map histogram 1.2.2 螢火蟲擾動策略 螢火蟲算法(firefly algorithm, FA)是由Yang[12]于2008年提出的一種元啟發式算法。螢火蟲主要通過發光來實現求偶或者覓食的目的,因此該算法模擬了螢火蟲的發光特性,將搜索與優化過程模擬為螢火蟲的吸引與移動過程。本文針對基本麻雀搜索算法易陷入局部最優的問題,在算法最后引入了螢火蟲擾動策略,對麻雀個體的位置進行擾動更新,將擾動后的適應度值與擾動前的值進行對比,若適應度值更優,則進行位置更新。螢火蟲的吸引度描述如下 (5) 式中:β0為最大吸引度;γ為光強吸收系數;ri,j為螢火蟲i與j之間的距離。 螢火蟲i被螢火蟲j吸引并向其移動的位置更新描述如下 xi=xi+β*(xj-xi)+α*(rand-1/2) (6) 式中:xi和xj分別為螢火蟲i和j所處的空間位置;α∈[0,1]為步長因子。 本文對于變電構架梁的尺寸優化設計,主要以結構質量最輕為目標函數,以桿件的橫截面積為設計變量,且取離散值,以桿件的應力,長細比以及節點的位移為約束條件,由此建立的優化設計數學模型描述如下。 以結構質量最輕建立的目標函數為 (7) 式中:W為結構的總質量;Ai∈S為桿件的截面面積;S={S1,S2,…,SNS}為可選用的桿件截面離散集;ρi與li分別為第i根桿件的材料密度和單元長度;n為結構中的桿件數量。 考慮的約束條件主要如下: (1) 桿件的應力約束 (8) (2) 桿件的長細比約束 (9) (3) 節點的位移約束 uj-[u]≤0 (10) 式中:σi為第i根桿件的應力;f為鋼材的強度設計值;φi為軸心受壓構件的穩定系數;λi為第i根桿件的長細比;[λ]C與[λ]T分別為桿件受壓以及受拉的許用長細比;uj為第j個節點的位移值;[u]為節點的許用位移值。 對于變電構架梁的優化設計,屬于有約束的優化問題,相比于無約束優化,有約束優化使得可行域變小,搜索空間也更加復雜,因此會增大求解難度。對于有約束的優化問題,目前主要有罰函數法、可行性法則、隨機排序法等約束處理方法,其中罰函數法是最為常用的處理方法之一[13-15],在求最小值的優化問題中,其原理可簡單解釋為,對不滿足約束條件的解賦予一個較大的值,故在尋找最小值的優化過程中,此解將會被排除在外。本文將采用罰函數法來處理桿件的應力,長細比以及節點的位移這些約束條件,此方法是對原來的目標函數增加懲罰項,從而將約束優化問題轉換為無約束優化問題來處理,故最終建立的目標函數如下所示 (11) 在對桁架結構進行優化設計時,主要采用有限單元法作為結構分析方法。有限元法主要分為離散化、單元分析以及整體分析三部分,對于桁架結構,可將桿件視為單元,在MATLAB中編制桁架結構的內力分析程序,可求得單元剛度矩陣、結構的整體剛度矩陣,進而得出節點位移以及單元內力等結果,用于分析判斷是否滿足約束條件。 結合尺寸優化設計的數學模型,采用改進麻雀搜索算法進行尺寸優化設計的流程如圖3所示。 圖3 尺寸優化設計流程Fig.3 Size optimization design process 為方便與其他優化算法進行對比分析,算例選用兩種廣泛用于結構優化設計,以驗證各優化算法是否有效的空間桁架結構,即25桿及72桿空間桁架結構。其中,前者形似輸電鐵塔結構,共10個節點,25根桿件;后者為四層塔架結構,共20個節點,72根桿件。分別將改進前后的算法用于兩種桁架結構的尺寸優化分析。 25桿空間桁架結構的節點編號及尺寸信息如圖4所示。結構中桿件的彈性模量E=6.895×1010Pa,密度ρ=2 768.8 kg/m3,許用應力為2.759×108Pa,節點在x、y、z方向上的許用位移為0.889 cm。本例將桁架結構的25根桿件分為8組,分組信息如表1所示,結構的荷載工況如表2所示,桿件截面的離散集S如表3所示。 圖4 25桿空間桁架(cm)Fig.4 25 bar space truss (cm) 表1 結構桿件連接及分組Tab.1 Connection and grouping of structural members 表2 荷載工況Tab.2 Load case 表3 桿件截面離散集Tab.3 Discrete set of member section 72桿空間桁架結構的節點編號及尺寸信息如圖5所示。其中,L=152.4 cm。結構中桿件的彈性模量E=6.895×1010Pa,許用應力為1.724×108Pa,密度ρ=2 768.8 kg/m3,結構頂部四個節點在x、y、z方向上的許用位移為0.635 cm。根據對稱性,將桁架結構的72根桿件分為16組,分組號如表4所示,結構的荷載工況如表5所示,桿件截面的離散集S見表3。 圖5 72桿空間桁架Fig.5 72 bar space truss 表4 桿件分組Tab.4 Bar grouping 表5 荷載工況Tab.5 Load case 將SSA與ISSA分別用于25桿及72桿空間桁架結構的尺寸優化設計,其中,算法所涉及的參數值設置如下:種群數量N=50,最大迭代次數itermax(25桿)=200,itermax(72桿)=300,探索者占種群數量的20%,其余為跟隨者,預警者占種群數量的20%,安全值ST=0.8,最大吸引度β0=1,光強吸收系數γ=1,步長因子α=0.2。 將基本麻雀搜索算法及改進麻雀搜索算法分別獨立運行20次,并將結果與現有文獻進行對比。兩種空間桁架結構的優化結果分別如表6和表7所示,算法改進前后的收斂曲線分別如圖6和圖7所示。 表6 25桿空間桁架優化結果Tab.6 Optimization results of 25 bar space truss 表7 72桿空間桁架優化結果Tab.7 Optimization results of 72 bar space truss 圖7 72桿空間桁架優化收斂曲線Fig.7 Convergence curve of 72 bar space truss optimization 對于25桿空間桁架結構的尺寸優化,由表6可知,ISSA的最優值與文獻[16-18]相比雖只減少了約0.1%,但其平均值及標準差明顯小于其他文獻算法,表明ISSA更加穩定,魯棒性更強,這主要由于加入了螢火蟲擾動策略,使算法易于跳出局部極值,具有更強的穩定性。ISSA的最優值與SSA相比雖相差不大,但同樣其平均值及標準差明顯更小,且由圖6可知,改進后的算法迭代不到30次就找到了最優解,而基本麻雀搜索算法迭代將近50次才趨于收斂,可見,改進后的算法收斂速度更快,這主要由于加入了Circle混沌映射,使得初始值分布更加均勻,增加了其靠近最優解的概率,以至提升了算法的收斂速度。 對于72桿空間桁架結構的尺寸優化,由表7結果可知,ISSA的最優值相比于文獻[19-21]及SSA的最優值,分別減少了8.8%、0.9%、0.2%及3.1%。與SSA相比,ISSA有著更小的平均值及標準差。其中,與文獻[21]相比,ISSA的優化效果雖不明顯,但文獻[21]中所提算法在優化時迭代將近200次才得到最優解,而由圖7可知,ISSA迭代70次左右就找到了最優解,可見,ISSA的收斂速度明顯更快。 將改進麻雀搜索算法用于某500 kV變電構架梁的尺寸優化設計,其中,變電構架高26 m,構架梁為三相掛點,跨度為27 m,地線柱高8 m,構架梁上下弦桿均采用鋼管,其余構件采用角鋼,橫梁高為2 m,寬為1.8 m,到端部變為1.1 m,變電構架整體模型如圖8所示。構架采用Q235鋼,鋼材的強度設計值f=2.15×108Pa,還應考慮相應的折減系數,具體參考DL/T 5457—2012 《變電站建筑結構設計技術規程》[22],彈性模量E=2.06×1011Pa,質量密度ρ=7 850 kg/m3。構架梁跨中的撓度限值為梁總跨度的1/300,橫梁上下弦桿及立面支座角鋼的許用長細比為150,其余桿件的許用長細比為200。 圖8 變電構架模型Fig.8 Model of substation structure 將構架梁中的桿件分為7組,具體分組信息在展開式構架梁中表示,如圖9所示。 圖9 桿件分組(mm)Fig.9 Bar grouping (mm) 桿件截面離散集S={L40×4(3.09 cm2),L45×4(3.49 cm2),L40×5(3.79 cm2),L50×4(3.9 cm2),L56×4(4.39 cm2),L50×5(4.8 cm2),L56×5(5.42 cm2),L63×5(6.14 cm2),L70×5(6.88 cm2),L63×6(7.29 cm2),L75×5(7.41 cm2),L80×5(7.91 cm2),L70×6(8.16 cm2),L75×6(8.8 cm2),L80×6(9.4 cm2),L75×7(10.16 cm2),L90×6(10.64 cm2),L80×7(10.86 cm2),L90×7(12.3 cm2),L90×8(13.94 cm2),Φ146×5(22.15 cm2),Φ152×5(23.09 cm2),Φ159×5(24.19 cm2),Φ152×5.5(25.31 cm2),Φ146×6(26.39 cm2)},其中,前20個用于角鋼選型,其余用于鋼管選型。 此變電構架主要考慮最嚴重覆冰、最大風速、最低氣溫、單相上人、三相上人以及單相緊線六種工況,但由變電構架的資料可知,最低氣溫、三相上人和單相緊線三種工況下的荷載組合不起控制作用,所以在受力分析時主要考慮另外三種工況下的荷載組合。所分析的荷載主要包括:結構自重、風荷載(順導線方向以及垂直導線方向)、導線張力,其中,最大風速工況下,風速v=28 m/s,最嚴重覆冰及單相上人工況下,風速v=10 m/s,垂直于結構表面的風荷載標準值計算公式如下 Wk=βzμsμzW0 (12) 式中:Wk為風荷載標準值(kN/m2);βz為高度z處的風振系數;μs為風荷載體型系數;μz為風壓高度變化系數;W0為基本風壓(kN/m2)。 在三種工況下對變電構架梁進行優化設計,其中,算法最大迭代次數itermax=300,其余算法參數設置同算例分析。優化結果及收斂曲線分別如表8和圖10所示。 表8 變電構架梁優化結果Tab.8 Optimization results of substation structure beam 圖10 構架梁優化收斂曲線Fig.10 Optimization convergence curve of structure beam 由以上結果可知,采用改進麻雀搜索算法對變電構架梁進行尺寸優化設計,優化率約為15.5%。當取得最優值時,結構中桿件所受最大拉應力為159 MPa,最大壓應力為-126 MPa,均小于許用應力值;結構中弦桿及立面支座角鋼的最大長細比為137,小于150,其余桿件的最大長細比為192,小于200;構架梁跨中的最大位移值為0.026 m,小于許用位移值。由此可知,改進后算法能夠在保證結構穩定性與安全性的前提下,提高其經濟性。 本文主要對基本麻雀搜索算法做出改進,并建立了桁架結構的尺寸優化模型,結合結構分析的有限元法,將改進麻雀搜索算法分別用于經典桁架結構以及變電構架的尺寸優化設計,得到的主要結論如下: (1) 針對麻雀搜索算法易陷入局部最優及收斂速度慢的缺點進行改進,分別引入Circle混沌映射及螢火蟲擾動,增強了算法的魯棒性,提升了算法的收斂速度。 (2) 改進麻雀搜索算法在算例分析中,與文獻及基本麻雀搜索算法相比,其優化效果均有提升,穩定性及收斂速度明顯提高。 (3) 將改進麻雀搜索算法用于實際工程中變電構架梁的優化設計,改進后算法對于變電構架梁的優化率約為15%,表明其適用于工程中的初步設計階段,具有實用價值。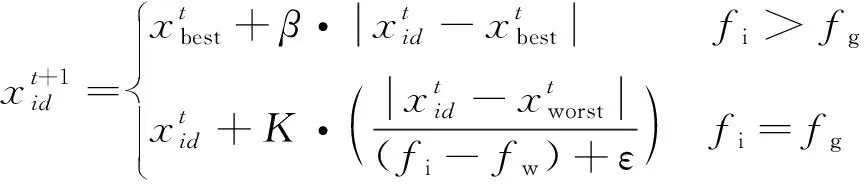
1.2 改進麻雀搜索算法


2 尺寸優化模型及優化流程
2.1 尺寸優化模型


2.2 優化流程

3 算例分析
3.1 25桿空間桁架結構




3.2 72桿空間桁架結構





4 工程應用



5 結 論

