保持架兜孔形狀對(duì)高速角接觸球軸承保持架動(dòng)態(tài)性能的影響分析

陳世金, 鄒冬良, 王亞坤, 蔡?hào)|明

(五冶集團(tuán)上海有限公司,上海 201900)

高速角接觸球軸承廣泛應(yīng)用于航空發(fā)動(dòng)機(jī)主軸、航天慣性?xún)x表、新能源汽車(chē)主軸以及高速精密機(jī)床主軸等高速轉(zhuǎn)子系統(tǒng)中,軸承性能以及壽命往往決定著系統(tǒng)能否正常運(yùn)行,而保持架的動(dòng)態(tài)特性是保證高速球軸承性能的關(guān)鍵。保持架不穩(wěn)定運(yùn)動(dòng)不僅會(huì)使軸承力矩波動(dòng),產(chǎn)生嘯叫聲,還會(huì)加劇保持架磨損,甚至使其斷裂,從而引起軸承精度喪失或使軸承卡死造成災(zāi)難性后果[1]。Kingsbury[2]第一次通過(guò)試驗(yàn)發(fā)現(xiàn)了保持架不穩(wěn)定運(yùn)動(dòng)與軸承力矩波動(dòng)之間的關(guān)系,認(rèn)為軸承鋼球與保持架兜孔之間的摩擦力驅(qū)動(dòng)保持架渦動(dòng),保持架的不穩(wěn)定渦動(dòng)導(dǎo)致軸承摩擦力矩波動(dòng)并產(chǎn)生嘯叫聲。Walters[3]最早建立了球4自由度、保持架6自由度的球軸承動(dòng)力學(xué)模型,奠定了滾動(dòng)軸承保持架動(dòng)力學(xué)分析的基礎(chǔ)。Gupta[4-8]建立了所有零件具有6自由度的滾動(dòng)軸承完全動(dòng)力學(xué)模型,可以模擬時(shí)變工況下軸承零件的瞬態(tài)運(yùn)動(dòng)特性,并系統(tǒng)分析了工況、潤(rùn)滑、摩擦以及幾何等因素對(duì)保持架穩(wěn)定性的影響。國(guó)內(nèi)基于滾動(dòng)軸承動(dòng)力學(xué)模型的保持架動(dòng)態(tài)特性研究近10年有了較快發(fā)展,Liu等[9-14]以Gupta動(dòng)力學(xué)模型為基礎(chǔ)針對(duì)各自工況進(jìn)行一定簡(jiǎn)化,對(duì)保持架的動(dòng)態(tài)性能分析提供了諸多有益探討。分析指出,保持架兜孔間隙和引導(dǎo)間隙等是影響保持架動(dòng)力學(xué)性能的重要參數(shù),然而上述學(xué)者大多針對(duì)的是單一的圓柱形兜孔保持架,保持架兜孔形狀作為對(duì)保持架結(jié)構(gòu)影響更大的參數(shù)反而未被深入探究。此外,由于動(dòng)力學(xué)模型較復(fù)雜,國(guó)內(nèi)學(xué)者大多采用集成較多內(nèi)部函數(shù)的Matlab語(yǔ)言進(jìn)行程序開(kāi)發(fā),以降低程序開(kāi)發(fā)難度,但是由于Matlab語(yǔ)言計(jì)算效率較低,程序運(yùn)行耗時(shí)非常長(zhǎng),給出的結(jié)果中保持架甚至未進(jìn)入穩(wěn)定運(yùn)行階段(仿真軸承運(yùn)行時(shí)間不到0.1 s)。Sathyan等[15]通過(guò)試驗(yàn)探究發(fā)現(xiàn)方形兜孔保持架摩擦力矩的穩(wěn)定性數(shù)倍優(yōu)于圓柱形兜孔保持架。鄧四二等[16]利用能量守恒定律,建立角接觸球軸承摩擦力矩理論計(jì)算公式,發(fā)現(xiàn)低速時(shí)方形兜孔保持架有利于軸承摩擦力矩的降低,反之則是圓柱形更有利。Yan等[17]建立了球6自由度、內(nèi)圈5自由度和保持架3自由度的球軸承擬動(dòng)力學(xué)模型,分析了球兜孔和圓柱兜孔對(duì)軸承溫度的影響,結(jié)果表明球形兜孔保持架更利于軸承的散熱。

綜上所述,眾多學(xué)者對(duì)保持架動(dòng)力學(xué)特性探究做了諸多探索,但主要集中在工況、潤(rùn)滑、摩擦、兜孔間隙和引導(dǎo)間隙等方面,對(duì)保持架結(jié)構(gòu)影響非常大的兜孔形狀則較少涉及。而工程人員發(fā)現(xiàn)在某軸承中采用圓柱兜孔保持架時(shí)會(huì)產(chǎn)生嘯叫聲,而改換成方形兜孔保持架后嘯叫聲會(huì)減弱甚至消失。Sathyan等和鄧四二等的研究表明兜孔形狀對(duì)軸承摩擦力矩以及散熱有較大影響,但由于未建立完全動(dòng)力學(xué)模型,缺乏對(duì)保持架的動(dòng)力學(xué)特性分析,且僅對(duì)某兩種兜孔形狀進(jìn)行探討,缺乏對(duì)不同保持架兜孔形狀的綜合討論。陳世金等[18]試驗(yàn)探究了不同兜孔形狀對(duì)軸承保持架質(zhì)心軌跡和打滑率的影響規(guī)律,發(fā)現(xiàn)兜孔形狀對(duì)保持架運(yùn)動(dòng)影響顯著,但對(duì)其內(nèi)在作用機(jī)理缺乏足夠分析。本文在上述試驗(yàn)研究工作的基礎(chǔ)上,以高速角接觸球軸承為研究對(duì)象,分別建立方柱形(方形)兜孔、圓柱形(圓形)兜孔以及球形兜孔保持架的球軸承動(dòng)力學(xué)數(shù)值仿真模型,并采用Fortran語(yǔ)言進(jìn)行程序開(kāi)發(fā),大幅提高計(jì)算效率,分析軸承運(yùn)行2 s內(nèi)不同兜孔形狀以及間隙比對(duì)保持架運(yùn)動(dòng)、受力以及磨損的影響,探究兜孔形狀對(duì)保持架運(yùn)動(dòng)的作用機(jī)理,并以試驗(yàn)分別對(duì)三種兜孔保持架的動(dòng)力學(xué)模型加以驗(yàn)證。

1 模型建立

本文基于課題組建立的高速儀表轉(zhuǎn)子軸承動(dòng)力學(xué)磨損數(shù)值仿真模型,建立了方形、圓柱形和球形保持架動(dòng)力學(xué)模型,球和不同兜孔形狀保持架的相互作用及保持架與引導(dǎo)套圈的相互作用介紹如下,球和內(nèi)外圈的相互作用可以參考Zhang等。

1.1 坐標(biāo)系與變換

假定軸承各零件幾何中心與質(zhì)心重合,軸承各坐標(biāo)系中心建立在零件幾何中心上,各零件的質(zhì)心運(yùn)動(dòng)在慣性坐標(biāo)系中描述,繞質(zhì)心的轉(zhuǎn)動(dòng)在其定體坐標(biāo)系。軸承各零件坐標(biāo)系的定義如圖1所示。

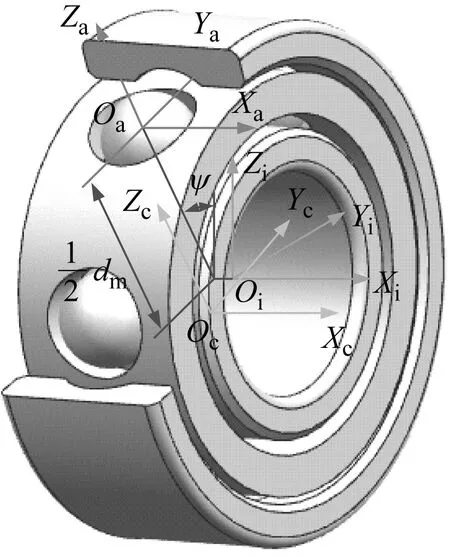
圖1 軸承各零件坐標(biāo)系定義Fig.1 Definition of coordinate system

從一個(gè)坐標(biāo)系到另一個(gè)坐標(biāo)系的轉(zhuǎn)換可以通過(guò)三次相繼的旋轉(zhuǎn)實(shí)現(xiàn),轉(zhuǎn)換矩陣是

(1)

零件在定體坐標(biāo)系中的角速度與三次旋轉(zhuǎn)的角度(η,ξ,λ)之間的關(guān)系為[19]

(2)

式中,(ω1,ω2,ω3)為軸承零件在定體坐標(biāo)系中的角速度分量。

1.2 保持架的運(yùn)動(dòng)方程

保持架在空間中共有6個(gè)自由度,分別為保持架的質(zhì)心運(yùn)動(dòng)以及保持架的旋轉(zhuǎn)運(yùn)動(dòng),保持架在三維空間的質(zhì)心運(yùn)動(dòng)可以在慣性坐標(biāo)系中描述

(3)

式中:mc為保持架的質(zhì)量;xc,yc和zc為保持架在慣性坐標(biāo)系中的位置;Fcx,Fcy和Fcz分別為保持架所受的總力在x,y和z方向的分量。

保持架的旋轉(zhuǎn)運(yùn)動(dòng)(動(dòng)量矩方程)可以在其定體坐標(biāo)系中描述

(4)

式中:mc為保持架的質(zhì)量;Ic1,Ic2,Ic3為保持架轉(zhuǎn)動(dòng)慣量;ωc1,ωc2,ωc3為保持架的角速度在不同方向的分量;Mc1,Mc2,Mc3為作用于保持架的合力矩在不同方向的分量。

根據(jù)擬靜力學(xué)結(jié)果給定保持架的初始位置和速度,采用變步長(zhǎng)的四階Runge-Kutta法對(duì)上述微分方程求解,即可得到保持架在任意時(shí)刻的位置、速度、載荷以及磨損率等。下面將介紹保持架與球以及引導(dǎo)套圈的相互作用,以得到保持架的所受的合力和合力矩。

1.3 保持架球與的相互作用

圖2(a)～(c)分別為方形兜孔、圓形兜孔和球形兜孔保持架的結(jié)構(gòu)示意圖。由于保持架與球形兜孔保持架的計(jì)算最為復(fù)雜,本文以球與球形兜孔保持架的相互作用為例進(jìn)行介紹。

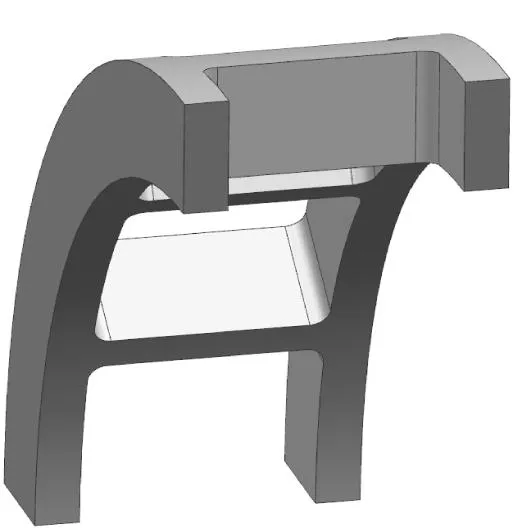
(a) 方形兜孔

(b) 圓形兜孔

(c) 球形兜孔圖2 不同形狀兜孔保持架結(jié)構(gòu)圖Fig.2 Structural diagram of pocket cages with different shapes

如圖3所示,慣性坐標(biāo)系中,球心相對(duì)保持架中心的位置向量為

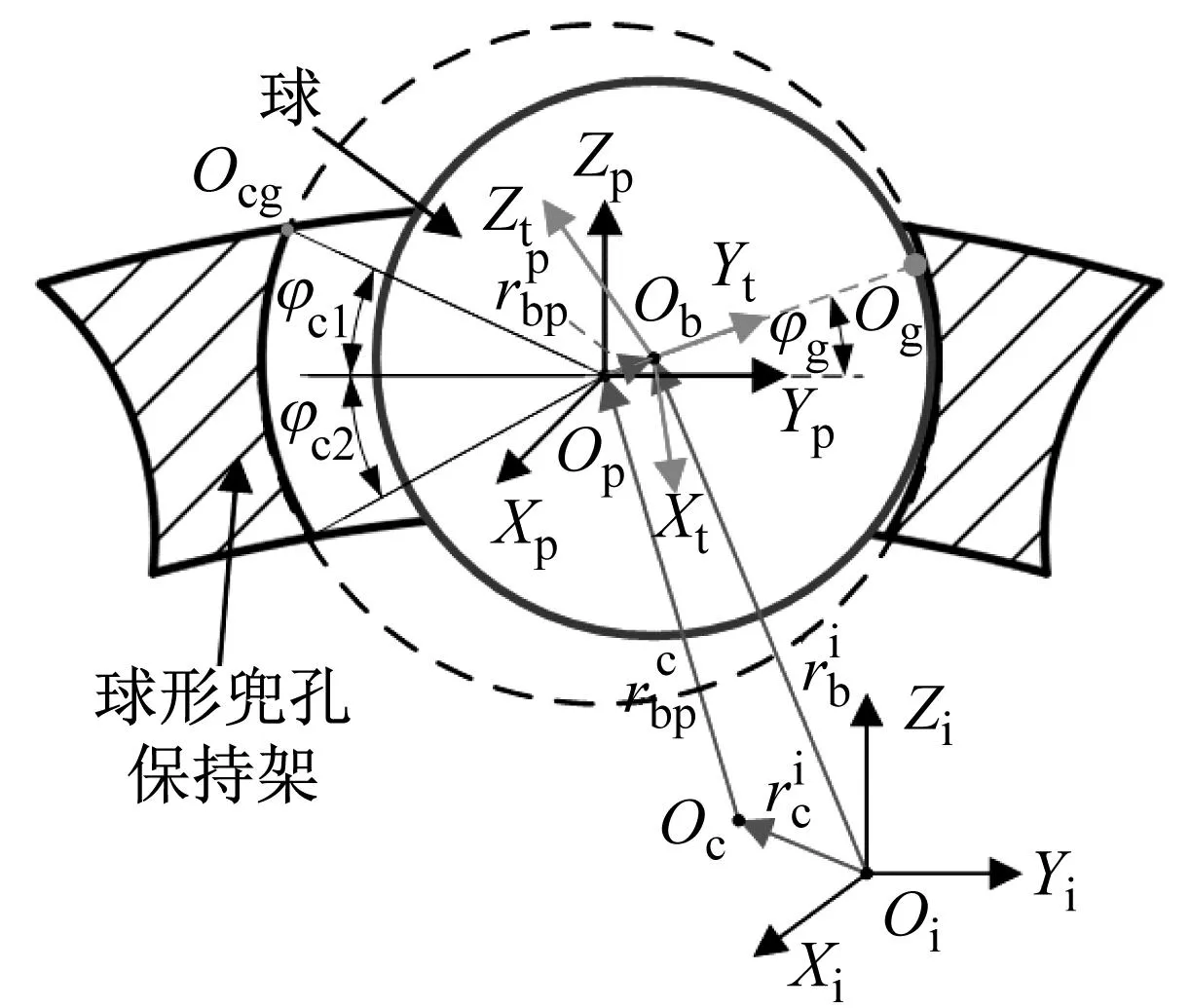
(a) 碰撞點(diǎn)在兜孔球面

(b) 碰撞點(diǎn)在兜孔邊界圖3 球與球兜孔保持架的相互作用Fig.3 Interaction between ball and spherical pocket cage

(5)

(6)

式中,Tic=T(φc1,φc2,φc3)為從慣性坐標(biāo)系到保持架坐標(biāo)系的轉(zhuǎn)換矩陣,φc1,φc2和φc3為保持架的姿態(tài)角。

保持架坐標(biāo)系中,第j個(gè)兜孔中心到保持架中心的位置向量為

(7)

式中,θp=2π(j-1)/z為第j個(gè)兜孔在保持架坐標(biāo)系中的方位角。

保持架兜孔坐標(biāo)系中,球心相對(duì)兜孔中心的位置向量為

(8)

式中,Tcp=T(θp,0,0)為保持架坐標(biāo)系到兜孔坐標(biāo)系的轉(zhuǎn)換矩陣。

如圖3所示,當(dāng)φc2<φg<φc1時(shí),球與保持架兜孔的碰撞點(diǎn)Og在兜孔球面內(nèi),當(dāng)φg≤φc2或φg≥φc1時(shí),碰撞點(diǎn)Og在兜孔球面與保持架內(nèi)圈或外圈圓柱面的相貫線(xiàn)上,兜孔球面與保持架內(nèi)圈和外圈的相貫線(xiàn)方程為

(9)

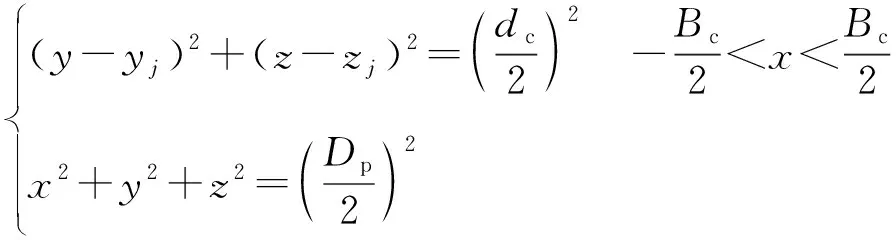
(10)

式中:yj,zj為保持架質(zhì)心在j個(gè)兜孔坐標(biāo)系中的坐標(biāo)值;Dc,dc,Bc分別為保持架的外徑、內(nèi)徑和寬度。

(11)

因此,邊界點(diǎn)Ocg的坐標(biāo)值滿(mǎn)足

(12)

(13)

(14)

(15)

當(dāng)φc2<φg<φc1時(shí),球與兜孔的碰撞點(diǎn)在兜孔坐標(biāo)系中的位置角為

(16)

(17)

(18)

式中,Tpg=T(φ1,0,φ3)為從兜孔坐標(biāo)系到接觸坐標(biāo)系的轉(zhuǎn)換矩陣。

球與兜孔的接觸變形量為

(19)

當(dāng)φg≤φc2或φg≥φc1時(shí),碰撞點(diǎn)Og相對(duì)球心Ob在兜孔坐標(biāo)系中的位置向量為

(20)

因此球與兜孔的碰撞點(diǎn)在兜孔坐標(biāo)系中的位置角為

(21)

(22)

(23)

此時(shí),球與兜孔的接觸變形量為

(24)

球與兜孔之間的法向力可計(jì)算得

(25)

式中,Kbc為球與保持架兜孔的載荷-變形系數(shù)。

則球與兜孔之間的切向力為

Ftc=μcQc

(26)

式中,μc為球與兜孔之間的摩擦因數(shù),設(shè)為恒定值。

保持架坐標(biāo)系中,接觸點(diǎn)相對(duì)保持架中心的位置向量為

(27)

式中,Tcg=TpgTcp為保持架坐標(biāo)系到接觸坐標(biāo)系的轉(zhuǎn)換矩陣。

球與兜孔接觸坐標(biāo)系中,球和保持架在接觸點(diǎn)處的線(xiàn)速度分別為

(28)

(29)

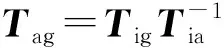
接觸點(diǎn)處保持架相對(duì)球的滑動(dòng)速度矢量為

(30)

則滑動(dòng)速度的大小為

(31)

對(duì)于保持架與球及引導(dǎo)套圈的相互作用,由于滑動(dòng)速度較大且接觸區(qū)較小,可以作為點(diǎn)或線(xiàn)接觸來(lái)計(jì)算瞬時(shí)磨損率,且一般認(rèn)為磨損主要發(fā)生在保持架上。保持架單個(gè)兜孔的瞬時(shí)磨損率可計(jì)算得

(32)

式中:Kc為保持架的磨損系數(shù);Hc為保持架材料的布氏硬度。

沿接觸橢圓長(zhǎng)軸和短軸的切向分力根據(jù)滑動(dòng)速度的方向確定

Ftcx=Ftcsinφcb

Ftcz=Ftccosφcb

(33)

接觸坐標(biāo)系中,球受到保持架的作用力矢量為

(34)

(35)

慣性坐標(biāo)系中,保持架受到單個(gè)球的作用力矢量為

(36)

為便于分析保持架受力對(duì)于保持架質(zhì)心運(yùn)動(dòng)的影響,定義了如圖4中所示的保持架方位坐標(biāo)系。方位坐標(biāo)系的原點(diǎn)Oca固定于保持架幾何中心,Xca軸沿軸承軸向,Zca軸徑向向外。將保持架受到的作用力在方位坐標(biāo)系中分解,得到各力在保持架質(zhì)心軸向、徑向和圓周運(yùn)動(dòng)方向上的分力。因此,在保持架方位坐標(biāo)系中,保持架受到單個(gè)球的作用力矢量為

圖4 保持架方位坐標(biāo)系OcaXcaYcaZcaFig.4 The cage azimuth coordinate system OcaXcaYcaZca

(37)

式中,Tica=T(α,0,0)為慣性坐標(biāo)系到保持架方位坐標(biāo)系的轉(zhuǎn)換矩陣。

球的方位坐標(biāo)系中,球受到保持架的力矩矢量為

(38)

保持架坐標(biāo)系中,保持架受到單個(gè)球的力矩矢量為

(39)

此外,對(duì)于方兜孔和圓兜孔保持架可采用類(lèi)似的方法建模,主要區(qū)別在于方兜孔和圓兜孔沿徑向是直的,球與保持架之間碰撞力在徑向分量為零,無(wú)需判斷碰撞點(diǎn)的徑向位置,且僅需繞Zp軸旋轉(zhuǎn)一次即可將保持架兜孔坐標(biāo)系轉(zhuǎn)換到接觸坐標(biāo)系,因此建模相對(duì)更容易,本文不再贅述。

1.4 保持架球與引導(dǎo)套圈的相互作用

圖5 保持架與引導(dǎo)擋邊的相互作用Fig.5 Interaction between cage and guide land

慣性坐標(biāo)系中,保持架中心相對(duì)外圈中心的位置向量為

(40)

(41)

保持架與外圈的接觸點(diǎn)在外圈坐標(biāo)系中的方位角為

(42)

(43)

式中,Trs=T(φs,0,0)為外圈坐標(biāo)系到接觸坐標(biāo)系的轉(zhuǎn)換矩陣。

保持架與引導(dǎo)套圈的接觸變形量為

(44)

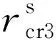
保持架與引導(dǎo)套圈之間的法向力由Hertz線(xiàn)接觸公式計(jì)算得

(45)

由此可得保持架與引導(dǎo)套圈之間的切向力

Ftr=μrQr

(46)

式中,μr為保持架與引導(dǎo)套圈之間的摩擦因數(shù),設(shè)為恒定值。

外圈坐標(biāo)系中,接觸點(diǎn)相對(duì)外圈中心的位置向量為

(47)

保持架坐標(biāo)系中,接觸點(diǎn)相對(duì)保持架中心的位置向量為

(48)

接觸坐標(biāo)系中,保持架和套圈引導(dǎo)面上接觸點(diǎn)處的線(xiàn)速度分別為

(49)

(50)

接觸坐標(biāo)系中,引導(dǎo)面上套圈相對(duì)保持架的滑動(dòng)速度為

(51)

則滑動(dòng)速度的大小為

(52)

保持架與引導(dǎo)套圈的接觸中,保持架引導(dǎo)面上的瞬時(shí)磨損率為

(53)

接觸坐標(biāo)系中,沿引導(dǎo)面軸向和周向的切向分力分別為

Ftrx=-Ftrsinφrc

Ftry=Ftrcosφrc

(54)

接觸坐標(biāo)系中,保持架受到引導(dǎo)套圈的作用力矢量為

(55)

(56)

式中,Tis=TrsTir為從慣性坐標(biāo)系到保持架與套圈接觸坐標(biāo)系的轉(zhuǎn)換矩陣。

保持架坐標(biāo)系中,保持架受到引導(dǎo)套圈的力矩矢量為

(57)

1.5 保持架所受的合力及合力矩

慣性坐標(biāo)系中保持架受到的合力為

(58)

保持架坐標(biāo)系中保持架受到的合力矩為

(59)

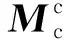
由此,即可得到保持架所受的合力以及合力矩,采用Runge-Kutta法對(duì)式(3)和式(4)進(jìn)行求解即可得到保持架任意時(shí)刻的位置和速度。

2 仿真結(jié)果分析

利用上述模型,以某高速角接觸球軸承為例,分析不同兜孔形狀以及兜孔間隙對(duì)保持架質(zhì)心運(yùn)動(dòng)、受力以及磨損率的影響。保持架所受的作用力均在保持架方位坐標(biāo)系中分析,保持架方位坐標(biāo)系的建立見(jiàn)圖4。軸承結(jié)構(gòu)和材料參數(shù)如表1所示。

表1 軸承幾何和材料參數(shù)Tab.1 Bearing geometry and material parameters

兜孔間隙Cb分別取0.096 mm,0.135 mm,0.240 mm和0.288 mm,對(duì)應(yīng)的間隙比(兜孔間隙Cb與引導(dǎo)間隙Cr的比值)分別為0.40,0.56,1.00和1.20。該軸承所處的工況為,軸向預(yù)載荷7 N,內(nèi)圈轉(zhuǎn)速30 000 r/min。需要說(shuō)明的是,由于本文計(jì)算程序采用Fortran語(yǔ)言編寫(xiě),大幅提高了計(jì)算效率,本文所有結(jié)果都選取仿真軸承運(yùn)轉(zhuǎn)達(dá)到穩(wěn)定后的值(取仿真1～2 s的結(jié)果,舍棄前1 s的結(jié)果)進(jìn)行分析。

2.1 保持架運(yùn)動(dòng)穩(wěn)定性分析

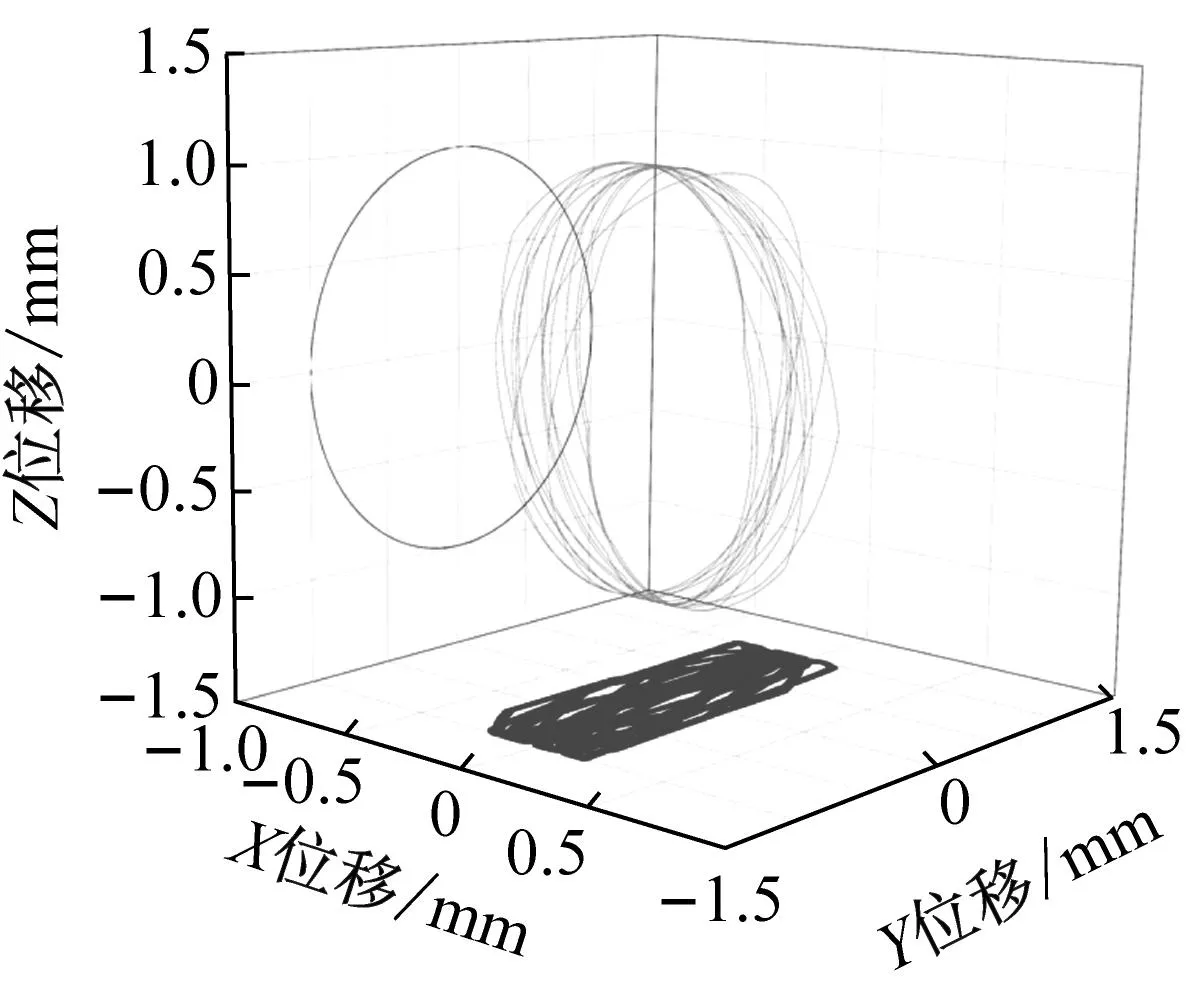
圖6分別給出了不同兜孔形狀的保持架在不同兜孔間隙下的三維質(zhì)心運(yùn)動(dòng)軌跡,需要說(shuō)明的是圖中空間曲線(xiàn)表示保持架的三維質(zhì)心運(yùn)動(dòng)軌跡,左側(cè)曲線(xiàn)和下側(cè)點(diǎn)分別是三維運(yùn)動(dòng)軌跡在YZ平面(徑向平面)以及XY面的投影,分別表示保持架在徑向平面的渦動(dòng)以及軸向擺動(dòng)。可以看出,隨著兜孔間隙的增大,方形和圓形兜孔保持架的三維質(zhì)心運(yùn)動(dòng)軌跡逐漸由圓柱形變?yōu)椴灰?guī)則形狀,而球形兜孔保持架的三維質(zhì)心運(yùn)動(dòng)軌跡則始終處于較規(guī)則的圓柱形。從XY平面的投影可以看出,隨著兜孔間隙的增大,方形和圓形兜孔保持架的渦動(dòng)軌跡逐漸由圓形變?yōu)槎噙呅?說(shuō)明保持架的運(yùn)動(dòng)越來(lái)越不穩(wěn)定,而球形兜孔保持架則始終處于穩(wěn)定的渦動(dòng)狀態(tài)。此外,在不同兜孔間隙下,方形和圓形保持架的渦動(dòng)軌跡直徑始終等于套圈引導(dǎo)間隙;而球形兜孔保持架則隨著兜孔間隙的增大而逐漸增大,且保持架質(zhì)心軌跡直徑等于或略小于兜孔間隙,當(dāng)兜孔間隙大于引導(dǎo)間隙時(shí),球形兜孔保持架的渦動(dòng)軌跡直徑才等于引導(dǎo)間隙。這說(shuō)明,不同間隙比下,方形和圓形保持架始終是由套圈引導(dǎo)的,而球形兜孔保持架則由球精確引導(dǎo)。從YZ面的投影可以看出,隨著保持架兜孔間隙的增大,三種兜孔形狀的保持架軸向擺動(dòng)均逐漸增加,且在不同兜孔間隙下,方形、圓形和球形兜孔保持架的軸向擺動(dòng)均依次逐漸減小,保持架的軸向擺動(dòng)與兜孔間隙以及兜孔形狀直接相關(guān)。

圖6 不同兜孔形狀以及兜孔間隙下的保持架三維質(zhì)心軌跡Fig.6 Three-dimensional centroid trajectory of cage under different pocket shapes and pocket gaps

為定量分析不同兜孔形狀以及兜孔間隙下各保持架的運(yùn)動(dòng)穩(wěn)定性,本文采用Ghaisas方法[21],即采用渦動(dòng)速度偏差比(保持架質(zhì)心運(yùn)動(dòng)速度的標(biāo)準(zhǔn)差與平均速度的比)作為保持架穩(wěn)定性判據(jù),渦動(dòng)速度偏差比越小,保持架越穩(wěn)定。不同兜孔形狀以及兜孔間隙下各保持架的渦動(dòng)速度偏差比如圖7所示。可以看出,在不同兜孔間隙下,球兜孔保持架的渦動(dòng)速度偏差比顯著低于方形和圓形兜孔保持架,說(shuō)明球兜孔保持架的穩(wěn)定性?xún)?yōu)于方形和圓形兜孔保持架;在間隙比小于1時(shí)(兜孔間隙為0.24時(shí),間隙比為1),方兜孔保持架穩(wěn)定性?xún)?yōu)于圓兜孔保持架,而在間隙比大于1時(shí),則是圓兜孔保持架更優(yōu)。

圖7 不同兜孔形狀及兜孔間隙下的保持架渦動(dòng)速度偏差比Fig.7 Cage whirl speed deviation ratio under different pocket shapes and pocket gaps

2.2 保持架受力分析

為進(jìn)一步深入探討保持架兜孔形狀對(duì)保持架質(zhì)心運(yùn)動(dòng)的影響,選取兜孔間隙為0.135 mm的保持架進(jìn)行分析,并將保持架的三維質(zhì)心運(yùn)動(dòng)及受力在保持架方位坐標(biāo)系中分解,分別對(duì)保持架徑向渦動(dòng)半徑、圓周渦動(dòng)速度和軸向擺動(dòng)以及相應(yīng)方向的受力進(jìn)行分析。

圖8和圖9分別給出了不同兜孔形狀的保持架徑向受力以及渦動(dòng)半徑,可以看出方形和圓形兜孔保持架在徑向主要受引導(dǎo)套圈的作用力,球?qū)Ρ３旨艿膹较蜃饔昧s為套圈的1/10,而球兜孔保持架由于被球限制了運(yùn)動(dòng)范圍,因此不與套圈發(fā)生碰撞。并且可以看出,圓形、方形和球形兜孔保持架在徑向的受力逐漸減小,因此,對(duì)應(yīng)的保持架渦動(dòng)半徑的波動(dòng)也逐漸減小,如圖9所示。對(duì)比圖8和圖9可以發(fā)現(xiàn),當(dāng)保持架與引導(dǎo)套圈發(fā)生較大碰撞時(shí),保持架的渦動(dòng)半徑將迅速減小,說(shuō)明引導(dǎo)套圈對(duì)保持架的徑向作用力不利于圓形渦動(dòng)軌跡的形成,而這也是球兜孔保持架質(zhì)心軌跡非常規(guī)則的原因。此外,圖9的結(jié)果表明方形和圓形兜孔保持架的渦動(dòng)直徑等于套圈引導(dǎo)間隙,而球形兜孔保持架的渦動(dòng)直徑等于兜孔間隙。但是在Gupta、葉振環(huán)、劉秀海、張濤等人的圓形兜孔保持架結(jié)果中,保持架的質(zhì)心渦動(dòng)半徑在逐漸增大或始終小于引導(dǎo)間隙,這是因?yàn)樗麄兎抡孑S承運(yùn)行的時(shí)間較短(小于0.1 s),而動(dòng)力學(xué)程序中保持架的質(zhì)心位置初值是在軸承中心,仿真0.1 s還不足以使保持架運(yùn)轉(zhuǎn)到穩(wěn)定的狀態(tài),因此他們的分析雖有參考價(jià)值,但由于保持架未運(yùn)轉(zhuǎn)到穩(wěn)定狀態(tài),結(jié)果是不夠準(zhǔn)確的。

(a) 方形兜孔

(b) 圓形兜孔

(a) 方形兜孔

(b) 圓形兜孔

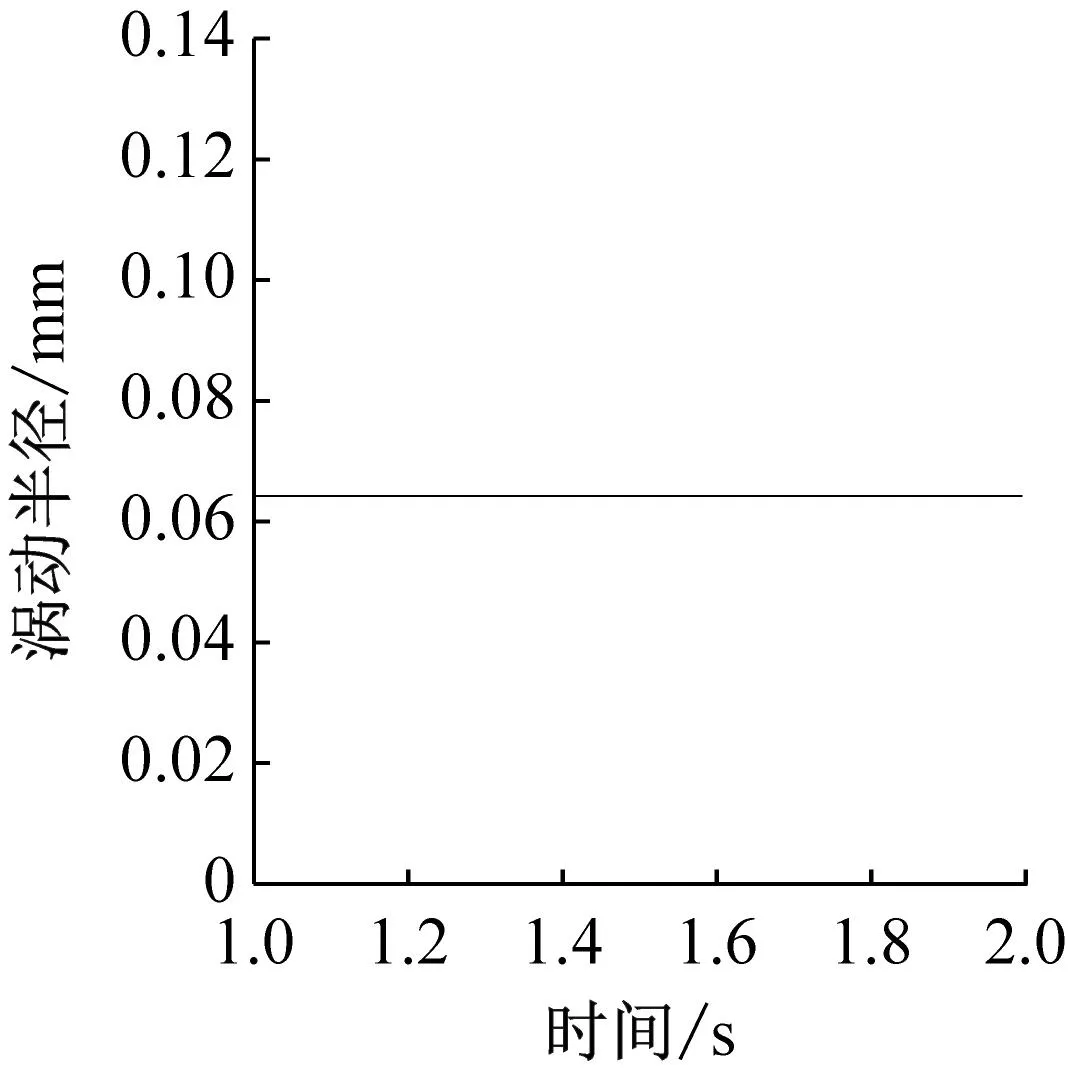
(c) 球形兜孔圖9 不同兜孔形狀保持架的渦動(dòng)半徑Fig.9 Cage whirl radius of different pockets

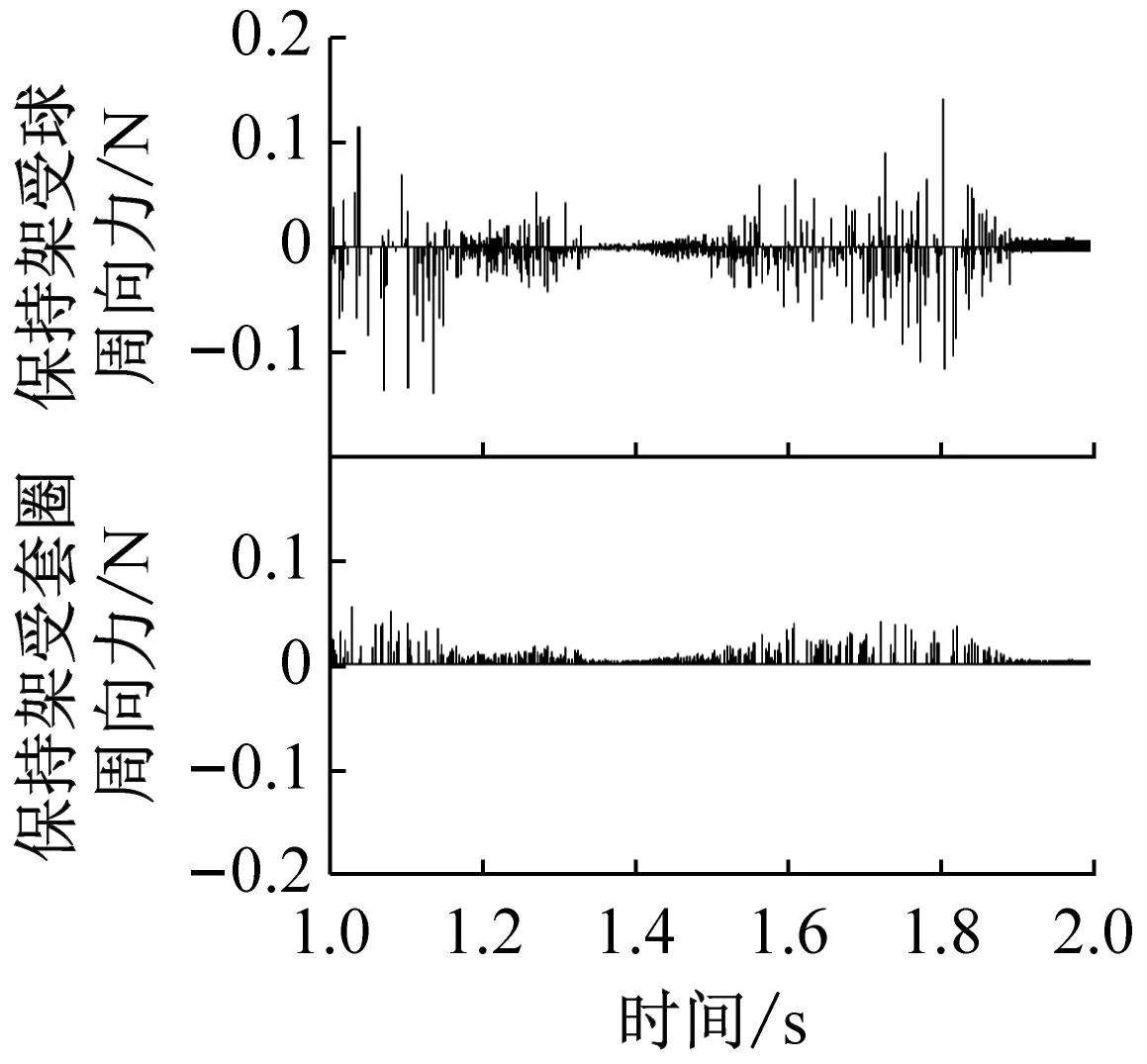
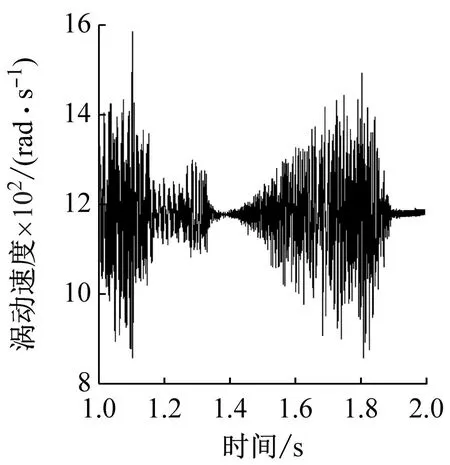
圖10和圖11分別給出了不同兜孔形狀的保持架周向受力以及渦動(dòng)速度,需要指出的是由于保持架方位坐標(biāo)系的Yca軸與保持架渦動(dòng)方向相反,因此數(shù)值為正的周向力是阻礙保持架的渦動(dòng)的,而數(shù)值為負(fù)的周向力驅(qū)動(dòng)著保持架的渦動(dòng)。從圖10可以看出,對(duì)于方兜孔和圓兜孔,保持架在周向主要承受鋼球的作用力,而引導(dǎo)套圈對(duì)保持架作用力較小且始終是阻力,這是因?yàn)楸３旨苁怯晒潭ǖ耐馊σ龑?dǎo)的,且外圈對(duì)保持架周向作用力是由摩擦力產(chǎn)生的;而球?qū)Ρ３旨艿闹芟蜃饔昧χ饕膳鲎擦Τ袚?dān),當(dāng)球超前于保持架的運(yùn)動(dòng)時(shí),球驅(qū)動(dòng)著保持架的渦動(dòng),當(dāng)球滯后于保持架的運(yùn)動(dòng)時(shí),球阻礙著保持架的渦動(dòng)。圖10中球?qū)Ρ３旨艿淖饔昧τ姓胸?fù),因此時(shí)而驅(qū)動(dòng)時(shí)而阻礙并維持著保持架的渦動(dòng)速度處于動(dòng)態(tài)平衡態(tài)。由于球與圓兜孔保持架的沖擊力較大,這也就導(dǎo)致了圖11中保持架的渦動(dòng)速度波動(dòng)較大,而對(duì)于球兜孔保持架則由于碰撞沖擊力很小,因此球兜孔保持架的渦動(dòng)速度也就非常平穩(wěn)。

(a) 方形兜孔

(b) 圓形兜孔

(c) 球形兜孔圖10 不同兜孔形狀保持架的周向受力Fig.10 Circumferential force on the cage of different pockets

(b) 圓形兜孔

(c) 球形兜孔圖11 不同兜孔形狀保持架的渦動(dòng)速度Fig.11 Cage whirl speed of different pockets

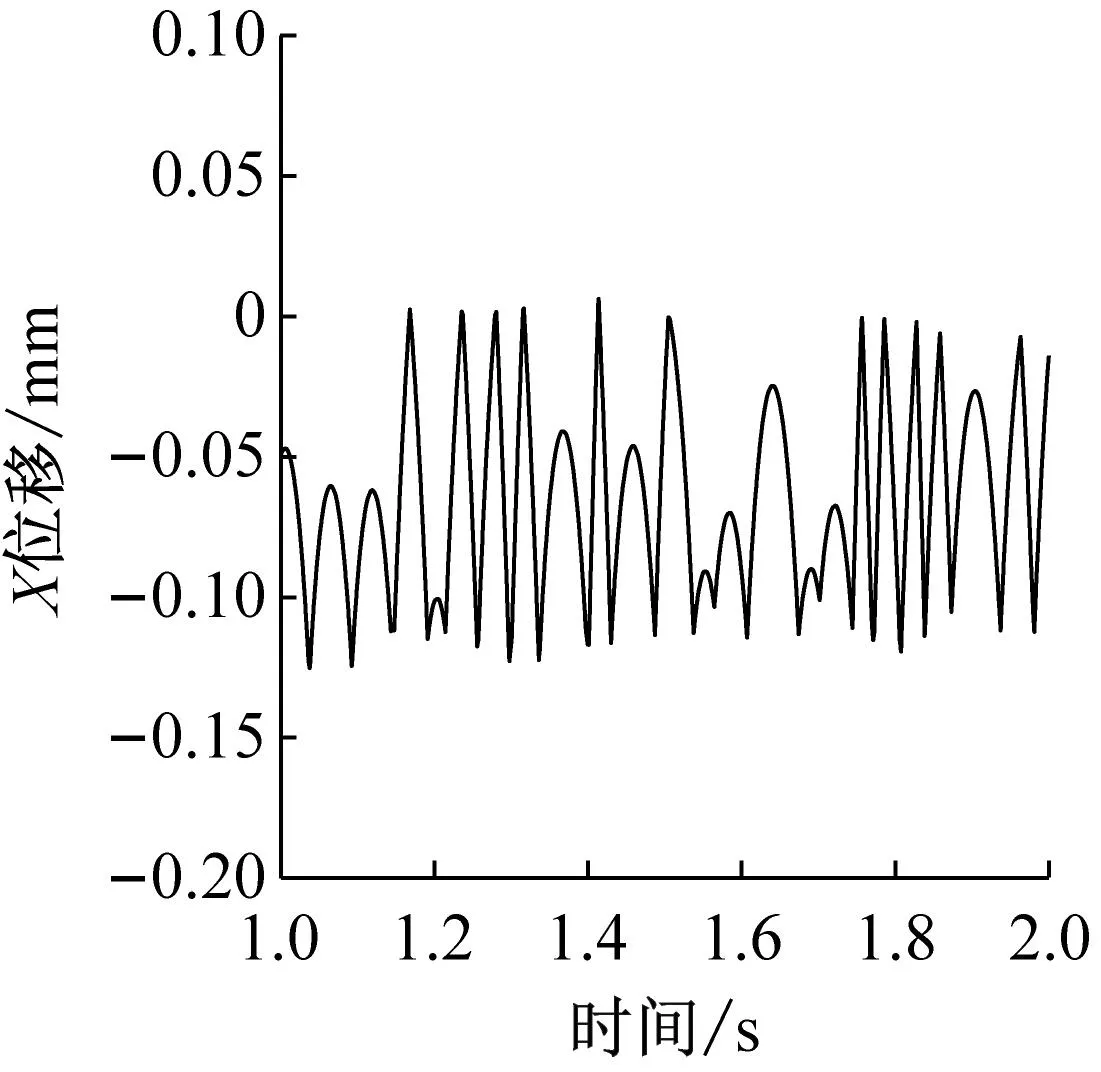
圖12和圖13分別給出了不同兜孔形狀的保持架軸向受力以及軸向擺動(dòng)位移,可以看出,在軸向上,保持架僅受球的作用力(對(duì)于方兜孔和圓兜孔保持架還受引導(dǎo)套圈的摩擦力在軸向的分量,但由于保持架渦動(dòng)速度相對(duì)于軸向擺動(dòng)速度大得多,因此摩擦力在軸向的分量約為10-6N級(jí),可忽略不計(jì)),因此保持架在軸向上的擺動(dòng)僅與球?qū)ζ渥饔昧ο嚓P(guān)。與徑向力和周向力類(lèi)似,球兜孔保持架在軸向受力也非常小,對(duì)應(yīng)的保持架軸向擺動(dòng)量也是很小的。而對(duì)于方兜孔和圓兜孔,方兜孔保持架在軸向受力大小和頻率均小于圓兜孔保持架,對(duì)應(yīng)的方兜孔保持架軸向擺動(dòng)頻率小于圓兜孔保持架,但是擺動(dòng)范圍卻較圓兜孔更大,這是因?yàn)閳A兜孔保持架所受軸向力雖然更大,但是頻率也更高,當(dāng)保持架還來(lái)不及沿軸向正向(負(fù)向)產(chǎn)生較大的位移時(shí),負(fù)(正)的軸向作用力就使得保持架沿負(fù)(正)向運(yùn)動(dòng)了,使得圓兜孔保持架在軸向處于一個(gè)較穩(wěn)定的動(dòng)態(tài)平衡狀態(tài)。

(a) 方形兜孔

(b) 圓形兜孔

(c) 球形兜孔圖12 不同兜孔形狀保持架的軸向受力Fig.12 Axial force on the cage of different pockets

(a) 方形兜孔

(b) 圓形兜孔

(c) 球形兜孔圖13 不同兜孔形狀保持架的軸向擺動(dòng)Fig.13 Cage axial motion of different pockets

2.3 保持架磨損分析

圖14為不同兜孔形狀保持架兜孔面、引導(dǎo)面以及總的時(shí)間平均磨損率,保持架總的時(shí)間平均磨損率是兜孔面和引導(dǎo)面磨損率之和。時(shí)間平均磨損率表示的是一段時(shí)間內(nèi)磨損量的平均值。可以看出,隨著保持架兜孔間隙的增大,三種兜孔形狀的保持架兜孔時(shí)間平均磨損率逐漸降低,且圓兜孔保持架的兜孔時(shí)間平均磨損率遠(yuǎn)大于方兜孔和圓兜孔保持架。而對(duì)于保持架引導(dǎo)面的時(shí)間平均磨損率,當(dāng)兜孔間隙小于引導(dǎo)間隙時(shí),球兜孔保持架不與套圈相接觸,因此引導(dǎo)面的時(shí)間平均磨損率為零;當(dāng)兜孔間隙大于引導(dǎo)間隙時(shí),球兜孔保持架引導(dǎo)面開(kāi)始出現(xiàn)磨損;圓兜孔和方兜孔保持架引導(dǎo)面的時(shí)間平均磨損率隨著兜孔間隙的增加逐漸減小,且圓兜孔保持架引導(dǎo)面的時(shí)間平均磨損率始終大于方兜孔;此外,對(duì)比保持架兜孔面與引導(dǎo)面的磨損可以看出,球兜孔保持架兜孔面的磨損始終遠(yuǎn)大于引導(dǎo)面,而方兜孔和圓兜孔保持架引導(dǎo)面的磨損始終大于兜孔面的磨損,再一次說(shuō)明了球兜孔保持架是由球引導(dǎo)的,而方兜孔和圓兜孔保持架則是由引導(dǎo)套圈引導(dǎo)的。從圖14(c)可以看出三種兜孔形狀的保持架總的磨損均隨著兜孔間隙的增加而減小,這與圖7所反映的保持架穩(wěn)定性是相反的,說(shuō)明保持架越穩(wěn)定,保持架的磨損率反而更低。這是因?yàn)楫?dāng)保持架處于穩(wěn)定的渦動(dòng)狀態(tài)時(shí),保持架與球以及引導(dǎo)套圈之間的作用力雖然比較小,但是作用頻率卻高得多,因此接觸磨損的時(shí)間更長(zhǎng),保持架的磨損反而更大。所以,保持架的設(shè)計(jì)需要綜合考慮保持架的穩(wěn)定性和磨損,不能僅單獨(dú)地追求更好的保持架穩(wěn)定性或更低的磨損率。

(a) 方形兜孔

(b) 圓形兜孔

(c) 球形兜孔圖14 不同兜孔形狀保持架的時(shí)間平均磨損率Fig.14 Cage time-average wear rate of different pockets

3 試驗(yàn)驗(yàn)證

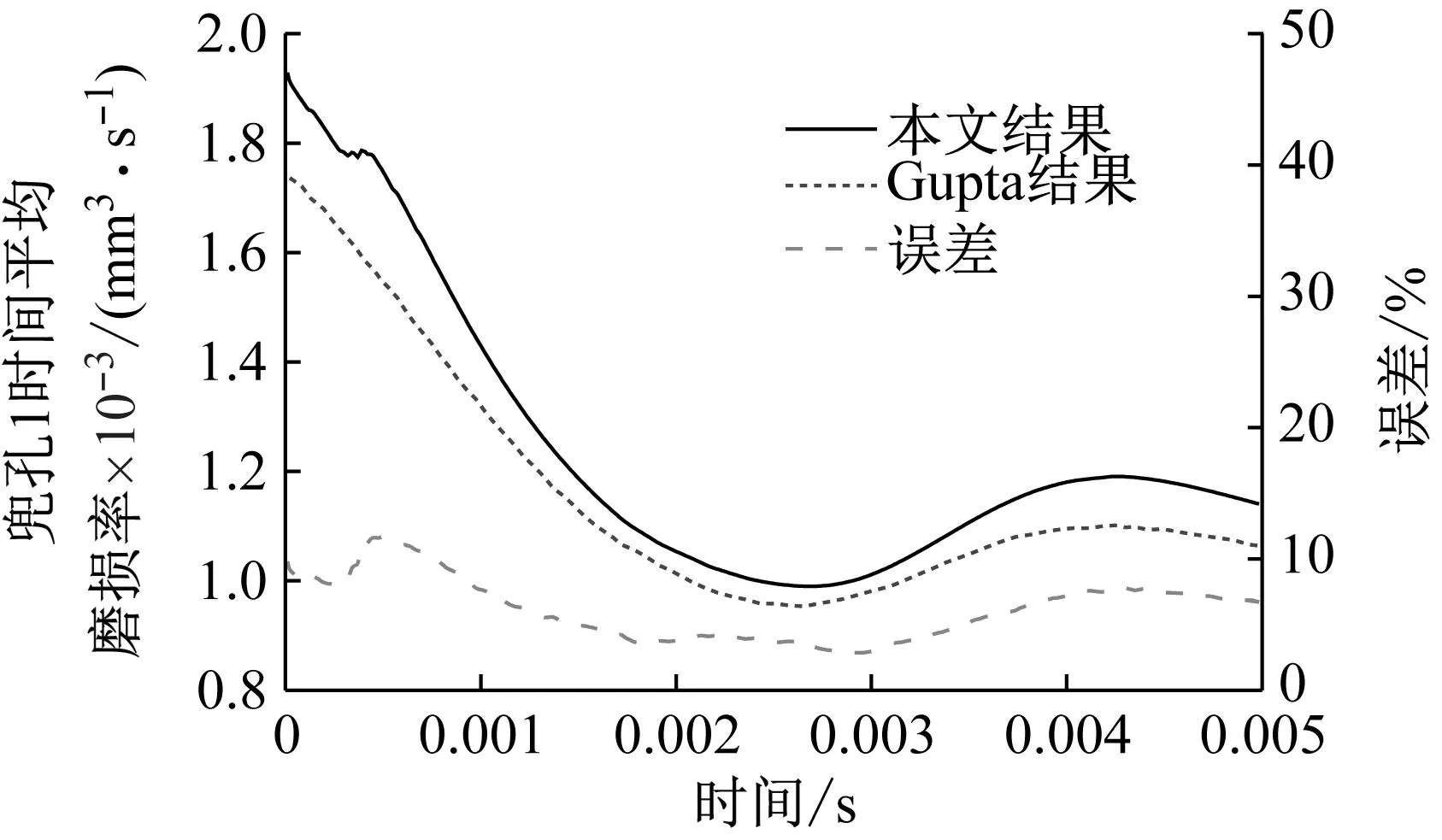
為了驗(yàn)證本文提出的三種兜孔形狀的保持架動(dòng)力學(xué)數(shù)值仿真模型的正確性,與Gupta的2號(hào)角接觸球軸承的算例對(duì)比驗(yàn)證圓形兜孔保持架動(dòng)力學(xué)模型得程序。軸承的工況為內(nèi)圈轉(zhuǎn)速30 000 r/min,推力載荷為5 000 N,旋轉(zhuǎn)徑向載荷為4 000 N。本文程序1號(hào)兜孔的磨損率及保持架質(zhì)心軌跡與Gupta的結(jié)果如圖15所示。本文程序磨損率與Gupta結(jié)果趨勢(shì)一致,大小基本相等,最大誤差不超過(guò)12%,且保持架質(zhì)心軌跡與Gupta也基本一致,因此本文圓柱形兜孔保持架動(dòng)力學(xué)程序正確性和可靠性得到了驗(yàn)證。方形兜孔和球形兜孔保持架動(dòng)力學(xué)結(jié)果報(bào)道較少,下面將用課題組設(shè)計(jì)的高速角接觸球軸承保持架動(dòng)態(tài)特性試驗(yàn)機(jī)進(jìn)行試驗(yàn)驗(yàn)證。

(a) 磨損率

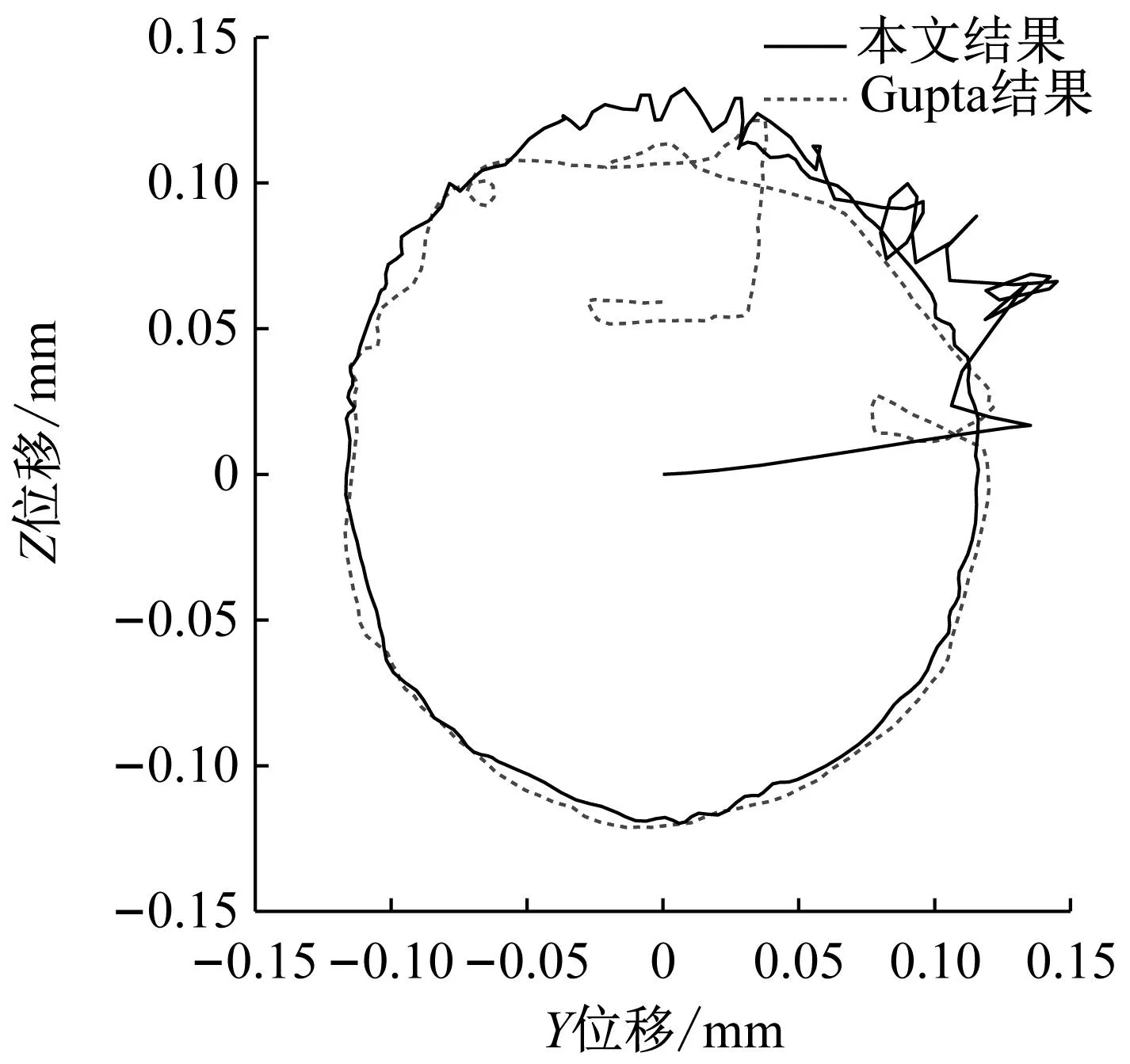
(b) 質(zhì)心軌跡圖15 本文圓柱兜孔保持架動(dòng)力學(xué)結(jié)果與Gupta結(jié)果對(duì)比Fig.15 Comparison between the cylindrical pocket cage dynamic results of current model and Gupta’s model

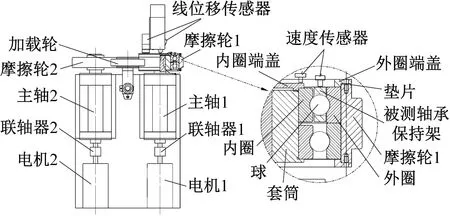
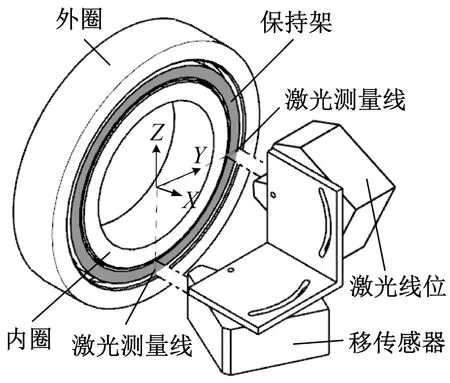
為進(jìn)一步驗(yàn)證本文提出的三種兜孔形狀的保持架動(dòng)力學(xué)數(shù)值仿真模型的正確性,采用課題組設(shè)計(jì)的高速角接觸球軸承保持架動(dòng)態(tài)特性試驗(yàn)機(jī)[22-23]分別對(duì)這三種兜孔形狀的保持架進(jìn)行試驗(yàn)探究,試驗(yàn)機(jī)的結(jié)構(gòu)圖如圖16所示。電機(jī)1通過(guò)聯(lián)軸器直接帶動(dòng)被試軸承內(nèi)圈旋轉(zhuǎn),電機(jī)2通過(guò)帶動(dòng)摩擦輪2、加載輪以及摩擦輪1,從而帶動(dòng)被試軸承外圈旋轉(zhuǎn),從而實(shí)現(xiàn)被試軸承內(nèi)外圈在一定轉(zhuǎn)速范圍內(nèi)任意同向或反向旋轉(zhuǎn)。選用兩個(gè)如圖16所示的LJ-G015K激光線(xiàn)位移傳感器測(cè)量保持架的三維質(zhì)心軌跡,其X軸測(cè)量范圍為(高度)15±2.3 mm,Z軸測(cè)量范圍距離7 mm;激光線(xiàn)位移傳感器打出來(lái)的激光線(xiàn)是由一排激光點(diǎn)組成的,其中有效測(cè)量點(diǎn)為800個(gè),兩相鄰激光點(diǎn)的間距恒定為10 μm,即800個(gè)點(diǎn)中700個(gè)點(diǎn)為有效數(shù)據(jù),兩端各50點(diǎn)為無(wú)效數(shù)據(jù),在有效測(cè)量范圍內(nèi)被測(cè)物體超量程時(shí)顯示為999.999的無(wú)效數(shù)據(jù),根據(jù)無(wú)效點(diǎn)的個(gè)數(shù)變化情況及各個(gè)點(diǎn)之間的距離即可算出被測(cè)物體X向的位移,被測(cè)物體Z或Y向的位移可直接由得到的有效數(shù)據(jù)取平均值計(jì)算,由此就可以在不改變軸承結(jié)構(gòu)的情況下同步測(cè)得保持架的徑向和軸向位移,也就是得到保持架的空間三維質(zhì)心軌跡。被試軸承參數(shù)如表2所示。軸承內(nèi)圈轉(zhuǎn)速為1 000 r/min,外圈固定,軸向預(yù)載荷為100 N。需要說(shuō)明的是,由于激光線(xiàn)位移傳感器尺寸的限制,試驗(yàn)所用的軸承較大,本試驗(yàn)主要用于驗(yàn)證所建立數(shù)值仿真模型的正確性。

(a)

(b)

(c)

(d)圖16 試驗(yàn)機(jī)結(jié)構(gòu)圖以及測(cè)量原理圖Fig.16 Test machine structure diagram and measurement principle diagram

表2 被試軸承幾何參數(shù)Tab.2 Geometric parameters of the tested bearing

圖17～19為數(shù)值仿真和試驗(yàn)得到的三種兜孔形狀保持架的三位質(zhì)心軌跡以及Y向位移響應(yīng),從圖中可以看出,三種兜孔形狀的保持架質(zhì)心軌跡形狀和軌跡半徑都與仿真結(jié)果接近,且從Y向位移響應(yīng)的結(jié)果看,仿真結(jié)果和試驗(yàn)結(jié)果也保持較好的同步性,說(shuō)明仿真和試驗(yàn)得到的保持架渦動(dòng)速度是一致的,從而在保持架質(zhì)心位移和速度兩個(gè)方面驗(yàn)證了仿真結(jié)果的可靠性與準(zhǔn)確性。

(a) 數(shù)值仿真三維質(zhì)心軌跡

(b) 試驗(yàn)三維質(zhì)心軌跡

(b) 試驗(yàn)三維質(zhì)心軌跡

(c) Y方向位移響應(yīng)圖18 圓兜孔保持架質(zhì)心運(yùn)動(dòng)Fig.18 Cylindrical pocket cage motion

(a) 數(shù)值仿真三維質(zhì)心軌跡

(b) 試驗(yàn)三維質(zhì)心軌跡

(c) Y方向位移響應(yīng)圖19 球兜孔保持架質(zhì)心運(yùn)動(dòng)Fig.19 Spherical pocket cage motion

此外,試驗(yàn)結(jié)果還表明方形和圓形兜孔保持架的質(zhì)心軌跡直徑等于保持架引導(dǎo)間隙,而球兜孔保持架的質(zhì)心軌跡直徑等于兜孔間隙,從而試驗(yàn)證明了圓形和方形兜孔保持架由套圈引導(dǎo),而球兜孔保持架由球引導(dǎo);并且試驗(yàn)結(jié)果還表明方形、圓形和球形兜孔保持架的軸向擺動(dòng)范圍逐漸減小,這些與仿真分析結(jié)論均是一致的。

4 結(jié) 論

本文建立了方形、圓形和球形兜孔保持架的高速角接觸球軸承動(dòng)力學(xué)數(shù)值仿真模型,并通過(guò)試驗(yàn)驗(yàn)證了三種兜孔形狀保持架動(dòng)力學(xué)模型的正確性,在此基礎(chǔ)上,詳細(xì)探討了保持架兜孔形狀及兜孔間隙對(duì)保持架動(dòng)力學(xué)特性的影響,并得出如下結(jié)論:

(1) 試驗(yàn)和仿真結(jié)果均表明方形和圓形兜孔保持架由套圈引導(dǎo),而球兜孔保持架由球引導(dǎo);方形、圓形和球形保持架的軸向擺動(dòng)范圍依次減小。

(2) 隨著兜孔間隙的增大,三種兜孔形狀的保持架穩(wěn)定性均逐漸降低,保持架軸向擺動(dòng)范圍逐漸增大,且球兜孔保持架穩(wěn)定性遠(yuǎn)高于方兜孔和圓兜孔保持架穩(wěn)定性,軸向擺動(dòng)范圍也低于方兜孔和圓兜孔保持架;間隙比小于1時(shí),方兜孔保持架穩(wěn)定性?xún)?yōu)于圓兜孔,而間隙比大于1時(shí)則劣于圓兜孔。

(3) 保持架的運(yùn)動(dòng)與鋼球和套圈之間的受力相關(guān)。保持架的徑向渦動(dòng)半徑主要受保持架和套圈之間的作用力影響,保持架的軸向擺動(dòng)以及周向速度主要受保持架兜孔與球之間的作用力影響。球兜孔保持架與球和套圈之間的作用非常小,因此運(yùn)動(dòng)很穩(wěn)定。

(4) 方形和圓形兜孔保持架的磨損主要發(fā)生在引導(dǎo)面上,而球兜孔保持架的磨損主要發(fā)生在兜孔面上。隨著兜孔間隙的增大,三種兜孔保持架的磨損率均逐漸降低,且球兜孔保持架的磨損率遠(yuǎn)高于另兩種保持架。