不同連接構(gòu)造的預(yù)制拼裝鋼管混凝土橋墩數(shù)值模擬與地震響應(yīng)特點(diǎn)

陳挺地, 王勝斌, 馮克巖, 李建中

(1. 同濟(jì)大學(xué) 土木工程防災(zāi)國(guó)家重點(diǎn)實(shí)驗(yàn)室, 上海 200092;2. 安徽省交通規(guī)劃設(shè)計(jì)研究總院股份有限公司, 合肥 231262; 3. 天津市政工程設(shè)計(jì)研究總院有限公司, 天津 300392)

預(yù)制拼裝技術(shù)因具有施工工期短、環(huán)境污染小等特點(diǎn),在建筑和橋梁領(lǐng)域得到了廣泛的應(yīng)用[1-3]。而隨著國(guó)內(nèi)外對(duì)“快速橋梁建設(shè)”要求[4]的提出,結(jié)合預(yù)制拼裝技術(shù)的橋梁下部結(jié)構(gòu)施工方法和工藝也廣泛受到學(xué)者和設(shè)計(jì)者的關(guān)注[5-6]。

與傳統(tǒng)鋼筋混凝土橋墩相比,鋼管混凝土(concrete filled steel tube,CFT)橋墩具有承載力高、滯回耗能強(qiáng)和震后低損傷等優(yōu)點(diǎn)[7-8],且易與預(yù)制拼裝橋墩技術(shù)結(jié)合,方便施工。文獻(xiàn)指出,預(yù)制拼裝橋墩結(jié)構(gòu)的抗震性能主要取決于預(yù)制橋墩與基底的節(jié)點(diǎn)連接特性[9-10]。為了使預(yù)制橋墩與傳統(tǒng)的現(xiàn)澆橋墩具有相同的承載力、變形能力和耗能能力,需要對(duì)連接部位采取一定措施以防止受拉構(gòu)件錨固失效[11]。

Goto等[12]較早地對(duì)“承插連接”(socket connection,SC)鋼管混凝土橋墩在水平加載作用下的力學(xué)性能進(jìn)行研究。隨后,Stephens等[13-14]提出了若干節(jié)點(diǎn)構(gòu)造細(xì)節(jié)以改善承插連接節(jié)點(diǎn)的傳力機(jī)理,并試驗(yàn)發(fā)現(xiàn):在水平地震力的作用下,承插連接墩底部會(huì)出現(xiàn)鋼管局部屈曲,并發(fā)生鋼管撕裂破壞。可見,承插連接橋墩損傷主要集中在墩底,在分析中需考慮這種損傷。為此,Goto等[15-16]建立了考慮墩底損傷的三維實(shí)體有限元橋墩模型。Shen等[17]則采用纖維梁-柱單元建立模型,在插入承臺(tái)鋼管與承臺(tái)混凝土的接觸面,采用設(shè)置接觸彈簧來(lái)模擬擠壓和摩擦等行為。為了提高計(jì)算效率,Stephens等[18]在墩底設(shè)置零長(zhǎng)度纖維單元模擬鋼管屈曲、屈曲后撕裂以及鋼管與承臺(tái)混凝土的黏結(jié)滑移。

此外,為了增強(qiáng)結(jié)構(gòu)的耗能能力以及自復(fù)位能力,學(xué)者提出了同時(shí)采用預(yù)應(yīng)力筋以及耗能鋼筋的“混合連接”(hybrid connection,HC)構(gòu)造[19]。此類橋墩一方面具有“混合搖擺”的力學(xué)特性,能在地震中表現(xiàn)出小損傷的特性[20];另一方面,借用加固墩身的理念(如超高性能混凝土[21]、纖維增強(qiáng)聚合物包裹[22]或鋼管混凝土加固[23-24]),解決了傳統(tǒng)鋼筋混凝土“搖擺墩”墩底易損傷的缺點(diǎn)。其有限元模型需要考慮接縫處的搖擺現(xiàn)象,如今常采用多彈簧接觸模型模擬接縫的搖擺行為[25],能取得令人滿意的計(jì)算效率和精度。

目前,針對(duì)兩種橋墩的抗震研究主要集中在擬靜力作用下的性能評(píng)估,但對(duì)于動(dòng)力作用下的響應(yīng)特點(diǎn)鮮有研究,且SC連接方式的橋墩,內(nèi)部設(shè)置預(yù)應(yīng)力對(duì)其地震響應(yīng)的影響也未有詳細(xì)分析。為此,本文以承插連接和混合連接的兩種無(wú)黏結(jié)預(yù)應(yīng)力鋼管混凝土橋墩為研究對(duì)象,介紹了各自連接細(xì)部構(gòu)造,并結(jié)合運(yùn)動(dòng)特征分別建立數(shù)值分析模型,其中,承插連接橋墩模型能模擬出鋼管屈曲、屈曲后撕裂和鋼管入承臺(tái)部分與周圍混凝土黏結(jié)滑移,而混合連接鋼管混凝土橋墩模型能考慮接縫搖擺等非線性行為。基于已完成的擬靜力試驗(yàn),驗(yàn)證兩個(gè)橋墩模型的有效性。最后,結(jié)合一座4跨連續(xù)梁橋,選取10條實(shí)際地震記錄作為輸入,對(duì)比了地震作用下兩種橋墩的動(dòng)力響應(yīng)特點(diǎn),為實(shí)際橋梁工程設(shè)計(jì)提供參考依據(jù)。

1 預(yù)制拼裝鋼管混凝土橋墩構(gòu)造

承插連接鋼管混凝土橋墩典型構(gòu)造如圖1所示。承臺(tái)中預(yù)留插槽,預(yù)制鋼管混凝土墩身插入承臺(tái)內(nèi)部,鋼管在墩底截面不斷開。需注意,以往的承插連接的鋼管混凝土橋墩并不設(shè)置預(yù)應(yīng)力筋(以下簡(jiǎn)稱為無(wú)預(yù)應(yīng)力承插式鋼管混凝土橋墩),僅依靠上部結(jié)構(gòu)恒載提供較小自復(fù)位趨勢(shì),而本文在此連接結(jié)構(gòu)的基礎(chǔ)上引入無(wú)黏結(jié)預(yù)應(yīng)力筋增強(qiáng)其自復(fù)位效果,即在橋墩中心預(yù)留預(yù)應(yīng)力筋孔道,內(nèi)部設(shè)置后張無(wú)黏結(jié)預(yù)應(yīng)力筋,提高結(jié)構(gòu)自復(fù)位能力。此橋墩的鋼管不僅對(duì)內(nèi)部核心混凝土提供約束,提高混凝土的抗壓性能,還同時(shí)在地震作用時(shí)與混凝土共同作用,抵抗水平力產(chǎn)生的彎矩,并在自身鋼材屈服后提供耗能能力。但隨著側(cè)向位移的增大,橋墩受壓側(cè)鋼管易發(fā)生屈曲并鼓出,此時(shí)該區(qū)域鋼管對(duì)同樣處在受壓側(cè)的混凝土幾乎沒有約束作用,導(dǎo)致結(jié)構(gòu)水平承載力下降。

圖1 承插連接鋼管混凝土橋墩Fig.1 Concrete filled steel tube column with socket connection

混合連接的鋼管混凝土橋墩典型構(gòu)造如圖2所示。橋墩主體為預(yù)制鋼管混凝土柱,底部設(shè)有伸出墩底截面的耗能鋼筋,并通過波紋管灌漿與承臺(tái)連接。可見,鋼管在墩底處斷開,不與混凝土共同抵抗彎矩,僅對(duì)核心混凝土產(chǎn)生約束作用。此外,橋墩截面中心處同樣設(shè)置后張預(yù)應(yīng)力筋,因此,地震作用下,混合連接的鋼管混凝土橋墩具有“混合搖擺”的力學(xué)特性:耗能鋼筋提供滯回耗能能力,減小結(jié)構(gòu)響應(yīng);結(jié)構(gòu)自重和預(yù)應(yīng)力筋提供“恢復(fù)力”,有效減小結(jié)構(gòu)的殘余位移。

圖2 混合連接鋼管混凝土橋墩Fig.2 Concrete filled steel tube column with hybrid connection

2 橋墩數(shù)值模型

為研究無(wú)黏結(jié)預(yù)應(yīng)力鋼管混凝土橋墩在承插連接與混合連接下地震響應(yīng),需采用OpenSees開源平臺(tái)建立了兩種連接構(gòu)造下的鋼管混凝土橋墩有限元模型。

2.1 承插連接橋墩模型

承插連接鋼管混凝土橋墩數(shù)值模型需能再現(xiàn)出加載過程中,鋼管入承臺(tái)部分與周邊混凝土的黏結(jié)滑移、鋼管局部屈曲效應(yīng)以及屈曲后撕裂等過程。為此,本章采用OpenSees的纖維單元,建立能考慮上述接觸和損傷過程的鋼管混凝土橋墩空間有限元模型,如圖3(a)所示。墩身主體采用纖維梁?jiǎn)卧M,纖維劃分如圖3(b)“纖維劃分Ⅰ”所示。其中鋼管纖維采用彈塑性滯回本構(gòu),以模擬鋼材的滯回耗能,如圖3(d)所示。假定無(wú)黏結(jié)預(yù)應(yīng)力筋始終處于彈性狀態(tài),采用桿單元模擬。

圖3 SC橋墩有限元模型示意圖Fig.3 Details of SC column finite element model

由于承插連接的構(gòu)造特點(diǎn),橋墩截面鋼管與混凝土?xí)餐瑓⑴c縱向受力,此外,鋼管還要側(cè)向約束內(nèi)部核心混凝土,因此,處于兩向受拉狀態(tài),韓林海[26]針對(duì)這種現(xiàn)象進(jìn)行研究,提出了韓林海本構(gòu)以描述這種約束狀態(tài)下的混凝土應(yīng)力-應(yīng)變關(guān)系。本文采用韓林海本構(gòu)模擬墩身截面混凝土纖維,如圖3(c)所示。

如前所述,采用承插式連接的鋼管混凝土橋墩,在地震作用下,鋼管與核心混凝土共同抵抗地震產(chǎn)生的彎矩,橋墩底部鋼管一側(cè)受拉,一側(cè)受壓,受壓側(cè)鋼管會(huì)發(fā)生局部屈曲,如圖4(a)所示。在鋼管發(fā)生局部屈曲后,在屈曲范圍內(nèi)不能對(duì)核心混凝土形成有效約束。為了考慮鋼管局部屈曲效應(yīng),本文采用零長(zhǎng)度纖維單元模擬鋼管屈曲效應(yīng),具體模擬方法如下:

(a) 鋼管屈曲鼓出

(b) 鋼管環(huán)向裂縫圖4 承插連接橋墩試件試驗(yàn)現(xiàn)象Fig.4 Experimental phenomenon on SC specimen

(1) 有限元模型中在墩底設(shè)置一零長(zhǎng)度纖維單元,其截面纖維劃分如圖3(b)中“纖維劃分Ⅱ”

(2) 鋼管纖維的應(yīng)力-應(yīng)變關(guān)系采用理想彈塑性本構(gòu),初始剛度等于鋼材彈性模量Es,屈后剛度取為0.01Es。

(3) 假設(shè)局部屈曲對(duì)鋼管的影響可由應(yīng)力下降模擬,采用Shen等提出的考慮鋼管局部屈曲的鋼管纖維應(yīng)力-應(yīng)變關(guān)系,如圖5所示,即在第三象限,當(dāng)鋼管纖維壓應(yīng)變達(dá)到屈曲應(yīng)變?chǔ)舃1時(shí),應(yīng)力進(jìn)入下降段,εb1由Denavit提出的公式計(jì)算[27]

圖5 考慮屈曲、撕裂的鋼管本構(gòu)Fig.5 Steel tube constitutive relationship

(1)

式中:εb1為屈服應(yīng)變;D為橋墩直徑;t為鋼管厚度;Fy為鋼材屈服強(qiáng)度。應(yīng)力下降至σb2后保持恒定,此時(shí)屈曲應(yīng)力σb2和對(duì)應(yīng)的屈曲應(yīng)變?chǔ)舃2由下式計(jì)算

σb2=ασb1

(2)

(3)

式中,α為鋼管屈曲應(yīng)力下降系數(shù),本文取α=0.6。

(4) 假設(shè)鋼管局部屈曲的高度為L(zhǎng)b,Stephens等[18]建議Lb取為8倍鋼管厚度。在鋼管局部屈曲范圍內(nèi),不考慮鋼管對(duì)混凝土的約束,混凝土應(yīng)力-應(yīng)變關(guān)系取無(wú)約束素混凝土本構(gòu)。

(5) 地震作用下橋墩插入承臺(tái)凹槽部分的鋼管與承臺(tái)凹槽壁會(huì)發(fā)生黏結(jié)滑移,降低結(jié)構(gòu)剛度。本文采用鋼管纖維等效自由變形長(zhǎng)度Le模擬這種黏結(jié)滑移效應(yīng),即假設(shè)承臺(tái)以下鋼管纖維應(yīng)變均勻分布于等效自由變形長(zhǎng)度Le中。Stephens等建議Le取為0.78倍承插深度。

(6) 轉(zhuǎn)化鋼管纖維和無(wú)約束素混凝土纖維的應(yīng)力-應(yīng)變關(guān)系為力-位移關(guān)系。對(duì)于鋼管纖維截面,應(yīng)力乘以鋼管纖維對(duì)應(yīng)面積,應(yīng)變乘以鋼管等效自由變形長(zhǎng)度Le;對(duì)于混凝土纖維,應(yīng)力乘以混凝土纖維對(duì)應(yīng)面積,應(yīng)變乘以鋼管屈曲高度Lb,得各自力-位移關(guān)系。

此外,承插連接橋墩鋼管在往復(fù)加載過程時(shí)發(fā)生局部屈曲后,還會(huì)在屈曲鼓出位置發(fā)生撕裂,如圖4(b)所示。在有限元模型中,鋼管的撕裂同樣通過應(yīng)力下降的方式予以考慮,如圖5第一象限所示,假設(shè)當(dāng)鋼管纖維應(yīng)變大于撕裂應(yīng)變?chǔ)舤時(shí),應(yīng)力降為0,其中,εt取為極限拉應(yīng)變?chǔ)舥的2/3,以考慮鋼管受低周疲勞荷載作用。此處需要說(shuō)明的是,后續(xù)分析只將εt作為結(jié)構(gòu)損傷的判斷依據(jù),對(duì)橋墩鋼管撕裂后的性能不作研究。

2.2 混合連接橋墩模型

對(duì)于混合連接鋼管混凝土橋墩,從鋼管與內(nèi)部混凝土協(xié)同工作角度出發(fā),墩身可分為上下兩部分,分別采用不同纖維梁截面單元進(jìn)行模擬。墩身下部截面由于墩底鋼管與承臺(tái)中斷,且鋼管與內(nèi)部核心混凝土存在連接滑移,因此,鋼管不承受縱向拉、壓應(yīng)力,僅對(duì)混凝土起約束作用,故墩身下部單元截面的纖維劃分不考慮鋼管,如圖6(c)所示。而墩身上部混凝土和鋼管共同作用,其截面纖維劃分需包含完整的鋼管與混凝土纖維,如圖6(b)所示。此外,墩身纖維截面的核心混凝土采用Mander提出的約束混凝土本構(gòu)模型,鋼管采用鋼材彈塑性滯回本構(gòu)模型,而預(yù)應(yīng)力筋的模擬與承插連接鋼管混凝土橋墩相同。

圖6 HC橋墩有限元模型示意圖Fig.6 Details of HC column finite element model

耗能鋼筋由桿單元模擬,長(zhǎng)度為無(wú)黏結(jié)加上兩端等效黏結(jié)滑移長(zhǎng)度leu以模擬耗能鋼筋應(yīng)變滲透的影響。其中,leu采用Palermo等[28]給出的公式計(jì)算

leu=0.022dsfy

(4)

LP=0.08L+0.022dsfy

(5)

式中,L為橋墩高度(m)。由于接觸面不能承受拉應(yīng)力,接觸彈簧抗拉強(qiáng)度取為0。

2.3 擬靜力試驗(yàn)驗(yàn)證

為了驗(yàn)證上述兩種橋墩數(shù)值模型的有效性,本文利用文獻(xiàn)[30]的試驗(yàn)結(jié)果進(jìn)行擬合。試件為兩個(gè)1/4.75縮尺比的橋墩模型,模型設(shè)計(jì)和主要尺寸如圖7所示。 承插連接鋼管混凝土試件(以下簡(jiǎn)稱SC試件)與混合連接鋼管混凝土試件(以下簡(jiǎn)稱HC試件)的橋墩凈高均為1.75 m,計(jì)算高度為2 m(承臺(tái)上表面至加載點(diǎn)的高度);橋墩直徑0.44 m,鋼管壁厚度為4 mm,內(nèi)部填充C50核心混凝土,墩身中心線埋設(shè)聚乙烯管作為預(yù)應(yīng)力孔道,直徑70 mm。恒載軸壓比為7%,預(yù)應(yīng)力軸壓比為10%。SC試件的等效縱筋配筋率與HC試件縱筋配筋率均為3.6%。擬靜力試驗(yàn)采用力-位移混合控制的加載制度,鋼管或耗能鋼筋屈服前采用力控制,屈服后變?yōu)槲灰瓶刂?每一級(jí)加載進(jìn)行3次往復(fù)循環(huán)。

(a) 試件尺寸

(b) 承插連接(SC)

(c) 混合連接(HC)圖7 試件設(shè)計(jì)圖(mm)Fig.7 Geometry of column specimens (mm)

根據(jù)本文第2章的模擬方法建立SC和HC試件有限元模型,對(duì)其進(jìn)行往復(fù)推拉分析得到數(shù)值分析力-漂移比關(guān)系曲線,并與試驗(yàn)結(jié)果進(jìn)行對(duì)比,兩試件的各種響應(yīng)對(duì)比結(jié)果如圖8所示。由圖8可知,有限元的各種模擬結(jié)果與試驗(yàn)數(shù)據(jù)基本吻合,表明了纖維模型能夠較好地模擬出滯回荷載下,SC試件因鋼管屈曲、屈曲后撕裂和鋼管與承臺(tái)混凝土黏結(jié)滑移,以及HC試件接縫搖擺的力學(xué)行為對(duì)其力-漂移比關(guān)系的影響。

(a) SC試件滯回曲線

(b) HC試件滯回曲線

(c) 骨架曲線

(d) 殘余位移比

(e) 等效阻尼比圖8 數(shù)值計(jì)算結(jié)果與試驗(yàn)數(shù)據(jù)比較Fig.8 Comparisons between numerical calculation results and experimental data

具體對(duì)比而言,兩試件的有限元模型能很好的捕捉到各自承載力-漂移率關(guān)系的骨架曲線如圖8(c)所示,在5.2%漂移率時(shí),SC和HC試件有限元模型分析預(yù)測(cè)出承載力為247.8 kN和315.8 kN,與對(duì)應(yīng)試驗(yàn)結(jié)果誤差分別為6.0%和3.3%。對(duì)于與自復(fù)位能力有關(guān)的殘余位移比δra,有限元模型也能做出合理的預(yù)測(cè)。圖8(d)給出了兩試件殘余位移比δra的試驗(yàn)和數(shù)值對(duì)比結(jié)果,其中δra定義為某加載等級(jí)下的殘余位移與加載位移的比值,按下式計(jì)算

(6)

式中:δre為殘余位移;δim為加載位移。對(duì)于SC試件,在加載漂移比在1.5%～4.5%區(qū)間內(nèi),數(shù)值和試驗(yàn)的殘余位移吻合度較好;而漂移比大于4.5%后,數(shù)值計(jì)算的結(jié)果偏小。對(duì)于HC試件,δra的數(shù)值計(jì)算結(jié)果在所有漂移率下均略小于試驗(yàn)結(jié)果(約10%),但整體增長(zhǎng)較趨勢(shì)一致。兩試件的殘余狀態(tài)模擬結(jié)果偏小的主要原因是有限元模型中的鋼管或耗能鋼筋未考慮累計(jì)損傷的影響,減小了對(duì)殘余位移的貢獻(xiàn),且混凝土進(jìn)入塑性后的高度非線性也影響殘余狀態(tài)的預(yù)測(cè)。圖8(e)給出了有限元模型對(duì)于等效阻尼比的預(yù)測(cè)結(jié)果,其中ξeq按下式計(jì)算

(7)

式中,Ed和Es分別為每一圈滯回環(huán)耗散的能量以及儲(chǔ)存的彈性應(yīng)變能。由圖8可知,SC試件有限元在漂移比大于1%時(shí),與試驗(yàn)的等效阻尼比結(jié)果吻合效果較好;而對(duì)于HC試件,采用有限元分析會(huì)一直略低估其耗能能力,即數(shù)值結(jié)果略小于試驗(yàn)結(jié)果(約3%)。

綜上對(duì)比分析可見,所建立的數(shù)值模型能表征出兩種橋墩的滯回響應(yīng),滿足后續(xù)章節(jié)進(jìn)行橋梁動(dòng)力分析所需的精度要求。

3 鋼管混凝土橋墩橋梁地震反應(yīng)特點(diǎn)

本章以一座4跨連續(xù)梁橋?yàn)檠芯繉?duì)象,其橋型尺寸如圖9所示。每跨跨度為30 m,縱橋向,3#墩為固定墩,采用固定支座,其余橋墩為活動(dòng)墩,采用球鋼支座;橫向固結(jié)。主梁采用預(yù)應(yīng)力小箱梁,一期恒載為19.3 t/m,二期恒載為6.11 t/m,下部結(jié)構(gòu)為鋼管混凝土獨(dú)柱墩以及承臺(tái)樁基礎(chǔ),墩高8 m,直徑1.6 m,鋼管壁厚1.6 cm。橋墩自重軸壓比約為8%,預(yù)應(yīng)力筋配筋率為0.6%,預(yù)應(yīng)力軸壓比為10%。

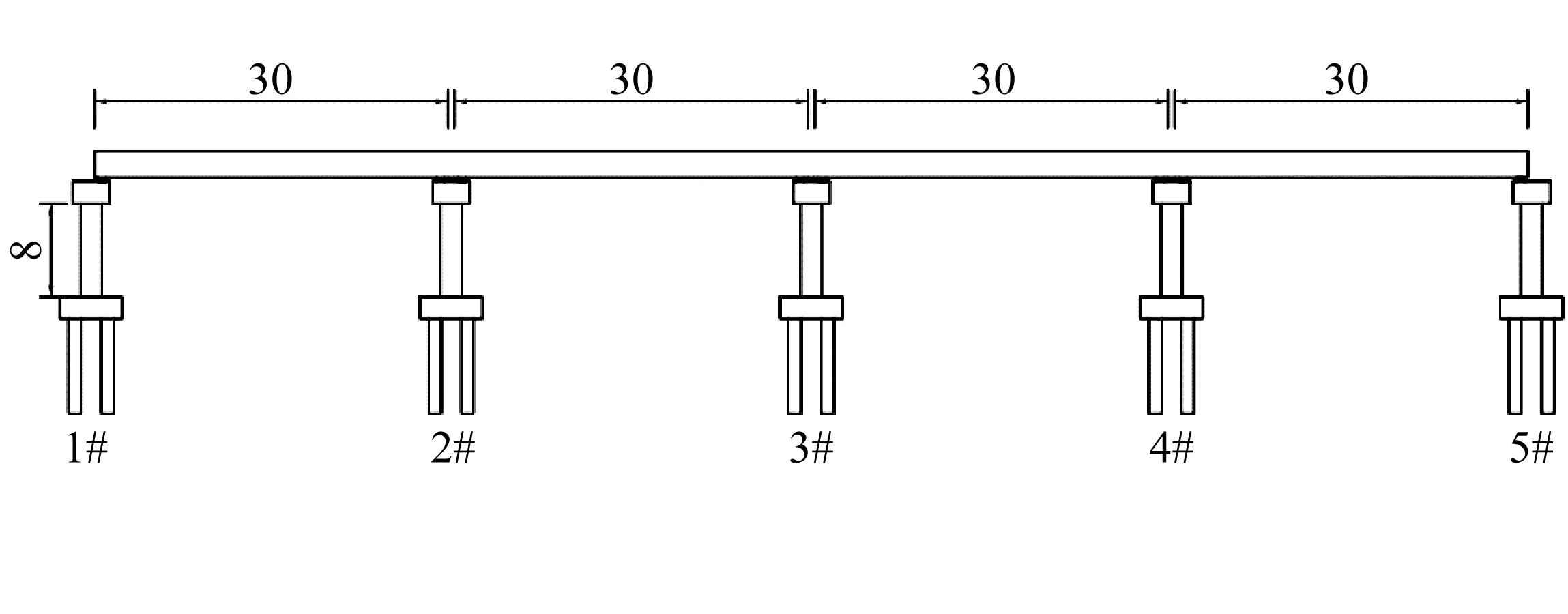
圖9 橋型布置圖(m)Fig.9 Prototype bridge overview (m)

為了比較插承式連接鋼管混凝土橋墩橋梁和混合連接鋼管混凝土橋梁墩橋梁的地震反應(yīng)特點(diǎn),以圖9所示的橋梁為背景,分別考慮以下三種橋墩工況:① 采用插承連接預(yù)應(yīng)力鋼管混凝土橋墩(以下簡(jiǎn)稱SC橋墩);② 采用混合連接預(yù)應(yīng)力鋼管混凝土橋墩(以下簡(jiǎn)稱HC橋墩);③ 采用無(wú)預(yù)應(yīng)力承插連接鋼管混凝土橋墩(以下簡(jiǎn)稱SCP0橋墩),建立上述三種工況下橋梁的空間動(dòng)力模型。三種工況橋墩的截面尺寸、高度以及鋼管壁厚度均相同。SC、SCP0橋墩承插深度為1.5 m,鋼管對(duì)應(yīng)的等效縱筋配筋率為4%;HC橋墩墩底接縫截面耗能鋼筋布置為64φ40,配筋率與SC和SCP0橋墩等效縱筋配筋率相等,約為4.0%。

采用非線性分析軟件OpenSees建立橋梁空間有限元模型,如圖10所示。主梁和蓋梁均為C50混凝土澆筑,在地震中保持彈性,采用線彈性單元模擬。橋墩采用C50混凝土以及q235鋼管材料,SC和HC橋墩采用彈塑性纖維單元模擬,具體模擬方法以及采用的混凝土與鋼材料本構(gòu)與第2章介紹的橋墩數(shù)值模型模擬方法相同。SCP0橋墩模型通過將SC橋墩模型預(yù)應(yīng)力筋面積取為0得到。對(duì)于固定支座,固定方向采用主從約束模擬,活動(dòng)支座采用雙線性理想彈塑性彈簧單元模擬,摩擦因數(shù)取0.03[31]。

圖10 橋梁有限元模型示意圖Fig.10 Bridge finite element model overview

從美國(guó)太平洋地震研究中心選取10條地震中實(shí)際記錄的遠(yuǎn)場(chǎng)(斷層距Rrup>90 km)地震動(dòng)作為地震動(dòng)輸入,其特征如表1所示。10條地震動(dòng)PGA調(diào)為0.2g后繪制其加速度反應(yīng)譜及其均值譜如圖11所示。

表1 地震動(dòng)時(shí)程特征Tab.1 Ground motions’characteristics

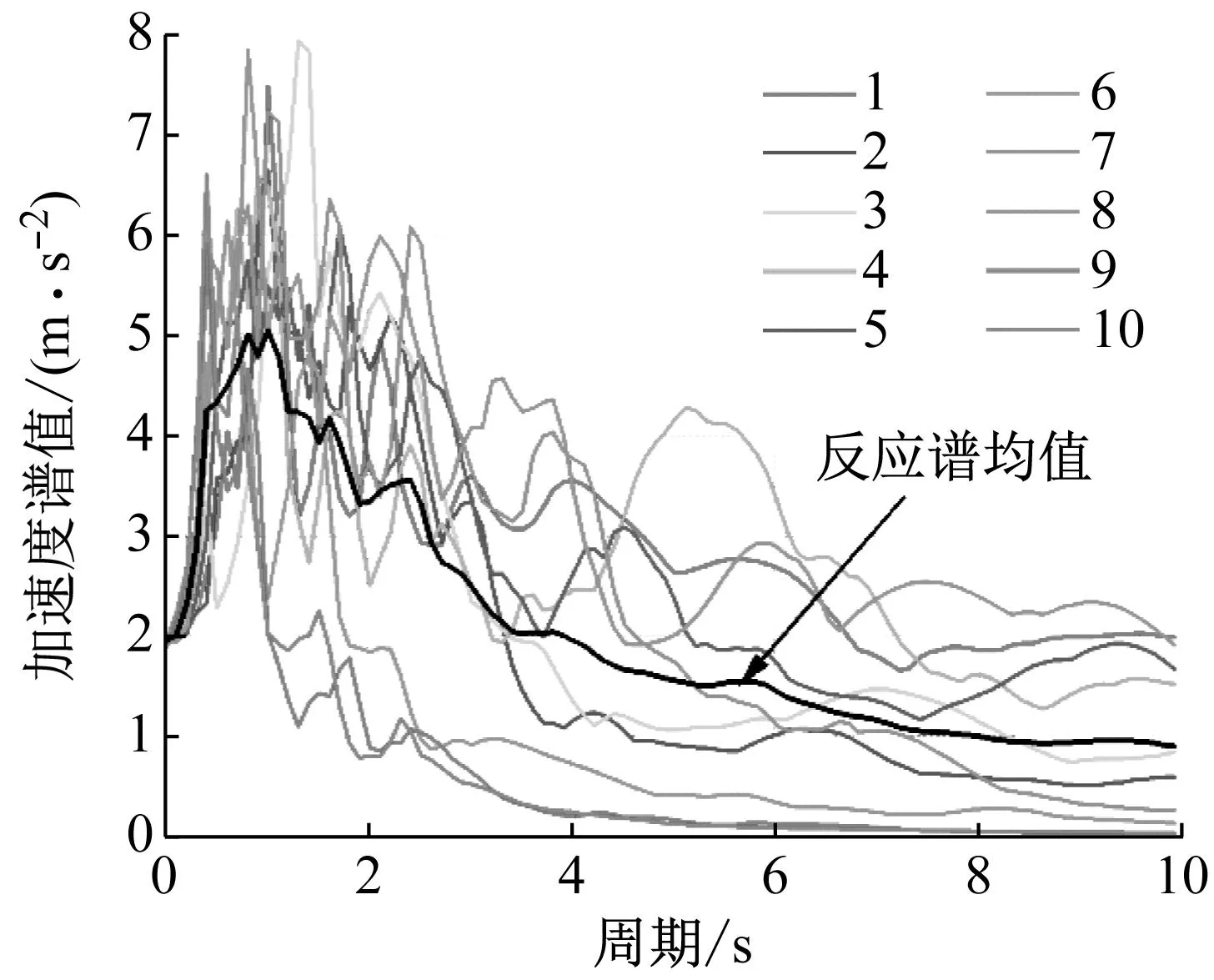
圖11 地震動(dòng)加速度反應(yīng)譜Fig.11 Acceleration response spectrum

對(duì)SC、HC和SCP0三種形式的單墩進(jìn)行橫向Pushover分析,得到主要損傷狀態(tài)與漂移比關(guān)系如表2所示。表中的極限漂移比定義為鋼管撕裂、耗能鋼筋拉斷、預(yù)應(yīng)筋屈服或核心混凝土壓碎對(duì)應(yīng)的漂移比。由表可知當(dāng)漂移比小于1%時(shí),三種橋墩均處于線彈性范圍;而SC與SCP0橋墩在漂移比為2%左右發(fā)生鋼管屈曲。

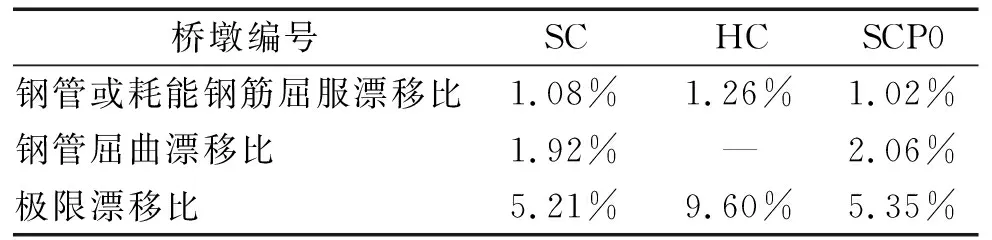
表2 橋墩損傷狀態(tài)與漂移比對(duì)應(yīng)關(guān)系Tab.2 Relationships between damage status and drift ratio

將PGA分別調(diào)幅至0.1g～0.8g,作為結(jié)構(gòu)的“橫橋向”地震動(dòng)輸入。初步分析可以表明,2#墩橫橋向地震響應(yīng)最大,故選取2#墩響應(yīng)結(jié)果進(jìn)行結(jié)果討論。圖12(a)給出了橋梁分別采用SC、HC和SCP0橋墩時(shí),2#墩的最大漂移率均值隨PGA的變化情況。由圖12可知,當(dāng)PGA < 0.2g時(shí),三種橋墩的最大漂移率均小于1%,由表2可知,此時(shí),三種橋墩鋼管或耗能鋼筋均未屈服,結(jié)構(gòu)保持彈性。因彈性階段,墩頂最大位移主要取決于結(jié)構(gòu)的初始剛度,而三條曲線幾乎重合,表明三種橋墩具有接近的初始剛度。

(a) 最大漂移比

(b) 殘余漂移比圖12 地震響應(yīng)平均值隨PGA變化曲線Fig.12 Average seismic responses curves

當(dāng)PGA達(dá)到0.2g～0.4g時(shí),SC和SCP0橋墩鋼管最先屈服,而HC橋墩耗能鋼筋也在PGA超過0.3g時(shí)屈服(圖12(a)中圓形標(biāo)記),三個(gè)橋墩均進(jìn)入塑性階段,且漂移率響應(yīng)較一致。此時(shí)橋墩最大漂移比主要依賴于墩身屈后剛度與滯回耗能。由于此時(shí),SC和SCP0橋墩尚未發(fā)生鋼管屈曲,鋼管等效縱筋配筋率與HC橋墩耗能鋼筋配筋率也相等,可認(rèn)為該階段三種橋墩的耗能能力和屈后剛度差異小。

當(dāng)PGA在0.4g～0.6g區(qū)間時(shí),SC和SCP0橋墩分別在0.40g和0.43g時(shí),發(fā)生鋼管屈曲(圖12(a)中方形標(biāo)記),結(jié)構(gòu)剛度以及耗能能力下降。SC橋墩中的預(yù)應(yīng)力筋會(huì)增加鋼管受壓側(cè)的應(yīng)力,使SC橋墩略先于SCP0橋墩發(fā)生屈曲,引起剛度以及滯回能力更早退化,響應(yīng)位移響應(yīng)增大,當(dāng)PGA = 0.6g時(shí),SC橋墩最大漂移率較SCP0和HC分別大15%和33%。此外,鋼管屈曲導(dǎo)致結(jié)構(gòu)受力性能差異逐漸明顯,其中,HC橋墩墩身未屈曲,位移響應(yīng)較小,表明結(jié)構(gòu)仍保持足夠的屈后剛度。

當(dāng)PGA>0.6g時(shí),圖12(a)中的SCP0橋墩對(duì)應(yīng)的曲線出現(xiàn)明顯拐點(diǎn),這是由于SCP0未有預(yù)應(yīng)力筋,鋼管屈曲后不能提供充足剛度,結(jié)構(gòu)承載力瞬間進(jìn)入下降段。在PGA為0.8g時(shí),兩橋墩均已達(dá)到極限漂移比,鋼管發(fā)生撕裂,且SCP0橋墩最大位移響應(yīng)超過SC橋墩;HC橋墩具有良好的塑性變形能力,在PGA為0.8g時(shí)仍未達(dá)到鋼筋斷裂極限漂移比,仍為結(jié)構(gòu)提供滿意的耗能能力,使HC橋墩漂移比遠(yuǎn)小于SC和SCP0橋墩。

圖12(b)給出了橋梁分別采用SC、HC和SCP0橋墩時(shí),2#墩的殘余漂移比均值隨PGA的變化。圖中可以看出,PGA<0.3g時(shí),三種橋墩殘余位移均小于0.1%,可忽略不計(jì)。而當(dāng)PGA增大到0.4g時(shí),三種橋墩震后殘余漂移比大小關(guān)系為:SC>SCP0>HC。由前面的分析可知,此時(shí),SC和SCP0橋墩鋼管開始發(fā)生屈曲,略微減小了橋墩自復(fù)位的能力。不過,總體而言,當(dāng)PGA < 0.5g時(shí),SC和SCP0橋墩殘余位移差異較小,表明是否采用預(yù)應(yīng)力對(duì)承插式橋墩的自復(fù)位能力影響不大。

當(dāng)PGA增大到0.5g以上時(shí),三種橋墩震后殘余漂移比關(guān)系變化為:SCP0 > SC > HC。可見,因?yàn)镾CP0橋墩沒有預(yù)應(yīng)力筋,只依靠上部結(jié)構(gòu)重力提供少量自復(fù)位趨勢(shì)不足以使橋墩擁有優(yōu)異的自復(fù)位性能,且隨著墩頂水平位移增大,重力易轉(zhuǎn)變?yōu)閮A覆力矩;相比而已,SC橋墩中預(yù)應(yīng)力筋提供的自復(fù)位能力,會(huì)隨著水平位移增大而逐步明顯。HC橋墩的搖擺機(jī)同樣能為其提供滿意的自復(fù)位能力,殘余漂移率均小于0.2%。

圖13給出了橋梁分別采用SC、HC和SCP0橋墩時(shí),2#墩在1號(hào)地震動(dòng)(分別將PGA = 0.1g、0.4g和0.7g)橫橋向輸入下的位移時(shí)程曲線。當(dāng)PGA = 0.1g時(shí),三種橋墩時(shí)程曲線幾乎一致,且無(wú)明顯殘余位移證實(shí)了結(jié)構(gòu)處在彈性范圍且剛度較接近。當(dāng)PGA = 0.4g時(shí),HC橋墩位移時(shí)程曲線仍與PGA = 0.1g時(shí)相似;SCP0橋墩尚未達(dá)到屈曲漂移比(1.26%,表2),殘余位移較小,約為0.4%;但SC橋墩在38 s時(shí),漂移比接近2%,鋼管發(fā)生屈曲,此后,漂移率響應(yīng)逐漸負(fù)向偏移,產(chǎn)生較明顯的殘余位移(約0.9%)。當(dāng)PGA = 0.7g時(shí),SC和SCP0橋墩發(fā)生較大損傷,在40 s時(shí),時(shí)程曲線波峰波谷出現(xiàn)的頻率降低,表明結(jié)構(gòu)剛度退化明顯,響應(yīng)結(jié)束后的殘余位移分別達(dá)到了2.0%和3.9%;HC橋墩位移曲線形狀與小震(PGA = 0.1/0.4g)時(shí)相比,無(wú)明顯變化,保持良好的抗震性能。

圖13 橋墩漂移比時(shí)程曲線Fig.13 Drift ratio time history curve

通過以上分析比較,對(duì)SC、HC和SCP0橋墩橋梁地震反應(yīng)特點(diǎn)總結(jié)如下:① HC橋墩的搖擺機(jī)制提供了良好的自復(fù)位能力,地震下橋梁結(jié)構(gòu)的殘余位移較小,屬于低損傷結(jié)構(gòu);② SC橋墩中的預(yù)應(yīng)力筋易引起鋼管更早屈曲,弱化結(jié)構(gòu)的自復(fù)位性能,在PGA = 0.4g時(shí),其殘余位移在三種橋墩中最大,但預(yù)應(yīng)力筋可為橋墩提供自復(fù)位能力,在PGA > 0.5g時(shí),有效減小殘余位移;③ 不設(shè)置預(yù)應(yīng)力筋的SCP0橋墩,僅由上部結(jié)構(gòu)自重提供自復(fù)位趨勢(shì),在地震PGA > 0.5g時(shí),產(chǎn)生了最大的殘余位移。

4 結(jié) 論

本文以承插連接和混合連接兩種連接形式的預(yù)應(yīng)力節(jié)段拼裝鋼管混凝土橋墩為研究對(duì)象,進(jìn)行了數(shù)值模擬研究,結(jié)合一座4跨連續(xù)梁橋進(jìn)行非線性動(dòng)力分析,得出如下結(jié)論:

(1) 承插連接橋墩震后損傷表現(xiàn)為鋼管受壓屈曲和受拉撕裂,且發(fā)生屈曲后,橋墩耗能能力、結(jié)構(gòu)剛度和自復(fù)位能力明顯下降,表明有限元數(shù)值分析時(shí)應(yīng)考慮鋼管屈曲的影響;而混合連接鋼管混凝土橋墩的震后損傷表現(xiàn)為墩底接縫擠壓破壞,因此,數(shù)值分析需模擬出搖擺接縫張開后的搖擺行為。

(2) 建立的考慮承插連接橋墩鋼管受壓屈曲和受拉撕裂、混合連接鋼管混凝土橋墩墩底接縫搖擺效應(yīng)的有限元模型能較好地再現(xiàn)出承插連接鋼管混凝土橋墩和混合連接鋼管混凝土橋墩的側(cè)向力-漂移率曲線、滯回耗能和殘余位移等響應(yīng),可作為橋梁結(jié)構(gòu)動(dòng)力響應(yīng)計(jì)算的分析模型。

(3) 強(qiáng)震作用下(PGA >0.4g),混合連接鋼管混凝土橋墩性能優(yōu)于承插連接橋墩,而在中小地震作用時(shí)(PGA ≤ 0.4g),兩者性能無(wú)明顯差異。強(qiáng)震時(shí),承插連接橋墩發(fā)生鋼管屈曲,性能迅速退化,殘余位移明顯增大,在PGA = 0.8g時(shí),殘余漂移比大于4%,而混合連接橋墩因搖擺特性,能一直保持良好的自復(fù)位性能,殘余位移小于0.2%。

(4) 與無(wú)預(yù)應(yīng)力承插連接橋墩相比,預(yù)應(yīng)力承插連接橋墩具有較強(qiáng)的自復(fù)位能力。在PGA < 0.5g時(shí),采用預(yù)應(yīng)力與否對(duì)承插連接橋梁的地震響應(yīng)影響不大,但當(dāng)PGA大于0.6g時(shí),預(yù)應(yīng)力的使用能夠有效減小殘余位移,減小殘余位移約38%。總體來(lái)看,采用預(yù)應(yīng)力能夠改善承插連接鋼管混凝土橋墩的抗震性能,但需注意,雖然本文所選研究對(duì)象為量大面廣的連續(xù)梁橋,但針對(duì)不同設(shè)計(jì)參數(shù)下,兩種連接形式的橋墩及其橋梁抗震性能,仍需進(jìn)一步探索,以擴(kuò)展本文研究適用范圍。