“倍”的意義不僅是除法運算的結果

齊美 郜舒竹

【摘? ?要】我國小學數學課程在教學中將“倍”理解為除法運算的結果。通過對文獻的考察發(fā)現，“倍”具有關系和運算兩種意義。從皮爾斯符號學產生意義的角度來看，指示物、符號與解釋項三個要素密切相關。對“倍”的理解依賴于個體經驗與具身操作，而非機械模仿、簡單計算。因而進一步提出，在數學課程設計與教學中，應綜合“倍是關系”與“倍是運算”兩種意義，使學生對“倍”的理解更加全面。

【關鍵詞】倍的認識；關系；意義

“倍”作為小學數學課程的重要內容，在我國小學數學教科書中通常安排在除法之后進行教學。人教版教材三年級上冊中關于“倍”的描述是“求擦桌椅的人數是掃地的幾倍，就是求12里面有幾個4，用除法計算”。這樣的描述將“倍”視為運算的結果，將運算的對象指向“數”，運算的過程等同于“除法”，這或許就是將“倍的認識”安排在整數除法之后進行教學的原因。按照這樣的認識，“6÷3=2”與“6是3的2倍”僅是在名稱上發(fā)生了變化，即將除法的結果“商”改為“倍”，從而引發(fā)教學的困惑：既然已經有了除法，為什么還需要學“倍”？“倍”有什么意義？

一、文獻考察

在漢語中，“倍”有增加之意，與“半”相對。成語“事半功倍”用來形容花費的氣力小，收到的成效大。與之相反，“事倍功半”則用來形容花費的氣力大，收到的成效小。如果用“事一功一”作為參照，“事半功倍”的“半”表示二分之一，而“倍”則表示二，意味著在原數基礎上增加相同的數量。歷史上，人們早已熟練掌握“加倍”的運算方法，如《孫子算經》中的雞兔同籠問題就提及了“倍足法”。“加倍”用現在的算術語言來說就是“乘2”的意思［1］，同理，諸如“3倍、4倍”大多是“原數乘3、乘4”之意。

在西方，關于“倍”的概念被描述為倍量（Multiple）。古希臘歐幾里得《原本》（Elements）第五卷中對倍量的闡述是：較小量是較大量的一部分（Part），當一個較大量能被較小量完全測量時，這個較大量就是較小量的倍量。［2］由此可見，倍量概念源于測量，用于描述較大量與較小量之間的數量關系。在用法上，倍量與比密切相關：把一個量幾倍以后等于另外一個量，就說這兩個量彼此之間有一個比。［3］119清代李善蘭所譯的《幾何原本》中對“倍”的表述是：分者數之數小能度大以小為大之一分，諸分者小數度大數而有奇零不盡以小為大之幾分，若小數能度大者則大為小之幾倍。

從這里可以看出，《幾何原本》中的“量”在文言文譯本中表達為“數”，失去了原有“形”的意義。在現代的中譯本《歐幾里得·幾何原本》中，根據語境，倍量有時會被翻譯為倍數，即用較小量測量較大量的次數稱為倍數；同倍量（Equimultiples）翻譯為相等的倍數，用以描述兩組不同的較大量與較小量之間倍數相同的關系。［3］119

通過對古今中外文獻進行梳理，發(fā)現“倍”具有“關系”和“運算”兩種意義。在我國各個版本教材中，1960年前的教材對“倍”含義的呈現注意到了關系，但表達形式指向運算的結果。隨著時間的推移，后續(xù)版本的教材便更多指向運算的結果而忽視了本質的表達，這可能是導致人們將“倍”誤解為運算結果的原因。

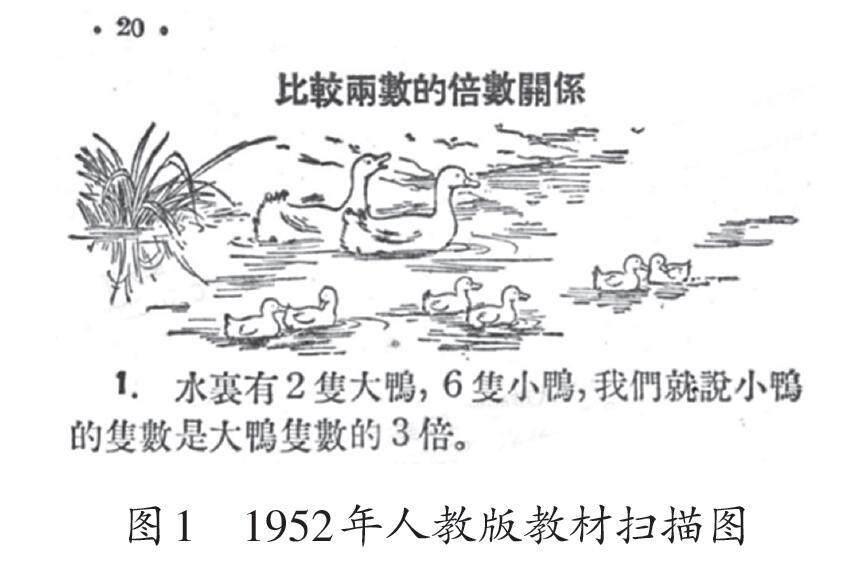
1906年，由日本數學家樺正董原著，趙繚、余煥東翻譯的《新譯算術教科書》借助單位的度量表示“倍”，包含幾個這樣的單位就是幾倍，即“計量之大小多寡等相當于單位之幾倍或幾分皆謂之數”。在人民教育出版社1952年出版的十年制小學課本《算術（第六冊）》中，“倍的含義”是通過數量與數量之間的關系引出的：水里有2只大鴨，6只小鴨，我們就說小鴨的只數是大鴨只數的3倍（如圖1）。然而，對于“倍”這一概念，教材并未給出明確的定義。

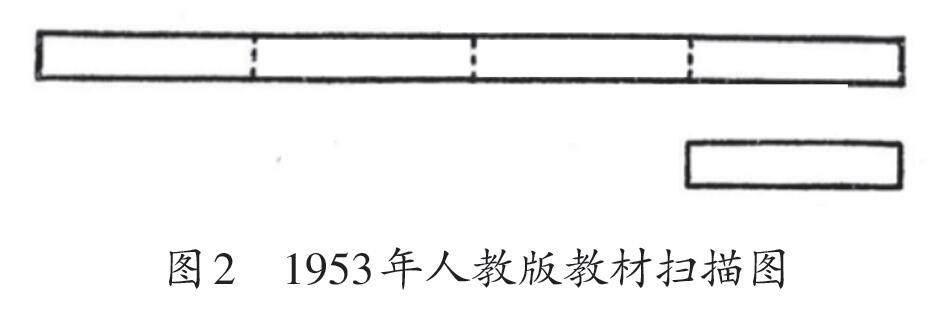
在人民教育出版社1953年出版的初級小學課本《算術（第五冊）》中，“倍的含義”是用幾何量之間的關系來表征的。即照圖2剪兩張紙條，拿短紙條去量長紙條，看長紙條里包含幾個短紙條。長紙條包含4個短紙條就說長紙條是短紙條的4倍，反過來說就是短紙條是長紙條的四分之一。

但在對“倍”進行概念描述時，教材采用了除法計算的方式：比較兩數的倍數關系時，先拿小數去除大數，得數是幾，大數就是小數的幾倍；反過來說，小數就是大數的幾分之一。

人民教育出版社1960年出版的初級小學課本《算術（第四冊）》直接將“倍”的概念描述為倍是運算的結果：“求一個數的幾倍是多少，就用幾乘這個數。”2001年版及以后的版本也都大同小異，均強調“倍”是一種運算的結果，而相對忽略其描述關系的本質屬性。

相較于國內來說，國外教材的呈現方式就比較重視“倍”是一種關系、一種模型（Model）。2014年版新加坡教材Visible Thinking in Mathematics 2A將“倍”視為運算模型，對加減乘除進行綜合運用。為加深理解，教材提供了3個例題進行辨析，并輔之以3個圖示，要求學生根據問題類型進行連線匹配。

問題1：艾瑪有20枚胸針，靜文的胸針數量是艾瑪的3倍，她們一共有多少枚胸針？

問題2：靜文的胸針數量是艾瑪的3倍，靜文比艾瑪多20枚胸針，她們一共有多少枚胸針？

問題3：靜文的胸針數量是艾瑪的3倍，她們一共有20枚胸針，艾瑪有幾枚胸針？［4］

分析上述三個問題可知，問題1與中圖對應，問題2與下圖對應，問題3與上圖對應。每個問題對應的模型不同，解決問題的思維方式也各不相同。學生可通過比較問題描述與圖形表征的差異，提升運算能力。

以問題1為例，新加坡教材原文的描述為：“Jingwen had 3 times as many pins as Emma. Emma had 20 pins. How many pins did they have altogether？”。句子中的“times”，翻譯過來是倍的意思。在英語的表達中，“times”也有乘法的含義。“2×3”就是“2 times 3”，次數在前，被乘的數在后，表示“3出現了2次”。而“times”就是重復出現的次數，即選定單位量后，重復出現幾次就是幾倍。這與我國《新譯算術教科書》中通過單位的度量表示倍的概念是一致的，即包含幾個這樣的單位就是幾倍。

綜上所述，倍這個概念起源于測量，用于描述用較小量來測量較大量時兩者之間的關系。在用法上，它可以用來比較部分與整體的關系、同一對象變化前后的關系以及兩組不同對象之間的關系。其共同的特點就是標量關系（Scalar Relationship），即把標準量看作“單位一”去度量比較量，比較量有幾個這樣的單位就是幾倍。［5］在比較的過程中，常用除法和乘法的形式來進行運算，但各版本的教科書在呈現形式上還停留在不同對象之間的比較。事實上，“倍”的含義和應用遠不止于此。

二、意義形成

“倍”作為一個數學術語，是通過對客觀事物進行抽象所形成的“概念（Concept）”，是人的“心智（Mind）”中自內而外的主觀“生成（Poietic）”。［6］對“倍”的理解依賴于個體經驗與具身操作。杜威說：“理解就是要掌握其意義。”［7］那么，如何抓住意義呢？有意義的情境必須包含三個要素：一是指示物 （Referent），如事件、物品、動作等；二是指示物的符號（Symbol）；三是獨特的解釋（Interpret）。［8］

符號產生的意義依托于個體原有的經驗，即當符號出現時，會喚起個體過去的經歷或頭腦中形成的想象。由于經驗不同，學生在頭腦中會形成不同的圖式，隨之也就會產生不同的意義。以算式3×2=6為例，假設學生尚未學習乘法，3×2=6只不過是一些符號的堆砌，毫無意義。而隨著學習經驗的累加，學生能根據乘法所涉及的量的性質及其之間的關系產生至少三種不同類型的理解：相等群組（Equivalent Groups）、乘法比較（Multiplicative Comparison）和笛卡爾乘積（Cartesian Product）。［9］

在相等群組的類型中，算式3×2=6能夠喚起學生諸如“每個盤子里裝有3個蘋果，有這樣的2個盤子，一共有多少個蘋果？”的經驗，形成如圖4所示的意象圖式。在這個算式中，兩個因數的意義不同，3表示的是每份數，2表示的是份數。那么在這樣的情境中，3×2=6有指示物、符號和個體的解釋，從而使算式具備了具體的意義。

乘法比較這種類型與中文表達的倍數問題大致相同，比較的是一個組與另外一個組（標準組）的關系。3×2=6能喚醒學生頭腦中如圖5所示的意象圖式：第一行有3個小方塊，第二行小方塊的數量是第一行的2倍，第二行小方塊的數量有幾個？其中，3代表的是單位量，2倍指向關系即包含2個3。那么，3×2=6在這樣的情境下就形成了有意義的理解。

在笛卡爾乘積類型中有這樣的情境：一家漢堡店出售單層夾心漢堡，它有3種肉類（香腸、雞肉和牛肉）和2種醬（番茄醬和沙拉醬）。用3×2=6可以表示能買到6種不同口味的單層漢堡。具體來說，3表示3種肉類，2表示的是2種醬料，6代表這2種醬料與3種肉類搭配后有6種不同的情況（如表1）。

因此，學生在進行有意義的學習的過程中，不僅要掌握符號的意義與運算的法則，更要了解符號背后所蘊含的現實意義與價值。不僅要知其然，更要知其所以然，將個體經驗與符號表征進行連接，形成自己的意義理解。

在具身活動中，理解算術符號的意義尤為重要，因為算術符號形成的意義往往和具身的行為動作密不可分。如以某種方式將物體進行聚集、劃分以及比較等。算術符號的意義與顯性行為（Overt Acts）相聯結，即以一種特定方式形成的算術指令。以“什么是2倍關系”為例。將一個長方形ABCD先對折再打開（如圖6），對折過程中，長方形ABFE與長方形DCFE重合，得到兩個面積相同的小長方形。整體面積就是其中一個小長方形面積的2倍（也就是部分與整體的2倍關系）。這樣的操作（Operation）使2倍關系可視化，學生在頭腦中就能形成關于2倍關系的意象（Image），這樣的行為就是有意義的活動。那么學生之后再看到2倍，頭腦中就會復現這樣的經歷，自然也就理解了2倍關系的意思。

三、“倍”的意義

“倍”的意義由多個意義單元（Meaning Unit）組成。在符號形成意義的過程中，意義單元是組成意義的基本結構。當指示物和一個意義價值（Meaning Value）聯結，就形成了一個意義單元。［10］隨著時間的推移，指示物常常在不同方面包含并累積若干個意義價值，形成模式（Pattern）。“倍”作為數學符號的意義，由三種不同的意義單元組成，即描述不同指示物之間的關系、描述指示物部分與整體的關系、描述指示物變化前后的關系。

第一種意義單元描述不同指示物之間的關系。如圖7所示，第一行有3個小方塊，第二行有6個小方塊。那么，第二行小方塊的數量就是第一行小方塊數量的2倍。這樣的意義單元描述的是“2倍”的關系，其中指示物是兩行數量不同的小方塊，意義價值就是第二行指示物數量是第一行指示物的2倍。“2倍”關系就是一個符號，而符號往往有2個或以上的對象以及多個解釋項（Interpretant）。［11］因此，若第一行有4個小方塊，第二行有8個小方塊，第二行小方塊的數量也與第一行小方塊的數量形成“2倍”關系。以此類推，若將一種指示物看成“單位一”，而另一個指示物有這樣的幾個“單位一”，那么這兩種不同指示物之間就形成了一定的倍數關系。

第二種意義單元描述指示物部分與整體的關系。以折紙所形成的倍數關系為例。如圖8所示，將一張長方形紙對折1次、2次、3次，每次對折后，初始的整個長方形面積分別是對折后小長方形面積的2倍、4倍、8倍。在這樣的意義單元中，每次對折，“單位一”在不斷變化，但整體不變，所以形成的部分與整體之間的倍數關系也在不斷變化。因此，同一指示物部分與整體之間形成了新的意義價值，從而構建出新的意義單元。

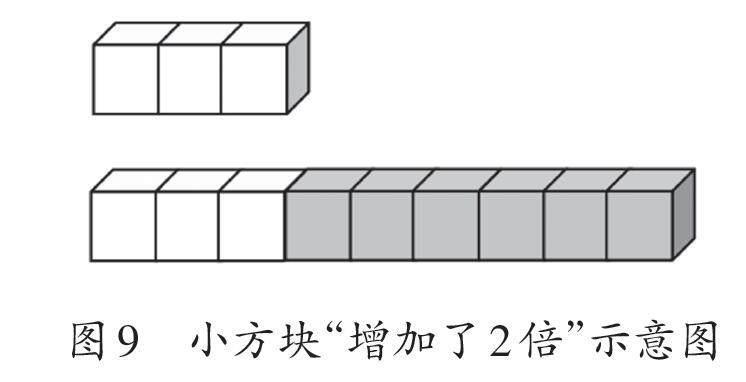
第三種意義單元描述指示物變化前后的關系。在這樣的意義單元中，指示物增加了幾倍，意義價值即在初始狀態(tài)的基礎上增加了幾個這樣的“單位一”。例如，以3個小方塊作為指示物的初始狀態(tài)，這時候的小方塊數量是“單位一”，指令“增加了2倍”即增加2個這樣的“單位一”（如圖9）。那么，變化后的小方塊數量就是初始狀態(tài)+增加量=最終狀態(tài)，即3個“單位一”。因此，“增加了幾倍”闡述變化的增量，意義指向倍數關系的動態(tài)變化。

對“倍”的意義形成的解釋與理解是為了讓教師更清楚“倍”的含義，更好地為學生設計學習活動，讓學生實現對“倍”的理解以及應用。在數學概念的學習中，學生不應停留在簡單的模仿層面，如“幾倍就是乘幾”，而應追求對概念的有意義理解，學會用自己的方式表征數學問題，并理解概念與其他事物之間的關系，以及概念的產生、運作過程、影響和應用的范圍等。實踐研究表明，教師要鼓勵和要求學生進行多元表征，這樣的活動體驗能提升學生靈活解決問題的能力。［12］因此，在教學“倍的認識”時，教師可以參考“倍”的意義的形成過程來設計教學活動，讓學生利用個體經驗和具身操作來實現對倍的理解。

綜上所述，在對“倍”進行課程設計與教學時，簡單地將“倍”定義為“除法計算的結果”并不妥當。為全面呈現“倍”的意義，應當讓學生深入體會倍的運算意義，并深刻認識“倍是關系”。理解“倍”的概念需要依賴于個體經驗與具身操作，需要設計多元表征的學習活動。在小學數學課程中，有諸多關于抽象概念的學習，如分數的認識、小數的認識、分數的意義、小數的意義等。教師應創(chuàng)設有意義的情境，幫助學生通過指示物、符號和個體的解釋形成有意義的理解，并在備課前深入思考“這是什么？學什么？難在哪里？要怎樣做？”這幾個問題。這樣，才能真正落實《義務教育數學課程標準（2022年版）》中關于運算的要求——明晰運算的對象和意義。

參考文獻：

［1］郜舒竹，孫婷婷.加倍取半，算術之源［J］.教學月刊·小學版（數學），2013（7/8）：7-9.

［2］EUCLID. The thirteen books of Euclids elements（Volume Ⅱ）［M］. New York：Dover Publications，1956：126-127.

［3］歐幾里得.歐幾里得·幾何原本［M］.蘭紀正，朱恩寬，譯.西安：陜西科學技術出版社，2003.

［4］WAN A. Visible thinking in mathematics 2A［M］.Singapore：Marshall Cavendish Education，2014：128.

［5］WALLACE A H，GURGANUS S P. Teaching for mastery of multiplication［J］. Teaching children mathematics，2005（1）：26-33.

［6］郜舒竹.釋“比”［J］.教學月刊·小學版（數學），2021（6）：4-8.

［7］DEWEY J. How we think［M］. Boston：D. C. Heath & Co Publishers，1933：137-138.

［8］ENGEN H V. An analysis of meaning in arithmetic. Ⅰ［J］. The elementary school journal，1949，49（6）：321-329.

［9］MULLIGAN J T，MITCHELMORE M C.Young childrens intuitive models of multiplication and division［J］. Journal for research in mathematics education，1997，28（3）：309-330.

［10］KREITLER S. Spheres of meaning［M］.New York：Nova Science Publishers， 2021：16.

［11］皮爾斯.皮爾斯：論符號［M］.趙星植，譯.成都：四川大學出版社，2014：59.

［12］PIEZ C M，VOXMAN M H. Multiple representations：using different perspectives to form a clearer picture［J］. The mathematics teacher，1997，90（2）：164-166.

（首都師范大學初等教育學院）