構建探究式學習模式的初中數學教學

張興良

探究式學習是一種基于學生主動參與、探索的學習方式，它強調學生通過探索、發現并解決問題來構建知識。在數學教學中，探究式學習可以激發學生的學習興趣和動力，提高他們的數學思維能力和問題解決能力。本文以“等腰三角形的性質”教學為例，來探討如何構建探究式學習模式。

一、教學目標

1.了解作為證明基礎的幾條公理，掌握證明的基本步驟和書寫格式。

2.能夠用綜合方法證明等腰三角形的有關性質定理。

3.經歷“探索—發現—猜想—證明”的思想過程，了解證明的意義。

4.形成解決問題的一些基本策略，學會證明的過程，培養證明的應用意識。

5.學會從操作中得出結論，再通過證明，論證得出的結論。

6.形成運用數學思維思考實際問題的習慣。

二、教學重點、難點

重點：經歷“探索—發現—猜想—證明”的過程，證明等腰三角形的有關性質，并能運用性質定理去解決相關的問題。

難點：在證明的過程中發現數學證明的要求及步驟，體會證明的思想。

三、學法建議

學生應重點注意在證明思路和方法上的突破，弄清輔助線的添加及構造；懂得通過圖形的對折、角度的測量、圖形的拼擺等方法探索圖形性質并進行證明的思路的重要性。等腰三角形的性質及結論的證明方法和途徑都不是唯一的；輔助線的添加方法也是多樣的。因此，學生要注意探索證明的不同方法，提倡證明方法的多樣性；要主動參與探索活動，多和同學交流。新課標要求學生在具體情境中學會探索、發現證明的思路，在交流中產生不同的證明方法。學生應采取自主探索、合作交流的學習方式；能聯系生活中的實物，如身邊的建筑物、自然界中的圖形等學習角平分線、等腰三角形的概念和性質。

四、教學過程

（一）提出問題，導入新課

師：在七年級下學期三角形一章的學習中，我們學習了有關三角形全等的幾條公理、定理，同學們還記得嗎？

生1：SSS、SAS、ASA、AAS，還有全等三角形的對應邊相等、對應角相等。

（設計意圖：通過復習前面所學內容，引導學生回憶證明的要求及步驟，以更好的狀態和充足的準備進入新內容的學習。）

（二）應用公理，探求新知

師：在前面的學習中，我們知道SSS、SAS、ASA是公理，不需要證明，是證明其他定理的基本依據，而AAS不是公理，需要證明，同學們能運用公理證明AAS嗎？

學生思考、小組合作交流，請一位同學展示證明過程。

教學分享：

小組合作是探究式學習的重要形式之一。教師可以將學生分成若干小組，鼓勵他們交流和合作共同解決問題。通過小組合作，學生共同探索并學習新知識。

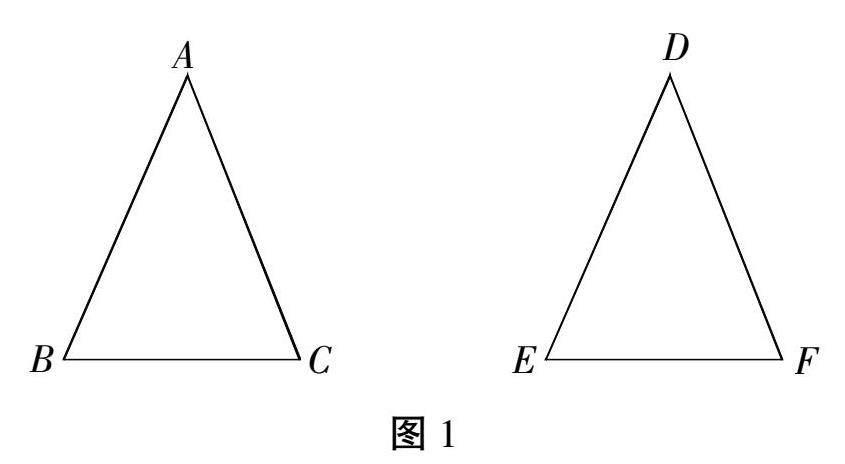
如圖1，已知兩個三角形對應的兩個角相等，且其中一組等角的對邊相等，那么這兩個三角形全等（AAS）。

證明過程：

已知：∠A=∠D，∠B=∠E，BC=EF

求證：△ABC≌△DEF

證明：∵∠A+∠B+∠C=180°

∠D+∠E+∠F=180°（三角形內角和等于180°）

∴∠C=180°-（∠A+∠B），∠F=180°-（∠D+∠E）

又∵∠A=∠D，∠B=∠E（已知）

∴∠C＝∠F

又∵BC=EF（已知）

∴△ABC≌△DEF（ASA）

（設計意圖：設置具體問題，使學生在解決具體問題的過程中學會應用已有知識進行證明，既激發了學生的求知欲，又訓練了學生運用數學的能力；通過讓學生交流討論并動手證明，以此來熟悉證明的基本要求和步驟，為后面的推理證明做準備。）

（三）問題引領，歸納新知

師：等腰三角形除了有兩條邊相等外，它還有哪些性質呢？

生2：將等腰三角形沿著頂角左右對折后，兩邊能完全重合，說明等腰三角形的兩個底角相等。

生3：等腰三角形的兩個底角目測是相等的，所以我用量角器進行了測量，結果表明這兩個角確實相等。

師：同學們通過對折、用量角器測量等方法得出了等腰三角形的兩個底角相等，但結論僅僅靠驗證還不夠。

教學分享：在探究式學習過程中，為了最大限度地挖掘學生自身的潛力，教師可以給學生提供一些學習資源和參考資料，引導他們進行學習和思考。所以，當學生使用對折和量角的方法得出等腰三角形的兩個底角相等時，教師要及時引導學生，結論僅靠驗證還不夠，需要進一步進行邏輯證明。

已知：如圖2，在三角形ABC中，AB=AC

求證：∠B=∠C。

生4：我們前面所學的公理和定理中，SSS、SAS、ASA、AAS，都是在兩個三角形中進行對比得出的結論：兩個三角形的三條邊相等；兩個三角形的兩邊和它們的夾角對應相等；兩個三角形對應的兩邊及夾角相等；兩個三角形的兩角及其中一角對應的邊相等。而在圖2中，只有一個三角形ABC，無法使用上面的公理或定理，結合我們剛才動手操作時將三角形沿頂角對折從而分成兩個全等的三角形，我們可以在進行推理證明時，取線段BC的中點D，然后連接AD，這樣就可以得到兩個全等的三角形ABD和ACD，從而證明等腰三角形的兩個底角相等。以下是具體證明步驟：

證明：取BC的中點D，連接AD

∵AB=AC，BD=CD，AD=AD

∴△ABD≌△ACD（SSS）

∴∠B=∠C（全等三角形的對應角相等）

教師：這位同學通過作線段BC中線的方法得到兩個全等三角形，進而證明等腰三角形的兩個底角相等。除此之外，同學們還有什么別的方法可以證明∠B=∠C。

教學分享：

教師可以根據教學內容和學生的實際情況設計一些啟發性問題，激發學生的思考和興趣。這些問題應具有一定的挑戰性，能夠引導學生進行自主探索和思考。

如，在證明等腰三角形的兩個底角相等時，第一位同學用添加中線的方法進行論證后，教師不是一鼓作氣把剩余內容全部講授完，而是及時提問其他同學還有什么更好的方法，引導學生用前面所學的公理和定理自行推理證明，并進行展示，使學生能夠主動參與到學習過程中。

生5：我們可以作角A的平分線并與線段BC相交于D。連接AD，這樣在三角形ABD和三角形ACD中，AB=AC，∠BAD=∠CAD，AD=AD，根據公理SAS可知三角形ABD和三角形ACD全等。所以，可以得出∠B=∠C。

證明：作角A的平分線并與線段BC相交于D，

∵AB=AC，∠BAD=∠CAD，AD=AD，

∴△ABD≌△ACD（SAS），

∴∠B=∠C（全等三角形的對應角相等）。

生6：可以通過頂點A作底邊BC的垂線AD，在直角三角形ADB和直角三角形ADC中，AB=AC，AD=AD，根據直角三角形中一條斜邊和一條直角邊都對應相等，這兩個三角形就是全等三角形的定理可知，直角三角形ABD和直角三角形ACD全等，所以可得出：∠B=∠C。

證明：通過頂點A作底邊BC的垂線AD，

∵在直角三角形中AB=AC，AD=AD，

∴△ABD≌△ACD（直角三角形中一條斜邊和一條直角邊都對應相等，這兩個三角形就是全等三角形），∴∠B=∠C（全等三角形的對應角相等）。

師：同學們剛才通過作頂角的平分線、作底邊的中線、底邊的高線，用三種不同的方法證明了兩個三角形全等。由此，我們知道了所作的輔線，它既是頂角的平分線，又是底邊的中線和高線。也就是說，我們在用不同的方法在證明等腰三角形兩個底角相等的同時，又得出了等腰三角形的另一個性質：等腰三角形頂角的平分線、底邊上的中線及底邊上的高線互相重合，簡稱“三線合一”。

（設計意圖：讓學生通過多種方法解決同一個問題，提高他們靈活運用知識的能力，同時為得出等腰三角形的另一性質提供鋪墊；讓學生通過猜想、實驗驗證、邏輯證明、總結歸納，使他們對所學知識產生深刻印象；讓學生在運用不同方法進行推理證明的過程中，學會由問題入手，運用所學知識，逐步倒推去解決問題，培養學生的邏輯推斷能力。）

（四）思維拓展，實際應用

師：剛才我們學習了等腰三角形的性質，現在請同學們思考一下，在實際生活中，有哪些地方利用了等腰三角形的這些性質呢？

生7：建筑工人在建房時，為了確定房梁是否水平，常用的方法是把一塊等腰三角板放在梁上，從頂角頂點系一重物，如果系重物的繩剛好經過三角板底邊的中點，就認為房梁是水平的。

師：能說一下理由嗎？

生7：首先，使用的工具是等腰三角板，要想知道是否經過中點，看三角板的刻度就知道了。當重物經過了等腰三角板的中點，那懸掛的線就是底邊的中線。根據三線合一，它也是底邊的垂線，而懸掛的線是鉛垂方向（由物理知識可知，在懸掛的線上掛上重物后，重力的方向是豎直向下的，跟它垂直的房梁就是水平的），所以房梁就是水平的。

生8：江河上的斜拉索橋就是等腰三角形的。只有路兩邊的拉索在長度相等的情況下，才能保證兩邊受力相等，保證橋的受力平衡。

師：同學們的分享很精彩，說明大家不僅掌握了今天所講的知識，還能在平時的生活里用心觀察，能夠運用所學知識去思考問題。希望以后大家能發現更多蘊含在生活中的數學知識，做到學以致用，有所創新。

教學分享：探究式學習強調將數學知識應用到真實的情境和問題中。因此，教師可以設計一些真實的數學問題，讓學生通過探索和解決問題理解數學概念和原理，這樣既能提高學生的學習興趣，也能引導學生將所學知識運用到現實生活中。

五、教學總結

學生可以通過寫日記、小結等方式總結自己的學習經驗和收獲。教師可以提供及時的反饋和評價，幫助學生發現不足并改進學習方法。為了評估探究式學習模式的實施效果，教師可以采用多種評估方法，如觀察學生的學習情況、聽取學生的意見和建議、進行作業和考試等。同時，教師還可以根據學生在探究式學習過程中的表現和成長評估學生的思維能力和問題解決能力。

探究式學習模式是一種有效的學習方式，它可以激發學生的學習興趣和動力，提高學生的數學思維能力和問題解決能力。在探究式學習的實施過程中，教師應注重學生的主動性，真實情境的創建、問題驅動、合作學習的運用，反思和評價的作用，構建探究式學習模式，并不斷改進和完善這一教學模式來提高學生的學習效果和教學質量。

（作者單位：甘肅省榆中縣教學研究室）

編輯：蔚慧敏