平和有乾坤，變化見功力

甄艷

摘要：全面提升高三復習教學與復習備考的整體效益，是高三復習備考中最為重要的一個課題.本文中基于二輪復習，在“三新”背景下，依托“數列”專題，從重視教材、梳理知識、掌握性質、積累經驗等層面來剖析相應的復習建議，為優化復習過程與提升復習效益作了一些嘗試與經驗積累.

關鍵詞：數列；二輪復習；建議；知識；思想

在新課標、新教材、新高考的“三新”背景下，近年全國新高考數學試題的“數列”專題部分，隨著新教學改革理念的逐步深入與延續，更加準確體現高考改革的要求，遵循數學課程標準的教學內容、學業要求和質量標準，以穩定性的考查方式、基礎性的考查要求、全面性的考查內容以及創新性的考查情境等特點，全面突出基礎性，彰顯綜合性，體現應用性，追求創新性，突出數學思想方法性等，合理聚焦數學學科核心素養，體現對數學關鍵能力的考查.

預測今后幾年全國新高考數學試題的“數列”專題部分的考查，還是堅持“四性”，突出“四基”，夯實“四能”.由此，對于該專題的高考二輪復習，必須更有針對性與實用性，本文中從一些復習備考的嘗試與建議入手，拋磚引玉.

1 重視數學教材，打好數學基礎

作為高中課堂教學與學習的基石，教材是主要依據，更是課標標準的實際體現.因而在“數列”專題部分的二輪復習備考中，必須堅持圍繞高中數學教材來展開，充分理解數列的基本概念與基本性質，以及一些相關的典型實例與性質應用等.通過通讀教材，可以再次回顧相關的數學知識與應用場景.

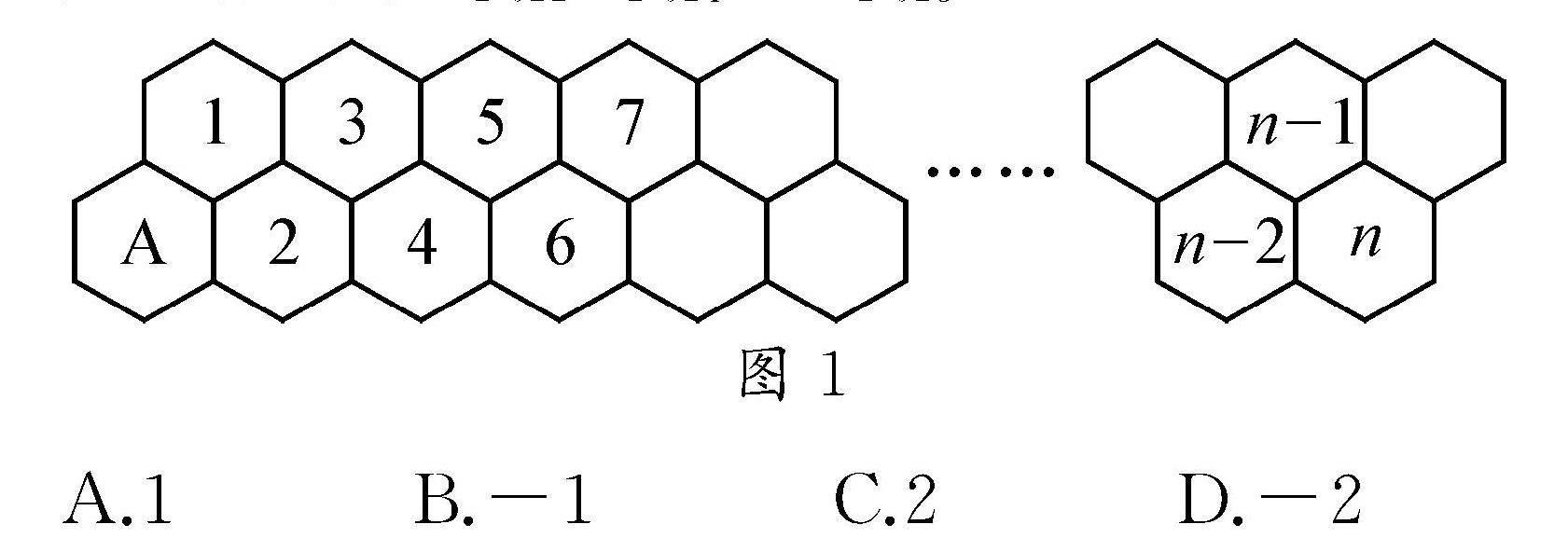
例1? 〔2024屆高三第一次學業質量評價（T8聯考）數學試題〕一只蜜蜂從蜂房A出發向右爬，每次只能爬向右側相鄰的兩個蜂房（如圖1），例如，從蜂房A只能爬到1號或2號蜂房，從1號蜂房只能爬到2號或3號蜂房……以此類推，用an表示蜜蜂爬到n號蜂房的方法數，則a2 022a2 024-a22 023=（? ）.

A.1

B.-1

C.2

D.-2

通過問題場景，借助蜜蜂爬到前若干號蜂房的方法數，合理歸納，構建與之相吻合的斐波那契數列以及對應的數列遞推關系式，借助所求數列項的代數關系式的特征，通過一般性思維與整體思維加以切入，利用等比數列的構建與應用來分析與處理，達到解決創新應用問題的目的.追根溯源，該問題場景源自教材中的“閱讀與思考”欄目：

〔人民教育出版社2019年國家教材委員會專家委員會審核通過的《數學》（選擇性必修第二冊）第四章“數列”第10頁閱讀與思考——斐波那契數列〕

如果用Fn表示第n個月的兔子的總對數，其中F1=1，F2=1，F3=2，可以看出Fn=Fn-1+Fn-2（n∈N*，n>2）.這是一個由遞推公式給出的數列，稱為斐波那契數列.

依托教材“閱讀與思考”欄目的閱讀材料，斐波那契數列一直是數列模塊知識中最為常用的一種基本模型，也是全面考查數列模塊“四基”與關鍵能力等最為重要的一個創新應用場景，備受各方關注.

在“數列”專題部分的二輪復習備考中，回歸教材，借助教材中的一些典型例（習）題、探究性欄目等的回顧與探究，經常會有意想不到的收獲.

2 梳理基礎知識，歸納基本方法

在“數列”專題部分的二輪復習備考中，基礎知識是繞不開的一個話題.特別是數列的基本概念，兩個特殊數列的定義、通項與求和公式以及相關的基本性質等，都是數列研究的重要內容，有效構建起一個完整的數列知識體系.

因而，在數列專題的高考二輪復習備考時，要借助對應的數列知識體系，合理滲透相應的數學基本方法，如數列求解中的基本量法，數列通項的整體代換，數列的函數思維，組合與分解的方法，以及數列與不等式的放縮方法等，系統全面地掌握數列的知識以及解決問題的方法.

例2? 〔2024屆浙江省浙南名校聯盟高三（上）第一次聯考數學試卷〕已知數列{an}的首項為a1，且滿足12Sn=4an+1+5n-13，其中Sn為其前n項和，若恒有Sn≤S4（n∈N*），則a1的取值范圍為.

分析：根據數列的遞推關系式來確定數列的通項公式，往往是解決與數列遞推關系式相關問題中最為重要的一個基本步驟.解題的關鍵是利用前n項和Sn與通項an的關系進行變形與轉化，通過關系式的結構特征，借助累加法、累乘法等加以合理變形與應用，是確定數列通項公式中比較常見的技巧方法.

解析：由12Sn=4an+1+5n-13，可得

12Sn+1=4an+2+5n+1-13.

以上兩式對應相減，可得12an+1=4an+2-4an+1+4×5n，即an+2=4an+1-5n，n≥1.

整理，可得an+2+5n+1=4（an+1+5n），即

an+2+5n+1an+1+5n=4，n≥1.

所以a3+52a2+51=a4+53a3+52=……=an+5n-1an-1+5n-2=4，n≥3.

將以上（n-2）個式子累乘，可得an+5n-1a2+51=4n-2，即an+5n-1=4n-2×（a2+5），亦即

an=4n-2×（a2+5）-5n-1，n≥3.

而將n=1代入12Sn=4an+1+5n-13，可得12a1=4a2+5-13，整理有a2=3a1+2，所以an=4n-2×（3a1+7）-5n-1，n≥2.

而對于函數f（x）=4x-2×（3a1+7）-5x-1>0，可得54x-1<3a1+74.由指數函數的單調性，可知存在x0.同理，存在x>t滿足f（x）<0.所以要使得恒有Sn≤S4（n∈N*），只需滿足a4≥0且a5≤0即可.

所以42×（3a1+7）-53≥0，43×（3a1+7）-54≤0，解得1348≤a1≤5964.

故a1的取值范圍為1348，5964.

合理梳理數列中的基礎知識，如涉及數列中前n項和Sn與通項an的遞推關系式問題，可以利用an=S1，n=1，Sn-Sn-1，n≥2，結合an=Sn-Sn-1=f（an）-f（an-1）消去Sn，或利用Sn=f（Sn-Sn-1），消去an求解.而由知識上升為方法，如具體的解題步驟就是升降下標作差，運用通分、合并同類項、因式分解等，借助配湊法、累加（累乘）法、待定系數法等方法，將復雜、不熟悉的數列類型轉化為特殊的等差數列或等比數列類型，在求解過程中往往要對數列的第一項、第二項等加以合理檢驗，避免出現差別與錯誤.

3 掌握基本性質，加強相互聯系

在“數列”專題部分的二輪復習備考中，涉及數列的基本性質及其應用，要加以重點理解與把握，這也是高考命題中最為突出的基本點之一.特別是涉及選擇題與填空題中數列的問題設置，經常離不開數列的基本性質與聯系，因此熟練理解并掌握數列的基本性質也是高考解決好數列問題的關鍵之一.

因而，在數列專題的高考二輪復習備考時，特別要加強不同元素之間的聯系，構建一個完整有機的整體，這樣才方便形成聯系，達到交匯與融合的目的.

例3? （2024屆廣東省佛山市南海區高三摸底考試數學試卷）已知數列{an}對任意k∈N*滿足ak+1+ak=4k+3，則a1+a2 020=（? ）.

A.4 040

B.4 043

C.4 046

D.4 049

分析：根據數列的遞推關系式加以合理數學運算（往往是相加或相減處理），分奇偶項分析，利用等差數列的確定與通項公式的轉化來分析與求解.分奇偶項分別確定數列中相關項的基本性質，進而通過數列的奇偶項特征以及對應的特殊數列類型加以分析與解決問題.

解析：由ak+1+ak=4k+3，可得

ak+2+ak+1=4（k+1）+3=4k+7.

以上兩式相減，可得ak+2-ak=4，所以數列{a2k}，{a2k-1}均是以4為公差的等差數列，則有a2k=a2+4（k-1）.

而a2+a1=4×1+3=7，則有a2k=a2+4（k-1）=7-a1+4（k-1）=4k+3-a1，所以a1+a2 020=4×1 010+3=4 043.

數列的基本性質的歸納與應用，往往是解決問題的關鍵所在.如解決以上涉及數列中的奇偶項綜合問題，往往是抓住題設條件中數列的遞推關系式的結構特征，通過多寫幾項的形式，從中合理觀察，巧妙歸納，進而挖掘相應的性質與規律，為選擇合適的技巧與方法提供思維方向.

在高考二輪復習備考中，整個復習備考過程也是一個知識積累與經驗積累的過程.在這個積累過程中，不斷強化與交匯，形成更高層次的解題習慣與方法，進而從中合理提煉出基本的數學思想方法.

基于此，在數列專題的高考二輪復習備考時，重視教材，梳理知識，掌握性質，積累經驗等成為一個很好嘗試，有效打好基礎，優化歸納方法，巧妙加強聯系，系統提煉思想，促進復習備考的提優增速.

今后幾年高考數學“數列”專題試題著力創新情境的設置，優化難度的調控，更加突出新課程改革的要求與新高考的“指揮棒”，契合考試的人才選拔與高中的育人價值功能，充分體現“平和之中有乾坤，變化之處見功力”.