基于深度學習的“函數的單調性”概念教學

左婷

課題信息：江蘇省教育科學“十四五”規劃2022年度課題“指向深度學習的高中數學單元教學策略研究”，立項編號為C/2022/02/05.

1 深度學習的基本思維

1.1 概念內涵的深層理解

基于數學概念課堂的教學實踐與深度學習，從概念層面挖掘，剖析概念的內涵與實質，以及相關概念的來龍去脈與關聯，從而聯系相關概念的外延與應用，全面構建數學知識體系，形成不同概念之間的節點與聯系，促進不同數學知識之間的轉化與應用.

1.2 數學思維的深層應用

基于數學概念課堂的教學實踐與深度學習，由知識到思維逐步深入，借助構造、類比、聯系、創新等思維方式，展示知識所對應的思維，加深對知識的理解與掌握，從思維層面形成數學習慣，構建更加良好的思維品質與核心素養.

1.3 創新應用的深層拓展

基于深度學習，有效構建數學知識、數學思想、數學經驗等方面之間的融合，形成更加完善與系統的知識網絡體系與架構，對于數學應用與創新應用等都有較好的提升與拓展作用.

2 深度學習的教學過程

2.1 導學聚焦

基于深度學習的“函數的單調性”概念教學的導學聚焦如表1.

表1

教材考點

學習目標

核心素養

函數單調性的概念、判定與證明

了解函數單調性（增函數、減函數）的概念，會用定義判斷或證明函數的單調性

直觀想象、邏輯推理

求解函數的單調區間

會借助函數的圖象或函數單調性的定義確定或求解函數的單調區間

數學運算、直觀想象

函數單調性的簡單應用

會根據函數的單調性求解相關參數值或求解參數不等式問題等

數學運算、邏輯推理、直觀想象

2.2 問題導學

預習教材（人教A版數學必修第一冊）第三章第二節“函數的基本性質”，對應教材的位置是第76～79頁，并思考下列相關問題：

（1）如何定義單調遞增與單調遞減？增函數、減函數的概念又是怎樣的？

（2）函數的單調性與函數圖象變化規律有何關系？函數的單調性和其對應的單調區間有何關系？

2.3 情境引入

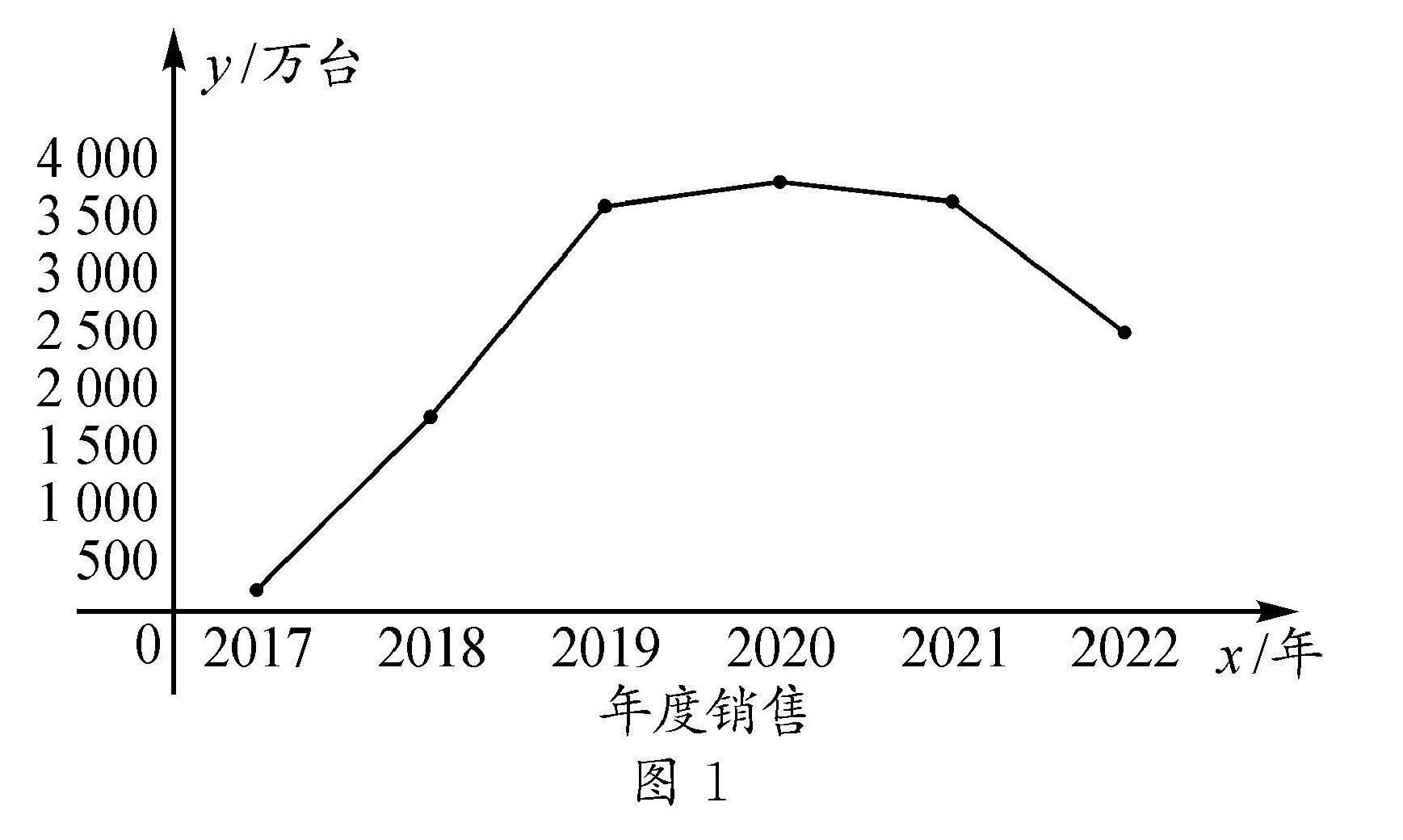
材料1：目前，國內市場銷量前三的智能音響分別是：第三名，天貓精靈（浙江）；第二名，小愛同學（北京）；第一名，小度（北京）.圖1是2017—2022年中國智能音響市場銷售量變化圖.

問題1? （1）上述情境中變量分別是什么，哪一個變量隨著另一個變量的變化而變化？

（2）從左到右，圖象的變化規律是什么？

材料2：二十四節氣，是中華民族悠久歷史文化的重要組成部分.我們的祖先通過它能直觀地了解一年中季節氣候的變化規律，它在安排和指導農業生產中，發揮了重大作用.圖2是某地一年的氣溫變化圖.

問題2? 氣溫隨著時間的改變如何變化，圖象的變化規律是什么？

2.4 新知探究

（1）增函數、減函數的概念

一般地，設函數f（x）的定義域為I，區間DI：

①如果x1，x2∈D，當x1＜x2時，都有f（x1）＜f（x2），那么就稱函數f（x）在區間D上單調遞增（如圖3）.

②如果x1，x2∈D，當x1＜x2時，都有f（x1）＞f（x2），那么就稱函數f（x）在區間D上單調遞減（如圖4）.

特別地，

當函數f（x）在它的定義域上單調遞增（減）時，我們就稱它是增（減）函數.

【微思考1】①在函數單調性的定義中，能否去掉“任意”？

（提示：不能.不能用特殊代替一般）

②x1，x2∈D，若（x2-x1）［f（x2）-f（x1）］＞0，則y=f（x）在某個區間D上單調遞增嗎？若（x2-x1）［f（x2）-f（x1）］＜0，則y=f（x）在某個區間D上單調遞減嗎？簡要說明原因.

（提示：是.若（x2-x1）［f（x2）-f（x1）］＞0則x2-x1與f（x2）-f（x1）同號，即x2＞x1時，f（x2）＞f（x1），所以f（x）在D上單調遞增；

同理（x2-x1）［f（x2）-f（x1）］＜0時，f（x）在D上單調遞減.）

③x1，x2∈D，若f（x2）-f（x1）x2-x1＞0，則y=f（x）在區間D上單調遞增嗎？若f（x2）-f（x1）x2-x1＜0，則y=f（x）在區間D上單調遞減并簡要說明原因.（

提示：是.若f（x2）-f（x1）x2-x1＞0，則x2-x1與f（x2）-f（x1）同號，即x2＞x1時，f（x2）＞f（x1），所以f（x）在D上單調遞增；

同理f（x2）-f（x1）x2-x1＜0時，f（x）在D上單調遞減.）

（2）函數的單調性與單調區間

如果函數y=f（x）在區間D上單調遞增或單調遞減，那么就說函數y=f（x）在這一區間具有（嚴格的）單調性，區間D叫做y=f（x）的單調區間.

【微思考2】區間D一定是對應函數的定義域嗎？（

提示：不一定，可能是定義域的一個子區間，單調性是局部概念，不是整體概念.）

2.5 新知應用

（1）函數單調性的判定與證明

例1? 根據定義，研究函數f（x）=axx—1（a≠0）在x∈（-1，1）上的單調性.（a＞0時，單調遞減;a＜0時，單調遞增.）

點評：利用函數的單調性的定義判斷和證明函數單調性的基本步驟如圖5所示.

這里要注意：作差變形是判斷和證明函數單調性的關鍵所在，且變形的結果多為幾個因式乘積的形式.

（2）函數單調區間的確定與求解

例2? 畫出函數y=|-x2+2x+3|的圖象，并指出函數的單調區間.（增區間為［-1，1］，［3，+∞）；減區間為（-∞，-1］，（1，3）.）

點評：確定與求解函數的單調區間的兩種常見方法如圖6所示.

3 深度學習的教學啟示

基于數學概念課堂的教學實踐與深度學習，立足數學基礎知識，特別是數學概念與性質所對應的內涵，從而從概念或性質等視角切入，進行多視角的深度學習，對于基礎性的把握更加到位.

借助深度學習，將相應的數學概念進行“串點成線、織網鋪面”，構建一個完善的數學知識體系，從而有效夯實學生的“四基”，培養學生的“四能”，強化創新意識與創新應用，培育理性思維，促進學生高階思維、核心素養的發展.