回歸概念探本質，經歷實演提素養

童元意

摘要：本文中從引導學生觀察、動手操作體驗入手，緊扣概念設計層層遞推的問題鏈，在舉例說明過程中加深對概念的理解，在參與合作交流、辯析問題中探尋概念的本質，培養學生的直觀想象能力和邏輯推理能力，提升數學素養.

關鍵詞：回歸概念;動手實踐;概念本質

1 問題的提出

數學概念是數學學習的基石，是基礎知識和基本技能教學的核心，是數學的邏輯起點，正確理解概念是學好數學最重要的一環.數學素養差異關鍵是在對數學概念的理解、方法的運用和轉化等方面的差異.《普通高中數學課程標準（2017年版2020年修訂）》指出：“有效的數學學習過程不能單純地依賴模仿與記憶，教師應當引導學生主動地從事觀察、實驗、猜測、驗證、推理、操作與交流等數學活動.”因此，回歸概念、經歷實演對提升數學素養顯得尤為重要，本文中嘗試以

（2019人教A版必修第二冊第八章第6節）

“空間直線、平面的垂直”為例進行說明.

2 回歸概念、參與探求概念本質的一些途徑

（1）觀察、直觀感知，讓學生經歷從現實生活中發現問題的過程

案例? “空間直線、平面的垂直”設計

環節1：創設生活情境，發現問題.

問題1? 生活中常見線與面相交.詩人王維有千古絕句“大漠孤煙直，長河落日圓”.

①如圖1，你認為這縷孤煙與大漠地平面，以及旗桿與地面給人什么形象？

②說出旗桿與地面、大橋橋柱與水面是什么位置關系？你能舉出一些類似的例子嗎？

問題2? 利用幾何畫板演示太陽在動，影子也跟著動的動態畫面.

①如圖2，在陽光下觀察直立于地面的旗桿AB及它在地面的影子BC，旗桿所在的直線與影子所在直線位置關系是怎樣的［1］？

②如圖3，旗桿AB與地面上任意一條不過旗桿底部B的直線B′C′的位置關系又是怎樣的？

追問：通過觀察，怎樣判定直線與平面垂直？

設計意圖：以直觀感性的材料作支撐，引導學生觀察，體會空間圖形在生活中處處可見，教學中不過早地給出結論，讓學生從已有的認知上初步建構直線與平面垂直的模型概念，為后面的概念學習做好鋪墊.

（2）動手實驗，操作確認，讓學生經歷從具體到抽象的過程

環節2：動手實踐演示，提出問題.

問題3? 如圖4，拿出準備好的（任意）三角形紙片，過△ABC的頂點A翻折紙片，得到折痕AD，將翻折后的紙片豎直放置在桌面上，如圖5，折痕與桌面垂直嗎？（演示不同位置的折痕紙片放置在桌面上.）隨著折痕位置的移動，你有什么發現？

問題4? 如何翻折才能使折痕AD與桌面所在的

平面垂直？由折前AD⊥BC，翻折之后，AD⊥CD，AD⊥BD會發生變化嗎？由此你能得到什么結論？

設計意圖：歐拉曾說過，數學這門科學，需要觀察，還需試驗.在折紙試驗中，會出現“垂直”與“不垂直”兩種情況，引導學生交流，回歸概念，分析原因.隨著折痕AD位置的移動，探求直線與平面垂直的條件.動畫展示試驗成果，增強學生興趣，培養學生“用數學”的意識，促使學生的空間想象模型化.

（3）多辨析，多舉例，暴露思維誤區，經歷從模糊到逐漸清晰的過程

環節3：辨析舉例中，理解概念.

教學中要讓學生自己進行概念的建構，否則對概念的理解只能停留在表面的字眼上.如讓學生舉例和講解，從似是而非的概念中甄別，加深對概念的理解，豐富概念結構的內涵.過程中要尊重學生已有的水平，接受學生看待問題的方式，容忍學生的錯誤.

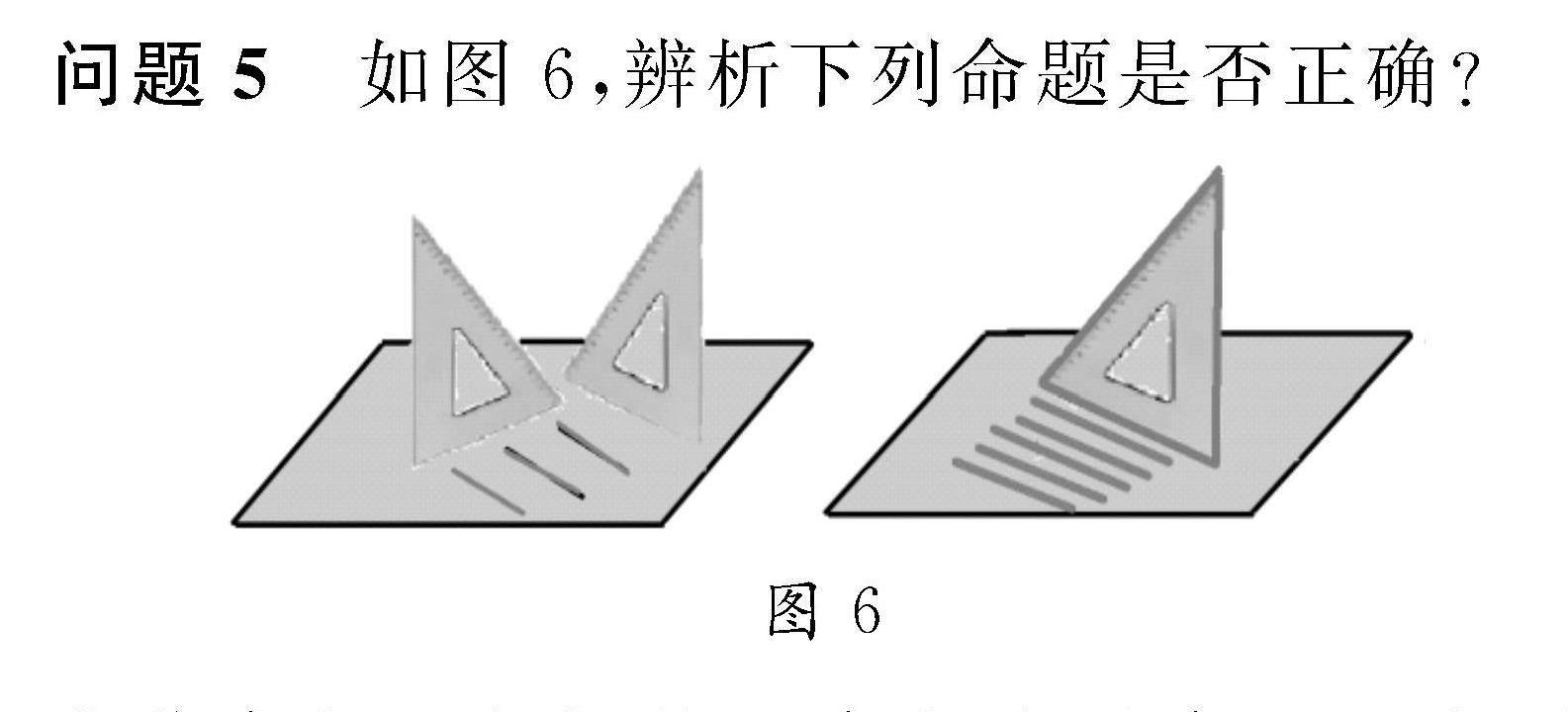
問題5? 如圖6，辨析下列命題是否正確？

①若直角三角板的一直角邊垂直于一個平面內的無數條直線，那么這條直角邊所在的直線與這個平面垂直.

②若一條直線與一個梯形的兩條邊垂直，那么這條直線垂直于梯形所在的平面.

③如果一直線不垂直于一個平面，那這條直線不垂直于此平面內的任意一條直線.

問題6? 如圖7，在教室這個長方體模型中，你能找到哪些直線與地面垂直？哪些直線與黑板所在的平面垂直？

設計意圖：給出了概念，并不代表學生理解了概念.舉例既是對學生原有知識結構的一次沖擊和洗禮，也為學生建構新知識體系搭建了橋梁和平臺.

（4）問題鏈設計，讓知識理解更深刻，經歷從理解概念到掌握概念的過程

數學概念是思維的基礎，也是思維的結果.恰當地展示其形成過程，拉長被壓縮了的“知識鏈”，恰當恰時的問題鏈是對數學抽象與數學模型方法進行點悟的極好素材和契機.

環節4：問題鏈練習中，鞏固概念.

問題7? 在立方體ABCD-A′B′C′D′中，

①直線BD與平面AA′C′C是否垂直？

②直線A′C與平面BDC′是否垂直？

③與平面A′BCD′垂直的棱有哪幾條？

設計意圖：以熟悉的重要模型立方體為背景材料，設計問題鏈，層層遞進，引導學生從不同角度思考，加深對概念的理解和掌握.教師要“沉入教材”細細“揣摩”，發掘問題的內在聯系，“頓悟”概念的內涵.

（5）重視回顧檢測，完善概念結構

環節5：歸納小結，目標檢測，課堂深度拓展.

問題8? ①判定直線與平面垂直的主要思路是什么？②按照怎樣的路徑展開直線與平面垂直的探究？③判定定理中所蘊含的數學思想方法是什么？

問題9? 如圖8，長方體AC1中，

①棱與面對角線中，有哪些直線與平面垂直？

②當底面矩形ABCD滿足什么條件時，直線BD⊥平面AA1C1C？

③過點C1如何作直線l⊥平面A1B1CD？

設計意圖：考查學生對直線與平面垂直判定定理的理解和應用.愛因斯坦曾說，提出一個問題往往比解決一個問題更重要，因為解決一個問題僅僅是技能而已，而提出新的問題，從新的角度去看舊的問題，卻需要有創造性的想象力，標志著科學的真正進步.

3 教學反思

（1）教師要理解學生，了解學生原有知識結構，遵循學生思維發展的合理性.本節課內容相對較少，但蘊含著非常豐富的方法和思想，空間垂直概念相對直線與平面平行要難，要留足時間讓學生獨立思考和探索.不要急于給出答案，對于學生的獨創方法不要全盤否定，要善于發現其中有價值的閃光點.

（2）線線、線面、面面等位置關系是立體幾何考查的核心［2］，特別是平行與垂直關系，突出立體幾何中“觀察、判斷、計算、證明”的解決問題的途徑.本節課通過觀察—實驗—猜測—驗證—辨析概念—問題鏈—目標檢測等環節，一步步展開探究，教學生學會研究一個幾何對象的基本思路，為后續學習直線與平面垂直的性質定理及平面與平面垂直積累數學活動經驗.

（3）空間圖形的學習要引導學生借助于長方體（正方體）這一熟悉的模型，學會“聯想”，通過直觀感知、操作確認、推理論證、度量計算等能夠較好地認識和理解空間中的點、直線與平面間的位置關系和度量關系，深度挖掘空間點、直線、平面之間的位置關系進而提出問題，可加深學生的體驗，加深對概念的理解和鞏固.立體幾何教學中要引導學生從有圖想圖到無圖想圖，形成解決立體幾何問題的基本思維模式，這樣可以有效提升直觀想象、邏輯推理和數學運算等核心素養.

參考文獻：

［1］中華人民共和國教育部.普通高中數學課程標準（2017年版2020年修訂）［S］.北京：人民教育出版社，2020.

［2］姚強.基于發展學生數學核心素養目標的問題設計——以“直線的點斜式方程”教學為例［J］.

中學數學教學參考，2022（19）：22-24.