借助“直觀”啟發(fā)幾何問題解決

趙文倩

[ 摘 要 ]文章以三角形中位線定理的再證明為抓手，梳理利用“幾何直觀”培養(yǎng)學(xué)生分析、探究能力的圖形表象、實(shí)驗(yàn)、知識(shí)聯(lián)想、數(shù)形結(jié)合等方法，揭示借助“幾何直觀”發(fā)現(xiàn)解決問題方法的基本套路，并應(yīng)用套路解決新問題，以培養(yǎng)學(xué)生的分析探究能力.

[ 關(guān)鍵詞 ]核心素養(yǎng)；幾何直觀；中位線定理

“幾何直觀”的內(nèi)容和要求

“幾何作為一種理解、描述和聯(lián)系現(xiàn)實(shí)空間的工具，也許是數(shù)學(xué)中最直觀、具體和真實(shí)的部分”[1]（Mam？ mana&Villani，1998），所以《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022年版）》（下文簡稱《標(biāo)準(zhǔn)》）把幾何直觀作為核心素養(yǎng)的主要表現(xiàn)之一.《標(biāo)準(zhǔn)》指出：幾何直觀要求能夠感知各種幾何圖形及其組成元素，依據(jù)圖形的特征進(jìn)行分類，幾何直觀有助于把握問題的本質(zhì)，明晰思維的路徑.

幾何直觀是思考問題、解決問題的重要思維方式之一，是直接“從感覺的具體的對象背后，發(fā)現(xiàn)抽象的、理想的（狀態(tài)）的能力”.對幾何直觀最貼切的表述應(yīng)該是史寧中教授的：思路是看出來的，不是證出來的[2].這里的“看出”，就是憑借幾何直觀洞悉幾何元素的內(nèi)在聯(lián)系，這不僅有助于探索問題解決的思路，而且可以獲得對數(shù)學(xué)的直觀理解，抓住問題的本質(zhì).

借助“幾何直觀”解決幾何問題的實(shí)踐

根據(jù)直觀性的表現(xiàn)，我們是否可以在幾何問題中借助直觀來認(rèn)識(shí)和理解問題，同時(shí)幫助人們探索問題、促進(jìn)發(fā)現(xiàn)呢？如三角形中位線定理，傳統(tǒng)課堂在提出“你能根據(jù)猜想進(jìn)行證明嗎？”這一問題后，學(xué)生直接回答自己的證明方法，然后進(jìn)入應(yīng)用環(huán)節(jié).這種做法，對學(xué)生而言，并沒有經(jīng)歷定理的探究過程，只是接受了一種數(shù)學(xué)事實(shí).實(shí)踐證明，學(xué)生很多時(shí)候遇到幾何問題解決不了，是卡在第一步，即無從下手，不知道朝什么方向思考，簡單地說，就是不知道如何添加輔助線.這就需要學(xué)生利用“幾何直觀”分析和探究問題，找到圖形間的內(nèi)在聯(lián)系以及解決問題的方向，從而達(dá)到問題解決的目的.

為了幫助學(xué)生明確對幾何圖形的直觀感受，并且運(yùn)用這種直觀感受，筆者將九年級總復(fù)習(xí)階段的學(xué)生作為教學(xué)對象，以中位線的性質(zhì)證明的再探究、再經(jīng)歷、再創(chuàng)造、再應(yīng)用為例，通過如下環(huán)節(jié)予以說明.

環(huán)節(jié)一 利用紙片折痕，感受直觀內(nèi)涵.

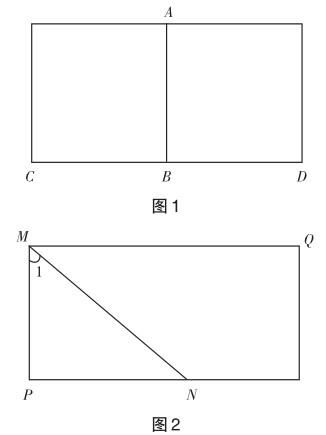
提問 請猜想圖1中線段AB與線段CD之間的位置關(guān)系，并猜想圖2中∠1的度數(shù).

設(shè)計(jì)意圖 將圖1所示的矩形沿著AB對折，發(fā)現(xiàn)折疊后的BD與

BC完全重合，所以AB與CD垂直.將圖2所示的矩形沿著MN折疊，發(fā)現(xiàn)邊MP與MQ不重合，驗(yàn)證了猜想∠1=45°是不準(zhǔn)確的.引導(dǎo)學(xué)生認(rèn)識(shí)到一些結(jié)論正確與否可通過觀察猜想、操作認(rèn)證這種“直觀”的方法予以驗(yàn)證，從而建立直觀觀念.

環(huán)節(jié)二 再探中位線，打開直觀空間.

提問 上述證法一、二，你是從什么角度想到可以這樣解決問題的？

回答 ①看圖形很像相似中的“A”型相似，于是嘗試用相似來解決；②要證明平行，可以利用三線八角，從而想到利用相似證明角相等；③由“平行且相等”聯(lián)想到構(gòu)造平行四邊形，只要證明四邊形DBCO是平行四邊形就可以得到結(jié)論.

教學(xué)意圖 “是這樣”“會(huì)這樣”等直觀意識(shí)是解決問題的起點(diǎn)，“A”型相似簡單、易懂，能讓學(xué)生感受到直觀的魅力、知識(shí)的力量；而由“平行且相等”聯(lián)想到平行四邊形，回顧了已學(xué)知識(shí)，帶動(dòng)了再探究的發(fā)生.

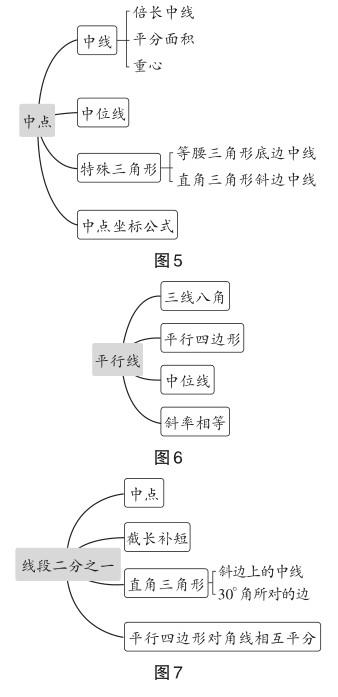
2.系統(tǒng)梳理，拓寬直觀

提問 拋開中位線定理的證明，看到“中點(diǎn)”“平行”“線段倍分”這些關(guān)鍵詞，你會(huì)想到哪些相關(guān)的知識(shí)和方法？

學(xué)生表達(dá)，教師板書，形成如下思維導(dǎo)圖（如圖5、圖6和圖7）.

提問 你發(fā)現(xiàn)更多的證明方法了嗎？

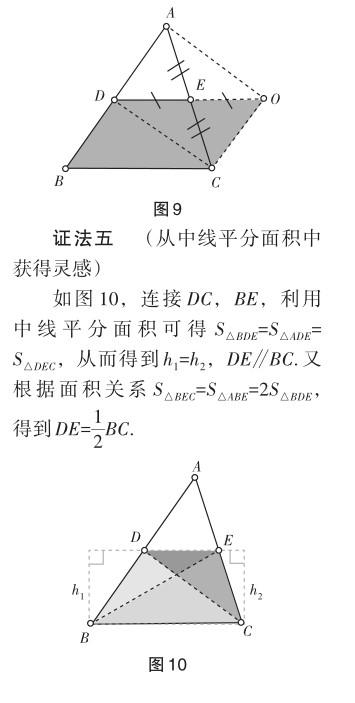
證法三 （從倍長中線方法中獲得靈感）

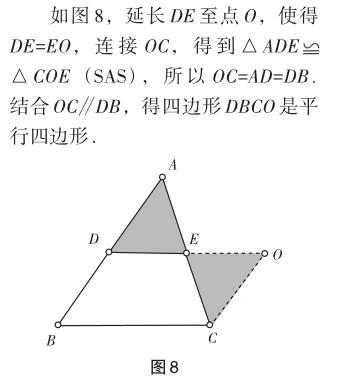
證法四 （從對角線互相平分中獲得靈感）

如圖9，延長DE至點(diǎn)O，使得DE=EO，連接OC，DC，AO.由于對角線互相平分，證得四邊形ADCO是平行四邊形.再根據(jù)CO∥AD∥BD，CO=AD=BD，得到四邊形BDOC是平行四邊形.

證法六 （從中點(diǎn)坐標(biāo)公式中獲得利用解析法解決問題的靈感）

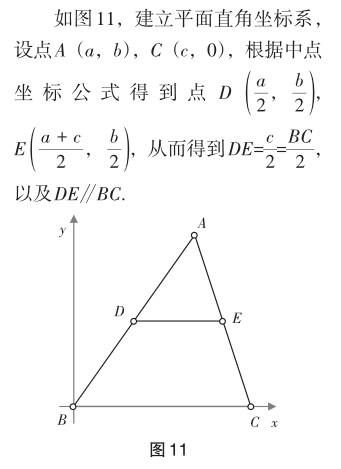
證法豐富，此處不一一羅列.

教學(xué)意圖 從直觀到猜想、驗(yàn)證、證明，是幾何學(xué)習(xí)的基本套路.學(xué)生圍繞已知證法中包含的關(guān)鍵詞的知識(shí)梳理，拓展了思路，形成了更豐富的直觀觀念，其中解析法的直觀、簡明，讓學(xué)生獲得了更愉快的學(xué)習(xí)體驗(yàn)，為之后問題的解決提供了更豐富的直觀路徑.

環(huán)節(jié)三 借助直觀思維，解決真實(shí)問題.

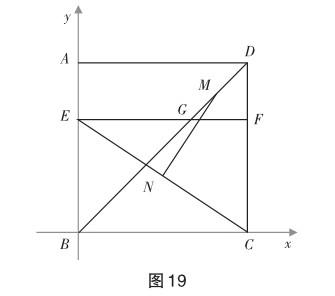
問題 如圖12，四邊形ABCD是邊長為8的正方形，點(diǎn)E在邊AB上，BE=6，過點(diǎn)E作EF∥BC，分別交BD，CD于G，F(xiàn)兩點(diǎn).若M，N分別是DG，CE的中點(diǎn)，求MN的長.

（課堂上，學(xué)生展示其看到的、想到的、直觀分割的，猜測、驗(yàn)證并證明）

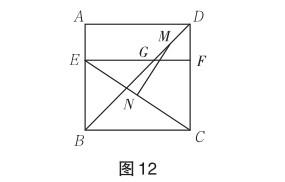
解法一 （利用“圖形表象”中的“正方形垂直特性”獲得圖形直觀）

如圖13，利用垂直分割，過點(diǎn) M，N分別作BC，DC的垂線，構(gòu)成三邊長分別為3，4，5的直角三角形MNO.

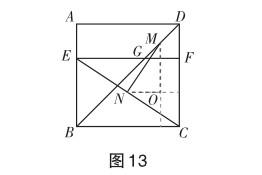
解法二 （利用“知識(shí)聯(lián)想”中的“中位線”獲得思路直觀）

如圖14、15，學(xué)生觀察發(fā)現(xiàn)題目中出現(xiàn)兩個(gè)中點(diǎn)，但是兩個(gè)中點(diǎn)沒有出現(xiàn)在同一個(gè)三角形中，故而想到利用矩形的對角線構(gòu)造中點(diǎn)，形成新的中位線解決問題.圖14中的MO，NO分別是△GCD和△EGC的中位線，圖15中的MO，NO分別是△EGD和△ECD的中位線，它們均構(gòu)成三邊長分別為3，4，5的直角三角形MNO.

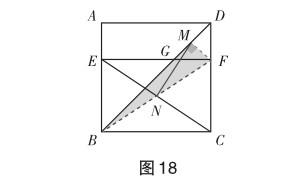
解法五 （利用“擬實(shí)驗(yàn)”中的“測量”，結(jié)合“知識(shí)聯(lián)想”中的“中線”獲得直觀）

解法四中學(xué)生測量后發(fā)現(xiàn)MN的長度大致是5，有些學(xué)生直觀聯(lián)想到矩形的對角線相等，那么MN除了是EC長度的一半，是否也是FB長度的一半呢？如圖18，連接MF后，只要證明△MBF是直角三角形即可.朝著觀察猜想的方向努力，自然發(fā)現(xiàn)MF是等腰直角三角形DGF的中線，易得△MBF是直角三角形，從而得解.

解法六 （利用“數(shù)形結(jié)合”獲得代數(shù)直觀）

如圖19，建立平面直角坐標(biāo)系，首先可以得到點(diǎn)E，C的坐標(biāo)，又因?yàn)镈B是正方形的對角線，于是易得點(diǎn)D，G的坐標(biāo)，利用中點(diǎn)坐標(biāo)公式可得點(diǎn)M，N的坐標(biāo).最后利用兩點(diǎn)間的距離公式或構(gòu)造直角三角形都可以很快得解.

教學(xué)意圖 應(yīng)用是檢驗(yàn)教學(xué)成敗的有效手段，通過直觀建立起的觀念能不能在問題解決中發(fā)揮作用，是衡量本節(jié)復(fù)習(xí)教學(xué)有效性的一個(gè)重要因素.本環(huán)節(jié)與前期探究緊密結(jié)合，學(xué)生分享所悟、所猜、所證，如解法一的垂直分割、解法四通過測量猜想△EMC是等腰直角三角形、解法六的以數(shù)定形的數(shù)形結(jié)合等，都體現(xiàn)了利用各類方法獲得幾何直觀后處理問題的有效性，利用解法的多樣性使得幾何問題成為思維訓(xùn)練的良好素材.

學(xué)生通過“垂直分割試一試”“我感到它是……”“我量一量發(fā)現(xiàn)……”等直觀的學(xué)習(xí)方式找到了問題解決策略，實(shí)現(xiàn)了直觀路徑多元，解答策略多樣.

利用“幾何直觀”培養(yǎng)分析、探究能力的方法

（一）以已有知識(shí)作為“幾何直觀”的培養(yǎng)起點(diǎn)

在初中幾何學(xué)習(xí)中，學(xué)生往往先利用經(jīng)驗(yàn)、直覺去推理，就像本課例中，有的學(xué)生利用中點(diǎn)倍長中線、構(gòu)造中位線，有的學(xué)生利用中線構(gòu)造直角三角形，這些都是建立在學(xué)生已有的數(shù)學(xué)經(jīng)驗(yàn)之上的.接著，在教師所設(shè)計(jì)的問題引導(dǎo)下，學(xué)生探究新的數(shù)學(xué)策略，解決新的問題，形成宏觀認(rèn)識(shí).從學(xué)習(xí)心理上來看，這樣的教學(xué)設(shè)計(jì)對學(xué)生建立數(shù)學(xué)學(xué)習(xí)的認(rèn)識(shí)，并化解不必要的心理障礙是有利且有效的.

本節(jié)課中，我們嘗試?yán)弥形痪€定理的證明，將“碎片化教學(xué)”整合起來，通過學(xué)生獨(dú)立思考、交流方法逐步感悟數(shù)學(xué)思想方法.不要僅僅成為做題的機(jī)器，不要迷戀解題上的一招一式，要注重過程中的通性通法.當(dāng)學(xué)生獨(dú)立面對一個(gè)數(shù)學(xué)對象時(shí)，要學(xué)會(huì)如何研究一個(gè)數(shù)學(xué)對象，明白研究內(nèi)容、思路和方法是什么，初中幾何教學(xué)要注重學(xué)生幾何直觀的發(fā)展.

（二）獲得“幾何直觀”的策略

1.利用“圖形表象”獲得圖形直觀

根據(jù)學(xué)生對圖形的認(rèn)知可以將幾何概念劃分為以下三個(gè)層次：最低層次是直觀概念，這一層次一般只涉及圖形的形狀，而與圖形元素的性質(zhì)和關(guān)系無關(guān)；第二層次屬于分析層次，不僅需要觀察圖形的直觀，更要對圖形的位置與度量特征等進(jìn)行分析；第三層次是一些由公理系統(tǒng)所“生成”的，也就是由幾何推理得到二級結(jié)論[2].

學(xué)生處理幾何問題多停留在最低層次，而初中階段的綜合性幾何問題，要求學(xué)生達(dá)到更高層次，所以在對圖形進(jìn)行觀察后，教師應(yīng)及時(shí)引導(dǎo)學(xué)生對圖形中的條件進(jìn)行組合，得到一些基本圖形.視覺是一種直覺（有時(shí)對發(fā)現(xiàn)證明是必需的）的工具.例如環(huán)節(jié)三中存在矩形AEFD、矩形EBCF、等腰直角三角形EBG、等腰直角三角形DFG、等腰直角三角形ABD等，這些基本圖形的得出可以幫助我們在解題時(shí)得到一些有益的結(jié)論，例如：連接MF，則MF與DG垂直；連接BF，則BF=EC，N為BF的中點(diǎn)等.

2.利用“擬實(shí)驗(yàn)”獲得結(jié)論直觀

幾何量都可以用距離、角度等來進(jìn)行刻畫，因此，學(xué)生可以通過各種測量工具進(jìn)行實(shí)驗(yàn).雖然這樣的“實(shí)驗(yàn)”不具有科學(xué)性，因?yàn)樵倬艿臏y量儀器都會(huì)產(chǎn)生誤差，卻有助于學(xué)生去接受從而演繹得到概念，這種方式被稱為“擬實(shí)驗(yàn)”[1].

學(xué)生可以通過“擬實(shí)驗(yàn)”獲得可能的結(jié)論，進(jìn)階的圖形直觀來自“操作”.課堂上從矩形紙片中的線和角入手，學(xué)生利用折疊、測量等方式進(jìn)行簡單驗(yàn)證，通過“擬實(shí)驗(yàn)”獲得可能的結(jié)論就是幾何直觀的一種.不是所有的“擬實(shí)驗(yàn)”都是正確的，但可以為我們解決問題提供方向.在環(huán)節(jié)三中的解法四、五中，學(xué)生動(dòng)手測量后發(fā)現(xiàn)MN的長度大致是5，于是猜想其是EC長度的一半，則出現(xiàn)解法五猜想MN的長度是FB長度的一半，以及解法四關(guān)注題目中要素之間的聯(lián)系.

3.利用“知識(shí)聯(lián)想”獲得思路直觀

數(shù)學(xué)猜想是數(shù)學(xué)學(xué)習(xí)過程中的一種重要方法，許多重要的數(shù)學(xué)理論都來自數(shù)學(xué)猜想.然而猜想不是空想，是學(xué)生在教師創(chuàng)設(shè)的情境下有方向地推測和判斷，是基于學(xué)生已有知識(shí)做出的合理猜測.例如通過“聯(lián)想相關(guān)知識(shí)點(diǎn)”使條件和結(jié)論之間建立聯(lián)系，從而形成有效的數(shù)學(xué)猜想，可以幫助學(xué)生更快地找到問題的突破口，從而增強(qiáng)學(xué)生的學(xué)習(xí)信心.

環(huán)節(jié)二中，學(xué)生分享的方法有限，當(dāng)多解問題分享停滯時(shí)，就是分享用“知識(shí)聯(lián)想”獲得直觀，從而解決問題的最佳時(shí)機(jī).教師適時(shí)介入，指導(dǎo)學(xué)生發(fā)散思維，利用“知識(shí)聯(lián)想”打開思路，引導(dǎo)學(xué)生將學(xué)習(xí)的方式從“已知輔助線后進(jìn)行證明和學(xué)習(xí)用多種方法證明”，轉(zhuǎn)變?yōu)椤霸趺磿?huì)想到這樣解決問題，怎么想到這樣添加輔助線”；引導(dǎo)學(xué)生嘗試?yán)妙}目和結(jié)論中的一些關(guān)鍵詞來展開想象，從中選取合適的方法解決問題.在環(huán)節(jié)三的解法二、三中，學(xué)生根據(jù)中點(diǎn)發(fā)散思維，思考涉及的方法，使這種“聯(lián)想型直觀”得以落實(shí).

4.利用“數(shù)形結(jié)合”獲得代數(shù)直觀

眾所周知，解析幾何的誕生是近代數(shù)學(xué)的第一個(gè)里程碑.解析幾何是“數(shù)形結(jié)合”的重要應(yīng)用，是以平面直角坐標(biāo)系為研究工具，通過代數(shù)運(yùn)算研究幾何圖形，這是幾何直觀方法中重要的一種.在實(shí)際教學(xué)中，有的教師將這種“數(shù)形結(jié)合”簡單化為“平面直角坐標(biāo)系中的計(jì)算”教學(xué)以及套用公式，這背離了“數(shù)形結(jié)合”思想.平面幾何教學(xué)中的一個(gè)明顯感受是很難得出某些幾何元素之間的關(guān)系，但在解析幾何中借助平面直角坐標(biāo)系，我們可以通過坐標(biāo)和代數(shù)語言來準(zhǔn)確描述這些關(guān)系[3].

環(huán)節(jié)三的解法六，利用平面直角坐標(biāo)系解決幾何問題，這是最有“幾何直觀”味道的方法，也就是利用代數(shù)來刻畫幾何規(guī)律.在利用“代數(shù)刻畫”獲得直觀時(shí)需要注意以下兩點(diǎn)：一是要注意學(xué)生是否具備解析的基礎(chǔ).例如，必須能夠熟練運(yùn)用中點(diǎn)坐標(biāo)公式和兩點(diǎn)間距離公式等.二是方法分享后及時(shí)引導(dǎo)學(xué)生思考看到哪些要素可以想到用解析法解決問題.例如，看到平行四邊形、特殊平行四邊形（菱形的對角線為坐標(biāo)軸、矩形、正方形）、平行線等，不應(yīng)僅停留在解決問題上，更要關(guān)注是怎么想到的.

（三）“幾何直觀”培養(yǎng)過程中的情感、態(tài)度與價(jià)值觀

在分享數(shù)種解法的過程中，我們驚喜地發(fā)現(xiàn)，學(xué)生很好地利用了幾何中的直觀，著重分享了知識(shí)的發(fā)生過程，而不僅僅是證明過程.在學(xué)生談體會(huì)中筆者發(fā)現(xiàn)，不少學(xué)生轉(zhuǎn)變了學(xué)習(xí)數(shù)學(xué)的角度，從被動(dòng)學(xué)習(xí)轉(zhuǎn)化為主動(dòng)學(xué)習(xí)，能夠積極地想到，并進(jìn)一步去做到.

英國教育家懷特海曾經(jīng)說過：“教育是教人們?nèi)绾芜\(yùn)用知識(shí)的藝術(shù).當(dāng)你丟掉你的課本，燒掉你的聽課筆記，忘掉了你為了應(yīng)付考試而背誦的細(xì)節(jié)，你的學(xué)習(xí)對你來說才是有用的.”顯然，那些“丟掉的、燒掉的、忘掉的”應(yīng)該就是單純的知識(shí)，“剩下的”應(yīng)該就是學(xué)生在獲得這些知識(shí)的過程中所用到的解決問題的方法、思想、素養(yǎng)[4].研究問題的方法、看待問題的角度、數(shù)學(xué)的思維、克服困難的精神才是真正的數(shù)學(xué)核心素養(yǎng)，才是一節(jié)課中需要突破的關(guān)鍵環(huán)節(jié).

參考文獻(xiàn)：

[1]鮑建生，周超.數(shù)學(xué)學(xué)習(xí)的心理基礎(chǔ)與過程[M].上海：上海教育出版社，2009.

[2]史寧中.數(shù)學(xué)課程標(biāo)準(zhǔn)修訂與核心素養(yǎng)[J].教育研究與評論，2022（05）：18-27.

[3]章建躍.利用幾何圖形建立直觀 通過代數(shù)運(yùn)算刻畫規(guī)律——解析幾何內(nèi)容分析與教學(xué)思考（之一）[J].數(shù)學(xué)通報(bào)，2021，60（07）：7-14.

[4]岳紹杰，于彬.一次市級初中數(shù)學(xué)優(yōu)質(zhì)課評選的亮點(diǎn)展示與評析[J].中學(xué)數(shù)學(xué)月刊，2020（05）：28-30.