立足基本圖形 提升解題能力

姚正江

[ 摘 要 ]基本圖形是解決圖形問題的基礎，“兩相等線段共用一端點”這一基本圖形在初中數學幾何解題中具有重要地位.文章以該基本圖形的專題復習教學為例，分別從“開門見山，揭露主題”“借助圖形，夯實基礎”“應用圖形，深化理解”“例析圖形，提升能力”四個方面展開教學與分析.

[ 關鍵詞 ]圖形；解題；教學

學生通過學習要掌握且能應用一些基本圖形來解決問題.教師在實施教學時要有意識地強化學生對圖形的應用意識，引導學生從基本圖形中發現問題、描述問題，以發展空間想象力.為此，筆者在初三復習階段，對基本圖形進行了探索，對利用基本圖形提升數學解題能力展開了教學與研究.本文以“兩相等線段共用一端點”的復習教學為例展開闡述.

開門見山，揭露主題

如圖1，線段AB，AC擁有一個公共的端點A，形成∠BAC，本節課就以這個常見圖形為例，展開對基本圖形的專題復習.

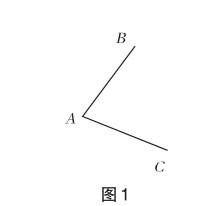
設計意圖 這是一個常考常新的基本圖形，在日常練習或檢測中比較常見，本節課以此為專題復習的起點，門檻較低，便于各個認識水平層次學生的理解.

借助圖形，夯實基礎

教學設想 引導學生從這個基本圖形出發展開聯想，發現含有該結構的簡單圖形，分析圖形間的異同點，增強對圖形關聯性的認識，以提升解題能力與空間想象力.經交流，學生列舉出如下含有該基本圖形結構的常見圖形：①含有中點的線段；②等邊、等腰三角形；③正方形、菱形；④扇形.如圖2，扇形比較特殊，它是在圖1的基礎上增加了一條曲線.

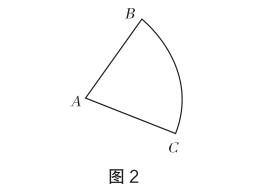
設計意圖 要求學生自主總結包含“兩條相等線段共用一端點”的基本圖形，為接下來的復習專題研究奠定基礎，并特別強調扇形的特殊性，以發展學生的歸類能力，讓學生感悟從特殊到一般的數學思想.

應用圖形，深化理解

之前在學習基本圖形時，教師并沒有將具有特殊結構的圖形作為教學的重點，所以大部分學生都沒有深入探索過這些特殊圖形.復習教學時，教師可帶領學生適當地增加對特殊圖形的研究，以拓寬學生的視野，深化學生對平面幾何的理解.如箏形、對角互補的四邊形等.

例1 如圖3，在四邊形ABCD中，AB=BC，AD=2，CD=4，∠B=∠D=90°，則BD的長是多少？

將“相等線段共用同一端點”這個結構應用到對角互補的四邊形中，可讓學生對對角線與邊長的關系產生深刻認識.因此，這是一個值得探索的問題.

為了引發學生對該基礎圖形的認識，筆者由淺入深地設計了問題串，以啟發學生的思維.

問題1 從動態的角度來觀察上述圖形的構造（即延長DC至點E，使AD=EC），圖形發生了什么變化？

預設：可將△BEC視為△BDA圍繞點B旋轉之后而獲得的.

問題2 圖3中存在“兩條等長線段共用一個端點”的基本結構嗎？該結構在解決問題中起到了怎樣的作用？

問題3 問題中所提到的四邊形對角互補具有怎樣的作用？

預設：∠BCE=∠BAD.

問題4 通過以上分析可以發現，圖形位置的變化，有效啟發了我們的思維，若一開始我們就從旋轉的角度來分析問題，那么在本題中旋轉的契機在哪兒？

預設：因為明確存在“相等線段共用一個端點”的基本結構，因此可視為將BA圍繞點B旋轉到BC，同時△BDA則旋轉到△BEC的位置.

問題5 點E為什么落在了DC的延長線上呢？

預設：因為∠BAD和∠BCD是互補的關系，因此∠BAD的對應角∠BCE和∠BCD為互補的關系.

問題6 由圖形位置變化可發現新圖形的產生，具體會產生什么新的圖形呢？

預設：△DBE為等腰直角三角形.

問題7 你是如何獲得∠EBD= 90°這個結論的？

預設：根據AB與BC的夾角為90°而得.

設計意圖 “兩相等線段共用同一端點”的基本結構為學生展示了動態變化的多種可能，而圖形位置的變化則帶來了更多新的解題思路，讓解題獲得了多種可能.兩條線段夾角度數問題對新的圖形中的角具有直接影響，因此可以此作為模型為后續例題教學服務.

例析圖形，提升能力

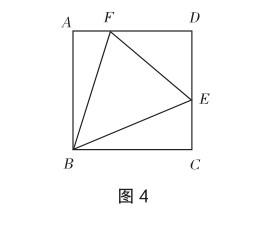
例2 如圖4，若點E，F分別為正方形ABCD的邊DC，AD上的點，已知CE+AF=EF，那么∠EBF的度數是多少？

為了讓學生充分認識到本節課所探索的基本圖形具有怎樣的作用，教師可設置一些復雜的圖形，鼓勵學生從中探尋基本圖形.如對于例2，就能從與正方形結合的圖形中發現基本圖形.

例3 如圖5，△ABC為一個等腰直角三角形，且D是斜邊AC上一點，那么AD，BD，CD之間存在怎樣的數量關系？

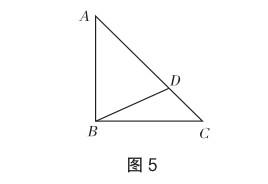
除此之外，教師還可以引導學生從類似結構（等腰直角三角形）中發現端倪，以提高學生的空間想象力，或通過變化兩線段夾角的大小，引導學生觀察并總結新圖形中角度的變化情況.

例5 如圖7，已知△ABC中的∠A為直角，D是BC邊的中點，且DE⊥DF，DE與AB相交于點E，DF與AC相交于點F，分析線段EB，EF，FC之間存在怎樣的數量關系，并說明理由.

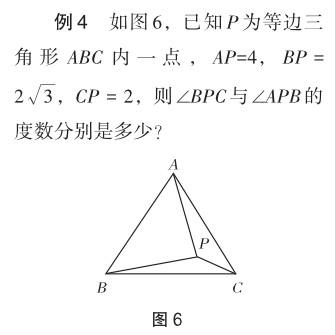
例7 如圖9，已知△ABC為⊙O的內接等邊三角形，P為圓上一動點，請證明：AP = BP + CP.

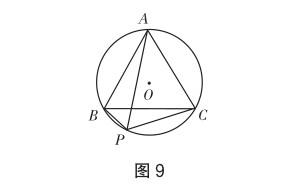
例8 （去除常見圖形） 如圖10，已知△ABC中的AB邊與AC邊相等，將線段BC圍繞著點B逆時針旋轉60°，可得線段BD，若∠ABE= 60°，∠BCE=150°：

（1）請判斷△ABE為怎樣的一個三角形，并證明；

（2）連接DE，若明確∠CED= 45°，則∠BAC的度數是多少？

設計意圖 例8去掉了等邊三角形，只留下了最基本的圖形結構，將結構的核心凸顯出來.如此設計，是為了進一步強化“兩相等線段共用同一端點”這個基本圖形在解題中的重要性.

結語

幾何是發展學生空間想象力的基礎，也是初中數學教學的重點與難點內容之一.事實證明，任何一個復雜圖形都是由最基本的圖形經過變式而來的，引導學生建立基本圖形，并從中抽象模型對鍛煉學生的解題能力與數學思維具有深遠的影響.

本節課作為初三復習中的一次嘗試，筆者從專題的角度帶領學生由淺入深地分析基本圖形，不僅有效提高了復習成效，還顯著加強了復習內容的綜合性與關聯性.學生通過對基本圖形的提煉、應用、感悟，進一步拓寬了視野，發現了解決問題的本質.