走進多函數幾何，方法探究總結

曹玉利

[ 摘 要 ]多函數幾何綜合是中考的重點和難點問題，常作為壓軸題出現，可綜合考查學生的基礎知識與綜合能力.探究解析時需要把握知識關聯點，數形結合解析函數與圖象，提取模型轉化條件.多函數綜合題的解析思路十分重要，文章結合實例開展探究總結.

[ 關鍵詞 ]多函數；數形結合；圖象

問題探究

1.問題呈現

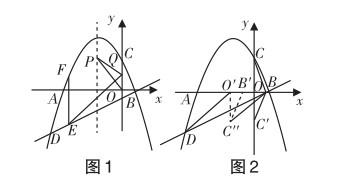
（1）求直線BD的解析式；

（2）E是線段BD上的一個動點，過點E作x軸的垂線交拋物線于點F，當折線EF+BE最大時，在拋物線對稱軸上找一點P，在y軸上找一點Q，連接QE，OP，PQ，求OP+PQ+QE的最小值；

（3）如圖2，連接BC，把△OBC沿x軸翻折，翻折后的△OBC記為△OBC′，現將△OBC′沿著x軸平移，平移后△OBC′記為△O′B′C″，連接DO′，C″B，記C″B與x軸形成的較小夾角度數為α，當∠O′DB=α時，求出此時點C″的坐標.

2.考點解析

上述為拋物線綜合題，涉及函數與幾何的相關知識，可歸為多函數幾何綜合題，即包括了二次函數與一次函數的相關知識.題設三問，每問各自獨立又具有一定的關聯，探究解析時要深入解讀條件，結合圖象分析.

第（1）問求解直線BD的解析式，考查待定系數法.

第（2）問求解線段和的最小值，為線段最值問題.題干設定動點，構建折線，涉及點的對稱，考查對稱轉化、動點模型構建等知識.

第（3）問求解點的坐標，涉及三角形翻折、平移等知識，屬于幾何動態問題，考查幾何翻折、平移特性，函數背景下的幾何動態分析轉化是破題的關鍵.

3.思路突破

對于多函數幾何綜合題，可以采用分步突破的策略，即對特定問題條件進行針對性解析，把握關鍵信息，構建模型，逐步突破，下面具體探究.

第一步，待定系數求解析式

第（1）問求解直線BD的解析式，可先求出點B，D的坐標，假設出直線BD的解析式，再分別代入即可求解.

②線段和最值求解：如圖4所示，作點E關于y軸的對稱點N，EM⊥AB于點M，連接MN，交對稱軸于點P，交y軸于點Q.由于點M，O關于對稱軸對稱，可得OP=PM.又知點E和點N關于y軸對稱，則QE= QN，所以有OP + PQ + QE = PM + PQ + QN.

解后探究

上述基于一道函數與幾何綜合題開展解題探究，其中問題涉及多函數，主要探究二次函數與一次函數的圖象，分析拋物線與直線的位置關系.其中后兩問是問題的核心之問，解析過程與探究思路具有一定的參考價值，下面進一步探究解法.

1.關于第（2）問的解法探究

問題的第（2）問探究線段和最值，涉及三條線段，解題的核心知識是“兩點之間，線段最短”，即構建線段共線，確定最值情形.上述解析的關鍵有兩點：一是推導關鍵點的坐標，構建三角函數模型，借助三角函數來推導幾何角，求出兩線段和的最值，確定關鍵點的坐標；二是開展對稱轉化，構建線段共線，確定最值情形.

后續對于與線段和相關的最值問題，可按照如下步驟進行思路構建：

第一步，數形結合分析函數圖象之間的位置關系，把握其中的幾何特性；

第二步，充分提取圖象中的幾何模型，如相似模型、直角三角形模型、全等模型，進行線段關系轉化；

第三步，把握線段的位置關系，開展對稱轉化，分析共線條件，構建共線模型，確定線段最值情形，完成求解.

2.關于第（3）問的解法探究

問題的第（3）問探究幾何運動中點的坐標，其中三角形經歷了翻折與平移，需要從“數”與“形”雙重視角解讀其中的幾何運動.即翻折與平移過程中圖形的形狀并未發生變化，同時函數的解析式存在一定的關聯.上述解析的關鍵有兩點：一是把握翻折與平移的幾何特性，推導幾何條件；二是提取其中的相似模型，基于相似三角形對應邊成比例構建方程，解方程求點的坐標.

后續對于與幾何運動相關的綜合問題，可按如下步驟進行思路構建：

第一步，理解幾何運動過程，基于運動規律推導幾何條件；

第二步，整合幾何條件，提取其中的幾何模型，挖掘隱含條件；

第三步，數形結合分析和轉化條件，構建思路解題.

3.關于多函數綜合題的解題策略總結

多函數綜合常作為壓軸題在中考中出現，通常融合一次函數、反比例函數與二次函數中的兩種或三種，具體解析時要把握函數的圖象和性質，逐步推理解析，有如下三種破解策略.

策略1：數形結合解析.對于多函數幾何問題，可采用數形結合的分析策略，即審題、讀題、理解圖象，把握圖象挖掘隱含條件，利用圖象模型來轉化條件.

策略2：把握對應關系.函數解析式與圖象之間存在一定的關聯，探究解析時可從“數”與“形”兩個視角來解讀.如聯立函數解析式構建方程，所求點的坐標即為函數圖象的交點，解的個數即為交點的個數.也可反向利用交點個數來解析方程解的個數.

策略3：提取模型簡化.多函數幾何問題的綜合性強，解題時可以采用模型提取的方式，即簡化圖象，提取特殊模型，利用模型來轉化條件.如提取圖象中的全等或相似模型，直角三角形或等邊三角形模型，利用模型特性來分析與轉化條件.

拓展探究

上述總結了多函數問題的解題策略，以及典型問題的解題方法，下面結合實例進一步探究，強化解法，積累解題方法.