抑制抖振的PMSM無位置傳感器控制算法優化

摘 "要： 在分析無位置傳感器控制永磁同步電機（PMSM）發生高頻抖振原因的基礎上，文中提出對PMSM滑模觀測器算法及起動控制進行優化，包括：使用雙曲正切函數代替符號函數作為滑模面切換函數，基于李雅普諾夫理論的滑模增益整定，使用鎖相環法代替反正切法估計轉子位置等。針對PMSM全速域無位置傳感器運行時電機低速起動位置估計困難的問題，提出恒電流頻比（[IF]）控制。考慮零速起動的PMSM由[IF]控制轉向滑模觀測器控制切換時產生的電磁轉矩不平穩，引入避免滑模觀測器給定觀測位置角差值發生波動的[q]軸電流系數，并制定轉子電流控制新策略。仿真實驗結果證明該方法相比傳統方法能有效降低轉速波動且轉子位置角估算誤差更小，驗證了所提優化方法在抑制抖振方面的有效性。該算法可應用于智能制造領域，以有效抑制系統抖振問題，進而提升智能制造企業生產效益。

關鍵詞： 永磁同步電機； 無位置傳感器控制； 滑模觀測器； 抖振抑制； 恒電流頻比； 全速域

中圖分類號： TN609?34 " " " " " " " " " " " " "文獻標識碼： A " " " " nbsp; " " " " " " " 文章編號： 1004?373X（2024）21?0125?06

Optimization of position sensorless control algorithm for PMSM to suppress chattering

LUO Shuai1， 2， ZHANG Liangli1， 2， XU Wanwan1， 2， GONG Ruohan1， 2， WU Meiqin1， 2

（1. School of Information Science and Engineering， Wuhan University of Science and Technology， Wuhan 430081， China;

2. Engineering Research Center for Metallurgical Automation and Measurement Technology of Ministry of Education，

Wuhan University of Science and Technology， Wuhan 430081， China）

Abstract： An optimization of the sliding mode observer algorithm and starting control of PMSM （permanent magnet synchronous motor） are proposed based on the cause analysis of the high?frequency chattering of the PMSM with position sensorless control. The optimization includes the following three aspects. The hyperbolic tangent function is used to replace the sign function and is taken as the sliding surface switching function. The sliding mode gain setting is performed based on the Lyapunov theory. The phase?locked loop method is used to replace the arc tangent method for the estimation of motor rotor position. In view of the fact that it is difficult to estimate the position of motor starting at low speed when PMSM is running with position sensorless in full speed domain， the constant current intensity?frequency （[IF]） ratio control is proposed. Considering that the electromagnetic torque of PMSM with zero?speed starting is unstable when it is switched from [IF] control to sliding mode observer control， a [q]?axis current coefficient is introduced to avoid the fluctuation of the angle difference between the given and observed position of sliding mode observer， and a new rotor current control strategy is designed. The simulation results show that the proposed method can reduce the speed fluctuation effectively and the estimation error of rotor position angle is smaller than that of the traditional method， so the effectiveness of the proposed optimization method in suppressing chattering is verified. The algorithm can be applied to the field of intelligent manufacturing to suppress the system chattering effectively， and then improve the production efficiency of the intelligent manufacturing enterprises.

Keywords： PMSM; position sensorless control; sliding mode observer; chattering suppression; I/F; full speed domain

0 "引 "言

永磁同步電機（Permanent Magnet Synchronous Motor， PMSM）無位置傳感器控制算法中，反電勢積分法易受電機參數變化的影響，且存在定子磁鏈積分的常值漂移問題[1?2]；模型參考自適應算法對參數變化比較敏感[3]；擴展卡爾曼濾波器算法實時計算量大，對控制芯片依賴度高，動態響應不理想[4?5]；滑模觀測器算法響應迅速，對系統內部參數變化和外部擾動不敏感，計算簡單、易于實現[6?7]。

采用無位置傳感器控制的PMSM易發生高頻抖振。主要原因在于滑模觀測器常采用不當的切換函數，加上滑模增益常根據設計人員經驗定參，且轉子位置估計采用開環系統測算，使抖振誤差進一步放大，長期處于抖振狀態的PMSM不利于智能制造企業生產效益提升[8]。

優化使用滑模觀測器的PMSM無位置傳感器控制，可從切換函數、滑模增益定參和轉子位置估計三方面進行。為避免PMSM在零速起動時的反電動勢信息無法被滑模觀測器獲取并轉換為有效的轉子位置信息，PMSM起動控制策略需做相應調整，設計合理的轉子電流配給方法，使其平穩切換至滑模觀測器控制模式，保障在全速域范圍內穩定運行。

1 "問題分析

1.1 "滑模觀測器

PMSM在靜止坐標系[α?β]下的數學模型為：

[ddtiαiβ=-RsLiαiβ+1Luαuβ-1Leαeβ，eαeβ=ψfωe-sinθecosθe] （1）

式中：[uα "uβT]、[iα "iβT]、[eα "eβT]分別為[α?β]坐標系下的定子電壓、電流、反電動勢；[θe]為轉子位置角；[Rs]為定子電阻；[ωe]為電角速度；[L]為定子繞組電感；[ψf]為永磁體磁鏈。

在靜止坐標系下，滑模觀測器數學模型如下：

[ddtiαiβ=-RsLiαiβ+1Luαuβ-1LkZ] （2）

式中：[iα]、[iβ]分別為[α]軸、[β]軸定子電流觀測值；[k]為滑模增益；[Z]為切換函數。

滑模面選取觀測值與實際值之差，其表達式為：

[s=sαsβ=iα-iαiβ-iβ] （3）

由式（1）～式（3）可得滑模觀測器動態誤差方程為：

[ddtsαsβ=-RsLsαsβ-1LkZ+1Leαeβ] （4）

滑模觀測器的滑模面切換函數選定后，滑模增益[k]值的選取通常根據設計經驗試探性取值，然后根據系統輸出情況調整。

系統進入滑模面后，將[s=s=0]代入式（1）可得：

[kZ=eαeβ=ψfωe-sinθecosθe] （5）

由式（5）可知，控制信號[kZ]中包含PMSM反電動勢信息。對該控制信號進行濾波處理，可得到反映轉子位置信息[θe]的反電動勢觀測值[eα]、[eβ]，有：

[eαeβ=kZωcs+ωc] （6）

式中[ωc]為濾波器截止頻率，后續常采用解析幾何算法來估計轉子位置。為防止角度觀測值存在相位延遲，利用轉速觀測值[ωe]和低通濾波器截止頻率[ωc]對角度觀測值[θe]進行補償，有：

[θe=-arctaneαeβ+arctanωeωc] （7）

1.2 "抖振原因分析

1.2.1 "切換函數存在跳躍間斷點

傳統滑模觀測器采用符號函數[sgn（s）]作為切換函數，如圖1a）所示。

[sgn（s）]為非線性函數，且在[s=0]處的跳躍間斷點會引起系統在滑模面附近產生高振幅振蕩。

1.2.2 "滑模增益[k]值選取不當

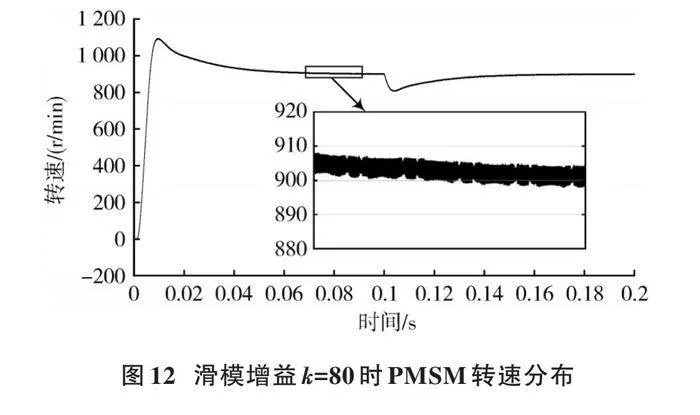
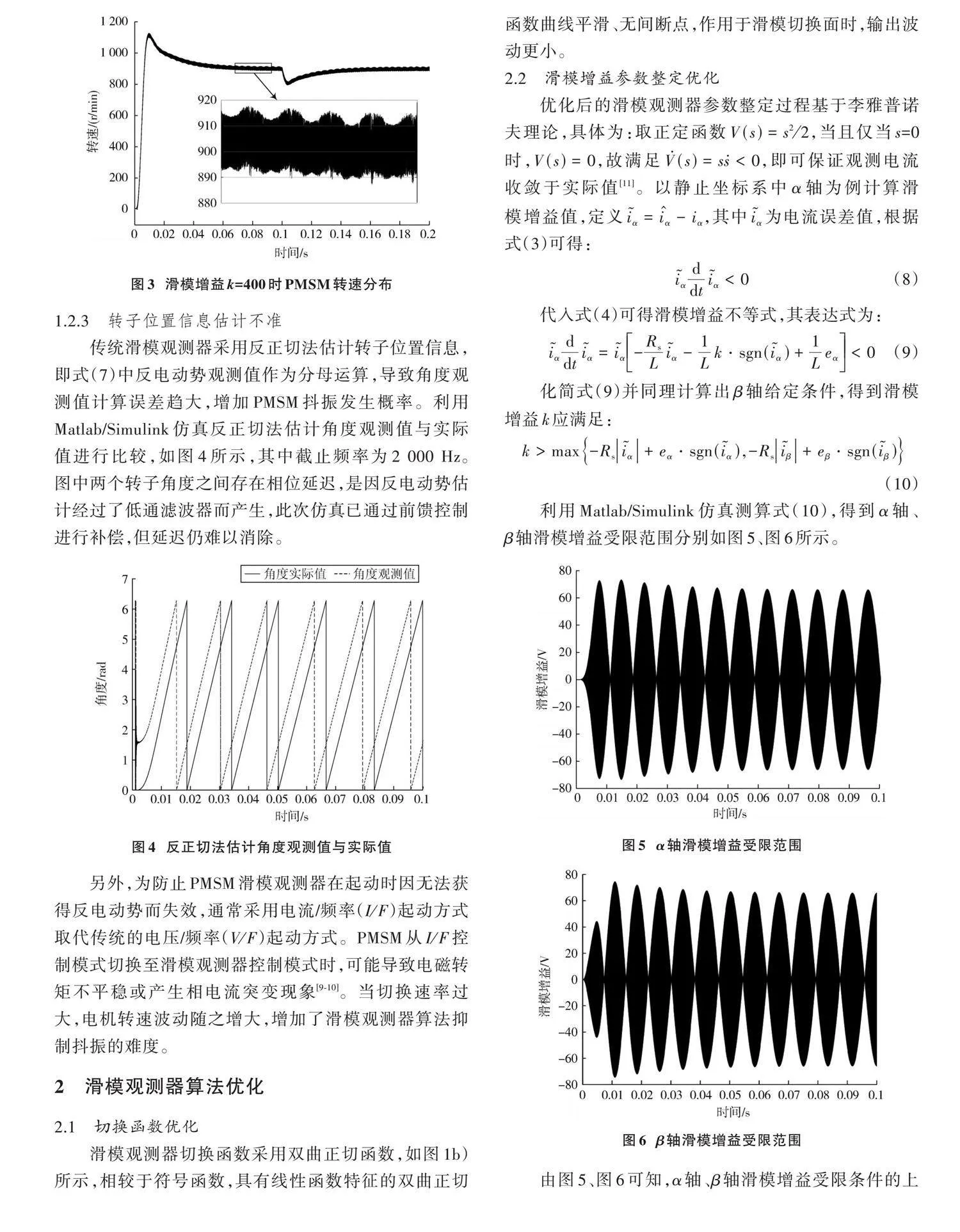
利用Matlab/Simulink仿真PMSM運行至0.1 s時突增5 N·m載荷，在不同滑模增益[k]值下，PMSM轉速分布如圖2、圖3所示。當滑模增益選取過小（[k]=40）時，會導致滑模觀測器觀測結果發散，PMSM無法到達期望轉速900 r/min；選取過大（[k]=400）時，PMSM雖能達到期望轉速值，但在其附近大幅度波動且抖振頻率較高。

1.2.3 "轉子位置信息估計不準

傳統滑模觀測器采用反正切法估計轉子位置信息，即式（7）中反電動勢觀測值作為分母運算，導致角度觀測值計算誤差趨大，增加PMSM抖振發生概率。利用Matlab/Simulink仿真反正切法估計角度觀測值與實際值進行比較，如圖4所示，其中截止頻率為2 000 Hz。圖中兩個轉子角度之間存在相位延遲，是因反電動勢估計經過了低通濾波器而產生，此次仿真已通過前饋控制進行補償，但延遲仍難以消除。

另外，為防止PMSM滑模觀測器在起動時因無法獲得反電動勢而失效，通常采用電流/頻率（[IF]）起動方式取代傳統的電壓/頻率（[VF]）起動方式。PMSM從[IF]控制模式切換至滑模觀測器控制模式時，可能導致電磁轉矩不平穩或產生相電流突變現象[9?10]。當切換速率過大，電機轉速波動隨之增大，增加了滑模觀測器算法抑制抖振的難度。

2 "滑模觀測器算法優化

2.1 "切換函數優化

滑模觀測器切換函數采用雙曲正切函數，如圖1b）所示，相較于符號函數，具有線性函數特征的雙曲正切函數曲線平滑、無間斷點，作用于滑模切換面時，輸出波動更小。

2.2 "滑模增益參數整定優化

優化后的滑模觀測器參數整定過程基于李雅普諾夫理論，具體為：取正定函數[V（s）=s22]，當且僅當[s]=0時，[V（s）=0]，故滿足[V（s）=sslt;0]，即可保證觀測電流收斂于實際值[11]。以靜止坐標系中[α]軸為例計算滑模增益值，定義[iα=iα-iα]，其中[iα]為電流誤差值，根據式（3）可得：

[iαddtiαlt;0] （8）

代入式（4）可得滑模增益不等式，其表達式為：

[iαddtiα=iα-RsLiα-1Lk?sgn（iα）+1Leαlt;0] （9）

化簡式（9）并同理計算出[β]軸給定條件，得到滑模增益[k]應滿足：

[kgt;max-Rsiα+eα?sgn（iα），-Rsiβ+eβ?sgn（iβ）]

（10）

利用Matlab/Simulink仿真測算式（10），得到[α]軸、[β]軸滑模增益受限范圍分別如圖5、圖6所示。

由圖5、圖6可知，[α]軸、[β]軸滑模增益受限條件的上限值均低于80，選定滑模增益[k]值為80能夠使系統穩定。

2.3 "估計轉子位置方法優化

優化滑模觀測器轉子位置估計采用鎖相環（PLL）法。相較于反正切法，PLL法無除法運算，且為閉環系統，如圖7所示。圖中[eα]、[eβ]同式（6），通過PI控制器可使滑模觀測器輸出和實際位置誤差趨近于0，其等效傳遞函數方框圖如圖8所示。

圖8中，[θe]、[ωe]同式（7），[Kp]、[Ki]分別為PLL中PI控制器的比例、積分增益。

依據傳遞函數方框圖得到系統閉環傳遞函數為：

[θeθe=ωeψfKps+ωeψfKis2+ωeψfKps+ωeψfKi] （11）

根據經典控制理論，式（11）的特征根極點均分布在復平面左半平面，表明系統穩定，且對于I型系統的階躍響應，其穩態誤差[ess=0]。

2.4 "[IF]控制切換至滑模觀測器控制優化

PMSM采用[IF]起動控制模式（電流閉環+速度開環）向滑模觀測器控制（電流、速度雙閉環控制）切換時，電流存在幅值差，此為導致電磁轉矩不平穩和相電流突變等現象的直接原因[12]。利用切換前后的轉子電角度差作為減小[q]軸電流的參考變量，可有效降低因切換前后電流幅值差產生的影響。

PMSM轉矩方程為：

[Te=1.5pnIsψfsinδ] （12）

式中：[Te]為電磁轉矩；[pn]為電機磁極對數；[Is]為定子電流；[δ]為電機功角。

設[IF]起動給定位置角為[θ*]，滑模觀測器觀測位置角為[θsmo]，兩者相差的電角度[θerr]為：

[θerr=θsmo-θ*=π2-δ] （13）

因此，通過對[θerr]反饋調節來減少給定定子電流[Is]，繼而使[θerr]自身減小，達到同步減小給定定子電流[Is]和角度差[θerr]的目的，最終收斂到[Id]=0控制點，此時[Is]=[Iq]。根據式（12），給定定子電流在[q]軸上分量[Iq]與角度差[θerr]的關系為：

[Iq=Te1.5pnψfcosθerr] （14）

式中[Iq]與[θerr]成正比。傳統處理方法是：當[θerr]降至0值時，會在0值附近波動，當[θerr]小于等于某一較小閾值[ε]的次數達到設定次數時，完成切換。若此時切換不及時，可能導致電流小幅波動，系統發散[13?14]。優化措施是：引入[q]軸電流系數[ke]，可避免[θerr]在0值附近出現波動現象，此時[θerr]以“先快后慢”的形式趨近于0，[ke]的表達式為：

[ke=λ2πθerrn， " "n=1，2，3，…] （15）

當[n]、[λ]選定后，[θerr]較大時，[ke]隨之變大，其調節[q]軸電流減小得越快；當[θerr]較小或接近0時，其調節[q]軸電流減小得越慢。[λ]值決定系數[ke]的作用范圍，[n]值選取越大，系數[ke]作用越明顯。

3 "仿真驗證

利用Matlab/Simulink構建基于[IF]起動并可切換至滑模觀測器的PMSM無位置傳感器控制系統，如圖9所示。其中，PMSM參數設置為：極對數[pn]=4，定子電感[L]=8.5 mH，定子電阻[Rs]=2.875 Ω，磁鏈[ψf]=0.175 Wb，轉動慣量[J]=0.001 kg·m2，阻尼系數[B]=0.008，直流母線[Udc]=311 V，PWM開關頻率[fPWM]=10 kHz，[IF]起動給定的頻率加速度[af]=30 Hz/s2，初始給定電流為10 A，角度差反饋調節參數取[n]=3、[λ]=2，滑模觀測器輸入為電機靜止坐標系下定子電壓和定子電流，輸出為估計電角速度和轉子估計位置。

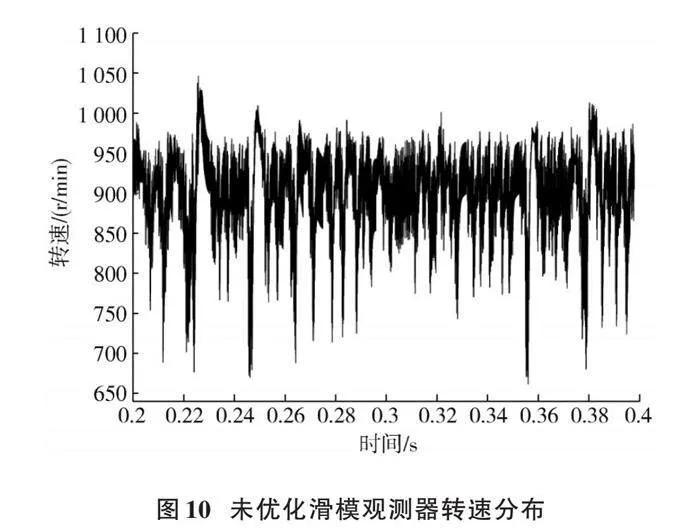
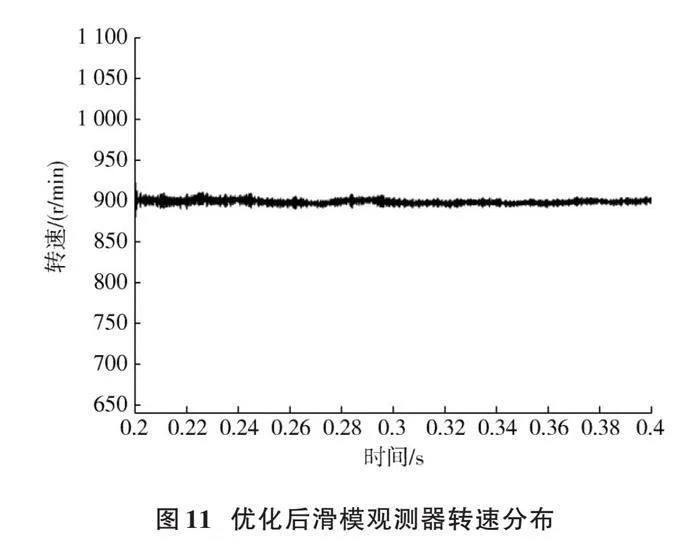
圖10、圖11分別為滑模觀測器采用符號函數和雙曲正切函數時觀測轉速分布圖。相較于未優化，優化后的滑模觀測器轉速抖振抑制效果更加明顯。

滑模增益選取優化后的PMSM轉速分布，如圖12所示。與圖2（滑模增益[k]=40）相比，圖12（滑模增益[k]=80）中PMSM轉速能快速收斂于期望值；與圖3（滑模增益[k]=400）相比，圖12中PMSM轉速抖振振幅更小。表明滑模增益參數整定過程優化有效。

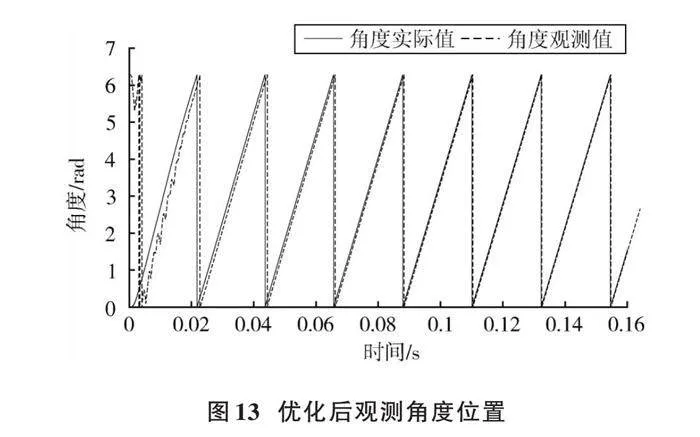
PMSM滑模觀測器采用PLL法估計轉子位置，得出角度觀測值與實際值之間的對比如圖13所示。在初動階段，估計結果仍存在誤差，但因PLL法所具有的閉環結構，在PMSM轉子經過4轉后，角度觀測值誤差趨近于0。與圖4所示反正切法估計角度觀測值相比，優化后的PMSM轉子位置信息在精準度和響應速度方面有明顯提升。

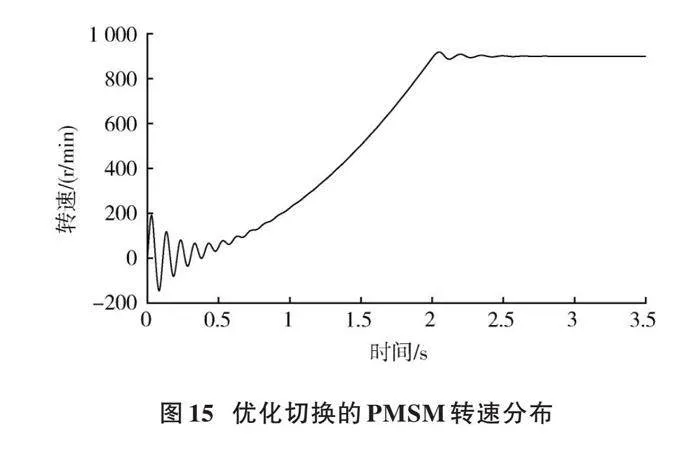
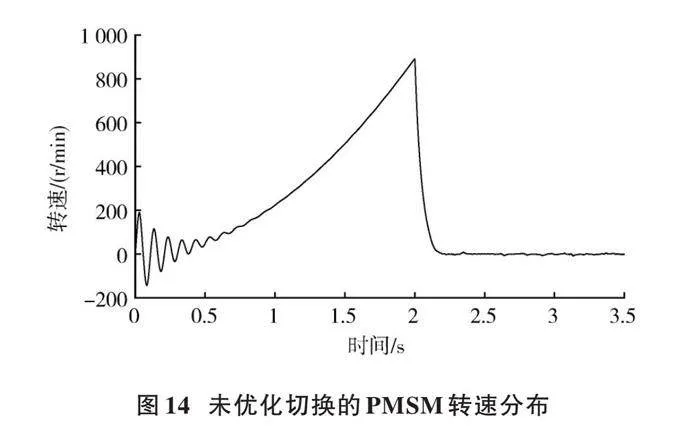
設定PMSM采用[IF]控制零速起動，至900 r/min時，自動切換至滑模觀測器控制。未經優化的切換動作后，電機轉速變化如圖14所示，從高值急劇下降至0，表明電機控制已失效，切換失敗。同等條件下使用優化的切換方式，電機轉速變化如圖15所示，在切換點短時小幅波動后電機即進入平穩段，轉速最終維持在900 r/min左右，表明電機已從[IF]起動控制模式平順切換至滑模觀測器控制模式。

4 "結 "語

本文分別對構建滑模觀測器的滑模面切換函數、滑模增益選取、轉子位置估計三個環節進行機理分析，得出傳統滑模觀測器建模方法致使無位置傳感器控制PMSM發生抖振的原因所在，并對應提出優化方法。考慮到零速起動的PMSM在由[IF]控制向滑模觀測器控制切換時，可能發生失效問題，因此引入[q]軸電流系數，平抑[IF]起動給定位置角與滑模觀測器觀測位置角之間的差值波動，使電機平穩切換至滑模觀測器控制模式。仿真結果表明，經過各層面多角度優化，無位置傳感器控制PMSM從零速到高速值運轉切換平穩，轉速波動小，系統抖振問題得到有效抑制。

參考文獻

[1] 張祺琛，劉細平，王方凱文，等.基于改進滑模觀測器的永磁同步電機無傳感器控制[J].組合機床與自動化加工技術，2022（1）：85?88.

[2] PENG Y， YIN Y C， WANG X J， et al. PMSM torque ripple minimization based on novel low carrier ratio PWM technique [J]. IEEE transactions on power electronics， 2022， 37（9）： 11071?11084.

[3] 趙毅恒，寧博文，盧少武，等.基于[IF]起動和擴展卡爾曼濾波的永磁同步電機全速域無傳感器控制方法[J].電機與控制應用，2022，49（2）：1?7.

[4] 于安博，劉利，闞志忠，等.高頻脈振信號注入永磁同步電機無濾波器初始位置辨識方法[J].電工技術學報，2021，36（4）：801?809.

[5] ISMAL M M， XU W， GE J， et al. Adaptive linear predictive model of an improved predictive control of permanent magnet synchronous motor over different speed regions [J]. IEEE transactions on power electronics， 2022， 37（12）： 15338?15355.

[6] 王要強，朱亞昌，馮玉濤，等.永磁同步電機新型趨近律滑模控制策略[J].電力自動化設備，2021，41（1）：192?198.

[7] WANG F， WANG J M， WANG K， et al. Adaptive backstepping sliding mode control of uncertain semi?strict nonlinear systems and application to permanent magnet synchronous motor [J]. Journal of systems science amp; complexity， 2021， 34（2）： 552?571.

[8] XU J Q， JIN W B， HONG G， et al. Modeling and analysis of oil frictional loss in wet?type permanent magnet synchronous motor for aerospace electro?hydrostatic actuator [J]. Chinese journal of aeronautics， 2023， 36（11）： 328?341.

[9] CHOO K M， WON C Y. Flying start of permanent?magnet?synchronous?machine drives based on a variable virtual resistance [J]. IEEE transactions on industrial electronics， 2020， 68（10）： 9218?9228.

[10] 章春娟，王慧貞，劉偉峰，等.基于寬頻帶同步基頻提取濾波器的永磁同步電機轉子位置與轉速估計[J].電工技術學報，2022，37（4）：882?891.

[11] 董鋒斌，劉昌建，趙永瑋，等.基于擴張狀態觀測器的DFIG網側變換器滑模控制[J].電力工程技術，2023，42（2）：206?214.

[12] 肖仁鑫，沈培航.永磁同步電機全速域無位置傳感器復合控制[J].組合機床與自動化加工技術，2022（11）：79?83.

[13] 周濤，蔣全.無傳感器永磁同步電機全速范圍控制技術綜述[J].電子科技，2021，34（4）：59?69.

[14] 吳春，傅子俊，孫明軒，等.基于擴張狀態觀測器負載轉矩補償的永磁同步電機全速范圍無位置傳感器控制[J].電工技術學報，2020，35（z1）：172?181.

作者簡介：羅 "帥（1999—），男，湖北天門人，碩士研究生，研究方向為永磁同步電機無傳感器控制。

張良力（1981—），男，湖北武漢人，博士研究生，副教授，主要從事電氣工程及其自動化專業的教學與科研工作。