2023年全國乙卷理科第10題的解法、變式與推廣

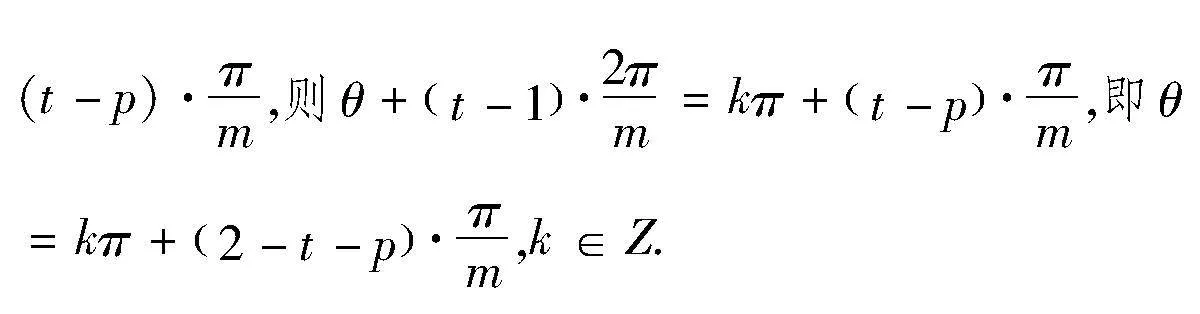
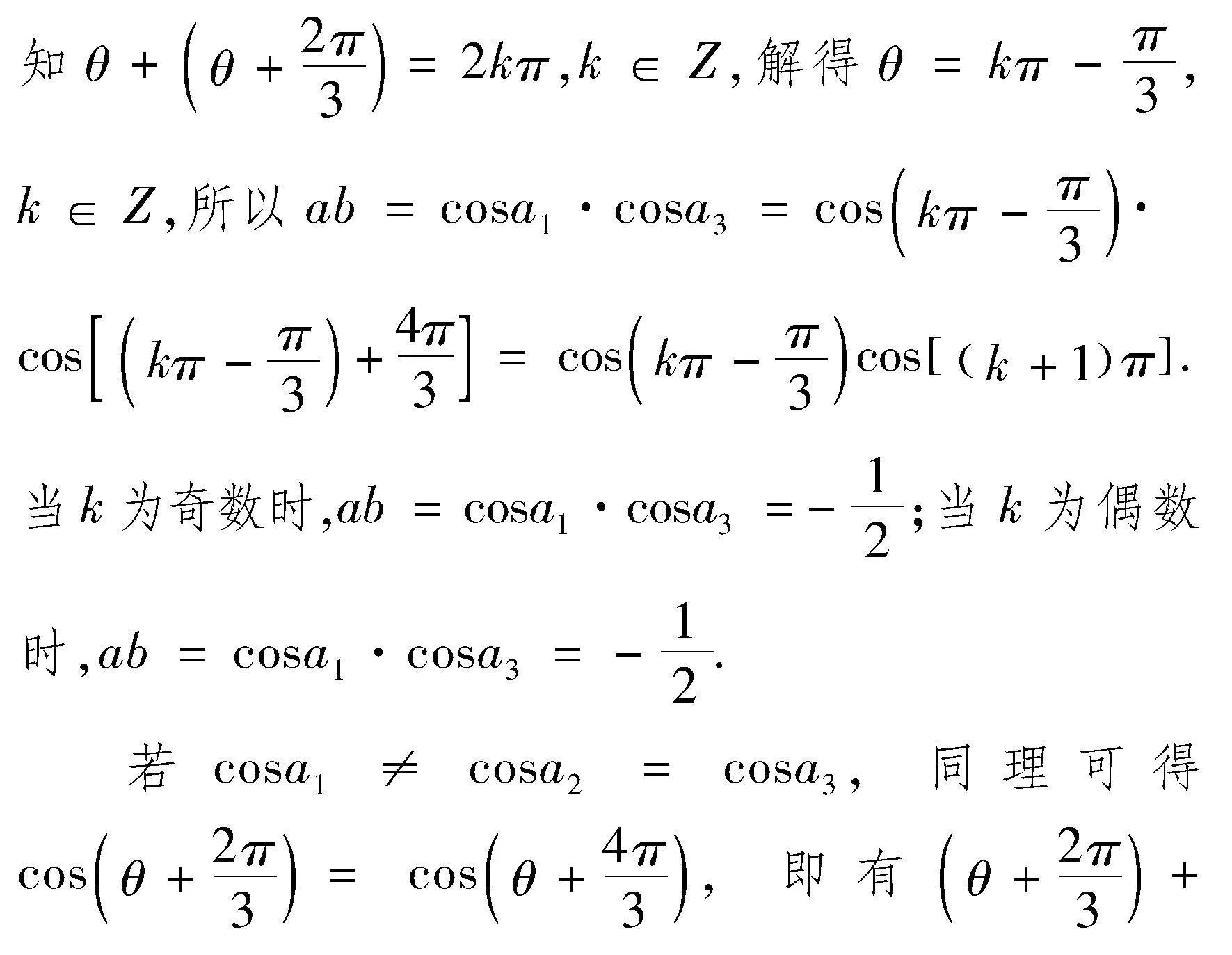
1.真題再現

該題以等差數列為背景，考查三角函數周期性與數列的函數本質.先表示出等差數列的通項公式，求得函數y=cosan的周期為3，獲得函數的值域最多含有3個數，再根據集合元素的互異性確定函數值.

2.解法探究

思路1 利用三角函數的周期性

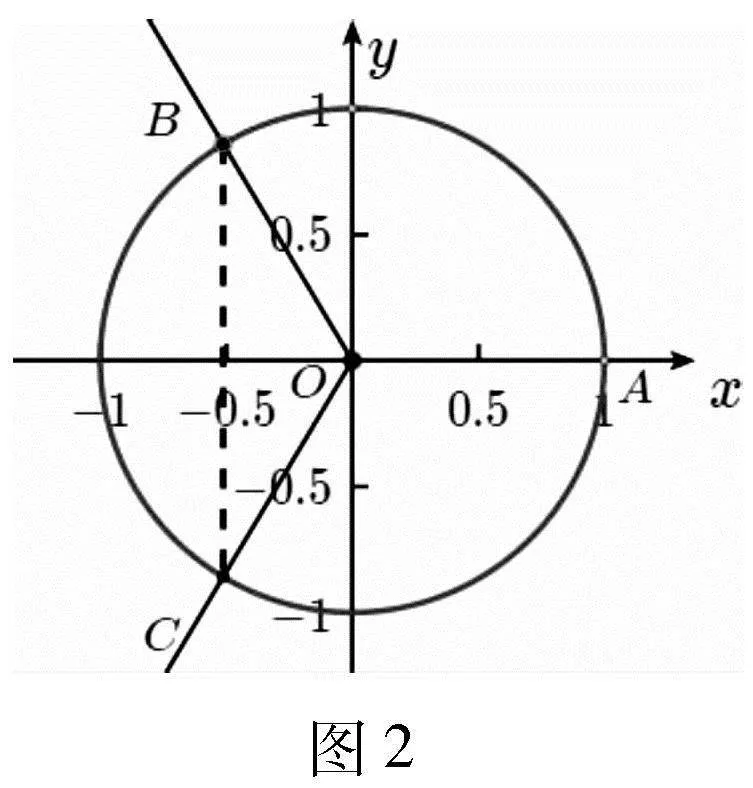
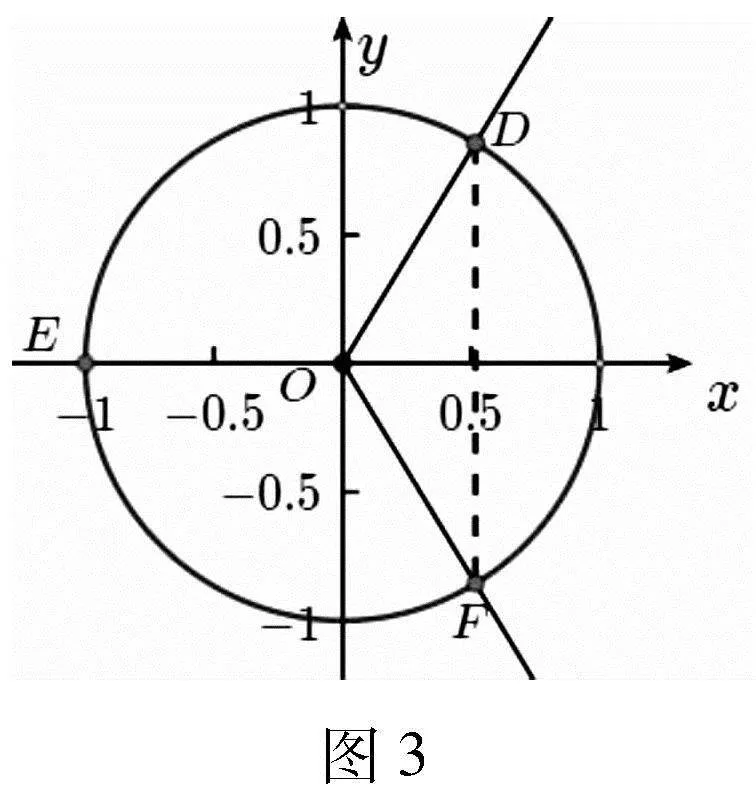
思路2 利用單位圓，數形結合.

解法2：由解法1可知cosa1，cosa2，cosa3中，cosa1=cosa2≠cosa3或cosa1≠cosa2=cosa3.

思路3 利用特殊值.

此題的設計創新點在于將函數的周期與等差數列相結合，三角函數的所有正周期按照由小到大順序排列就是一個等差數列，而數列的本質也是函數，從而獲得一個定義域為正整數的復合函數的值域問題，解法1主要是根據函數周期和值域S中元素個數建立三角方程，利用余弦曲線求解等差數列的首項，從而獲得等差數列通項. 解法2是根據在單位圓中角α余弦的定義直觀觀察出a，b的值.

本題源于課本中等差數列的概念和等差數列的通項公式，以及三角函數的周期性，涉及數學抽象和數學運算等素養.數列問題可以從特殊到一般，也可以從一般入手研究數列的前幾項，從而得到規律. 解決數列問題的關鍵是歸納、猜想、證明.

3.背景分析

4.變式及推廣

解：根據周期為5，由集合S元素的個數必有數列{an}前五項中兩項終邊關于x軸對稱且一項終邊在x上，所以5項正弦和為0，即T2025=0.

參考文獻

［1］教育部教育考試院.深入考查基礎知識和能力 助力人才選拔和“雙減”落地——2023年高考數學全國卷試題評析［J］.中國考試，2023（07）：15-21.