例題教學的改進與思考

劉曉龍

摘要：數學教學離不開例題的教學，但在教學實踐中，就題論題的現象仍普遍存在，筆者以一個例題教學案例的改進過程為切入點，提出數學例題教學中值得關注的幾個問題。

關鍵詞：數學 例題 教學

數學教學中，經常通過例題教學讓學生學習運用學過的知識解決問題，以提高學生的解題能力。但在教學實踐中，很多教師有這樣的感受，講課的時候學生聽得明明白白，一旦學生獨立做題又不知從何處入手。不久前學校開展教研活動，研討了一節例題教學課，感覺有益于解決上述困惑，于是把所見所為所思記錄下來，以供參考。

一、原例題教學過程簡述

本節課是教學y=ax2型二次函數的圖像和性質后，教師自己選編的內容，主要是關于拋物線型實物的應用題，屬于近年來各級各類考試的熱點題型。首先，教師以提問的形式帶領學生復習了y=ax2型二次函數的圖像和性質，隨后出示例題：

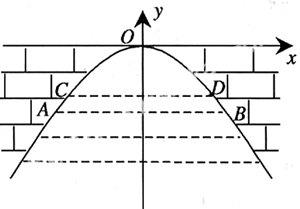
有一拋物線型拱橋，橋頂O離水面AB高4米時，水面寬度AB為10米，如上圖建立了直角坐標系。

（1）若水面上漲了0.76米，此時水面CD寬度為多少米？

（2）水面上漲后，有一竹排運送一只貨箱欲從橋下經過，已知貨箱長8米，寬4米，高2.5米（竹排與水面持平），問該貨箱能否順利通過該橋？

第（1）題是通過教師提出的三個問題解決的：

問題1：根據題意，點A、B的坐標是什么？

學生回答：點A的坐標是（-5，-4），點B的坐標是（5，-4）。

問題2：怎樣求出拱橋所在拋物線的關系式？

學生較容易地用待定系數法求得y=-4/25x²。

問題3：怎樣運用拋物線的關系式求出點C、D的坐標？

學生求出兩點坐標分別為（-4.5，-3.24），（4.5，-3.24），進而求得CD=9米。

第（2）題則由教師在黑板上畫圖演示，說明當貨箱恰好在拱橋下面正中間時，貨箱寬被y軸平分，過水面CD上距y軸2米處的點作CD的垂線，只需求出這條垂線與拋物線的交點到水面CD的距離，再與2.5米相比較即可。講解思路清楚，學生接受也無障礙。例題講完后，完整的解題過程便呈現在黑板上。然后又出示了一個類似的題目進行鞏固訓練，看到學生面露難色，教師又像例題一樣進行了講解。

下課后，授課教師不好意思地說，學生基礎太差，練習題跟例題差不多，可還是有困難。于是我們利用課間進行了研究，對內容和過程做了一些調整，隔一節課，在另一個班再次進行了這個例題的教學。

二、改進后教學簡述

首先提出一個“引例”：

如圖，已知拋物線y=ax2經過點A（2，2），B（-1，a），C（b，2.5），試求這三點到x軸和y軸的距離。解完此題后你有哪些方法值得總結？

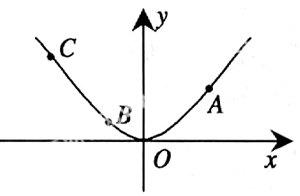
學生比較容易解答，并且主要總結到：（1）拋物線的頂點在原點時，已知一點坐標即可以求出關系式；（2）由已知拋物線上點的橫坐標可以求出縱坐標，由縱坐標也可以求出橫坐標；（3）由點的坐標可以求出點到坐標軸的距離。教師予以肯定。

在此基礎上出示原來設計的例題，開始學生也是眉頭緊鎖，陷入沉思，但是經過一會兒便有許多人臉上露出了笑容。第一小題比較順利地由學生說出思路，老師只是規范一下解題格式。第二小題顯然學生還有一定難度，教師引導：可以先畫出貨箱經過拱橋時的示意圖，請思考貨箱能否通過，主要取決于哪些量？如何求出呢？引發了學生熱烈的討論，不久學生們自己找到了解決問題的辦法。

解題后教師又問：通過這個問題，我們又應該總結哪些方法呢？待學生紛紛回答后教師作結：有關拋物線型實物的實際問題，要善于把已知條件中的距離轉化為直角坐標系中有關點的坐標，把求距離的問題也轉化為求點的坐標，運用二次函數的圖像和性質求解。

接下來仍然是練習鞏固，所選習題不變，只是允許同座間互相交流，同學中出現了小聲議論的現象，教師對有困難的同學個別指導。

三、幾點思考

這節課下來，這位老師比較滿意，但還有些疑惑，為什么內容大體相當，而效果迥異呢？我們一起進行了總結與反思。

1. 例題教學要找到學生的最近發展區，搭好教學“腳手架”。

“最近發展區理論”認為學生的發展有兩種水平：一種是學生的現有水平，另一種是學生可能的發展水平，兩者之間的差距就是最近發展區。改進前的教學設計就是這個“差距”過大，使學生面對問題無從下手，只好老師親自出馬；改進后所設計的“引例”與學生的原有水平之間、例題與“引例”之間的差距更切合學生的實際，跳一跳能夠得著，起到了教學“腳手架”的作用。奧蘇伯爾有句名言：“如果我不得不把全部教育心理學還原為一條原理的話，我將會說，影響學習唯一的最重要的因素是學習者已經知道了什么。”并且指出，要“根據學生原有知識進行教學”。他倡導在學習新知識之前，應首先為學生設計一個能把握所授知識的本質，對新知識具有引導性、起同化作用的知識結構——組織者，并將其內化為學生的認知結構。本課對“引例”的解答與總結，便是學生認知結構中新知識的固著點，為完成例題，實現知識的遷移做好了準備。

2. 例題教學的過程應該成為學生知識建構的過程。

建構主義教學觀認為，教學的最核心的任務不是如何把現成的知識傳授給學生，而是如何激發出學生原有的相關知識經驗，促進知識經驗的“生長”，促進學生的知識建構活動。數學課程標準也指出，有效的數學學習活動不能單純地依賴模仿與記憶，動手實踐、自主探索與合作交流是學生學習數學的重要方式。本節原設計雖然提出了幾個問題，看似學生解答了題目，實則講授與灌輸，學生對為什么要解答這幾個問題缺乏理性思考，也難怪學生練習時不知所措。改進后通過合作、探究得出結論，增加了學生的思維含量，使其經歷了思維過程，由機械學習變成了理解學習，即有意義的學習。

3. 例題教學要善于歸納思想方法。

思想方法是數學的精髓，從例題中提煉思想方法是例題教學的一項重要目標，也是數學教學要達到的一種境界。抽象、概括乃至創新能力都可從中得到培養。 但教學中就題論題現象仍很普遍，在這種情況下學生也不得不去記憶與模仿，例題教學很難達到舉一反三、觸類旁通的作用。本課改進后注重了方法的歸納，學生也感到數學方法是學得到、用得上的，使單純的解題過程升華為方法的習得。

4. 數學教師要善于進行自我反思。

為了不斷改進教學方法，教師在課后進行自我反思是非常必要的，要經常回過頭來審視教學過程是否符合學生的認知規律，把握住問題的關鍵加以解決。在本課研究過程中教師開始把問題歸結為學生基礎差，就沒有抓住矛盾的主要方面，這種傾向在教學實踐中也不是個別的，如果我們數學教師真正認識到教學中的問題，首先應從反省自己開始，那么方法的改進、質量的提高就為時不遠了。