尾部條件期望約束下最優保險合同的選擇

高志強，張夢琳

（南開大學 風險管理與保險學系，天津 300071）

0 引言

尾部條件期望（Tail probability expectation,CTE）是一個優于在險價值（Value at Risk，VaR）的風險度量指標，也是目前最常用的風險度量指標。

因此，以CTE代替VaR作為約束條件，是具有積極意義的。本文的目的就是完成這一任務，并從中得到一些有用的結論。本文的貢獻和創新主要有以下兩個方面：第一，本文將CTE引入了最優保險合同的研究領域。盡管CTE的性質優于VaR，但是其計算也更加復雜。在優化的過程中，本文采用了大量的分情況討論，用以代替復雜的數學計算。第二，本文將免賠額保險同賠款上限保險結合在一起考慮，過程更加一般化。之前的研究不允許保險合同中同時具有免賠額和賠款上限，將其視為兩種保險合同。本文稱這種同時具有免賠額和賠款上限的保險合同為一般保險合同，實際上免賠額保險是一般保險的一種特殊形式。

本文假設保費為比例保費，是損失期望的一定比例。在這一假設條件下，本文發現免賠額保險總是最優的保險方式。本文對CTE限定下最優保險合同的研究只是初探，該方面的研究還遠未完成，有很多可以繼續進行的地方，譬如采用其他形式的保費、引入效應函數等等。希望有更多的學者投入到該領域的研究中。

1 模型的構建

1.1 風險度量指標

最優保險合同的計算是在一定的約束條件下進行的，而約束條件的目的是將投保人的風險控制在一定程度內，因此，首先要確定一個合適的風險度量指標。盡管VaR也是一個被廣泛使用的風險度量指標，但是相關研究證明CTE更加優秀。一致性是對風險度量指標非常重要的一個性質，Artzner（1999）、Pflug（2000）證明 CTE 具有一致性的性質，而VaR則不具有該性質。Bucay、Rosen（1999）較早的將CTE用于信用風險的度量中。隨后，更多的學者將其用于優化問題，如 Uryasev（2000、2002），Jun Cai、Ken Seng Tan（2007）等。

如果是一個連續型隨機變量，VaRα(X)是滿足式的唯一解：

CTE通常通過F式來計算：

通常情況下，α的取值小于5%。但是當VaRα(X)值附件存在概率質量的話，也就是說如果存在ε>0，使得VaRα(X)=VaRα-β，式（1）和式（2）的計算方法就不再適用。 此時，應該調整為：

設 β=min{γ∶VaRγ(X)=VaRα(X)}，有：1.2 假設條件

假設投保人最初的財富值為W0，其面對的風險所造成的損失為X，X是一個 [0，T]內分布的非負的連續型隨機變量，密度函數為f(x)，分布函數為F(x)。為了管理風險，投保人選擇了購買保險。當損失為x時，保險合同補償的金額為I(x)，0≤I(x)≤x。保費為P，是保險人補償金額的期望值的一定比例，P=λE[I(X)]。購買保險后，投保人的財富變為W0-P；發生損失后，投保人的財富變為W0-P-X+I(X)。因此，購買保險后，投保人可能的損失為(W0-P)-[W0-P-X+I(X)]=X-I(X)。現在將R(X)=X-I(X)定義為投保人的自留風險。由于X是一個隨機變量，因此R(X)也是一個隨機變量。投保人希望將自留風險控制在可接受的范圍內，即約束條件為CTEα[R(X)]≤N。其中，1-α是置信區間，N代表投保人可以承受的風險。1.3 最優保險合同問題

本文構建的最優保險合同的模型，是在保證一定的安全程度下，使得保費最小，具體表示為：在CTEα[R(X)]≤N的約束條件下，最小化P。如果要使得自留風險更小，也就是使CTEα[R(X)]更小，投保人需要購買更多的保險。因此，要使得保費最小，原約束條件等同于CTEα[R(X)]=N。再來看P，因為P=λE[I(X)]，而λ是一個固定的值，因此最小化的目標可以變為E[I（X）]。因此，本文需要解決的問題是在滿足CTEα[R(X)]=N的約束條件下，選擇一定的保險合同，使得E[I（X）]最小。

本文比較的是兩種最重要的保險合同：一般保險合同和比例保險合同。首先，本文通過對不同的免賠額和賠款上限的討論，選擇一般保險合同中的最優形式；然后，本文將最優的一般保險合同與比例保險合同進行比較，最終選出一個最優保險合同。

2 一般保險合同

2.1 一般保險合同的形式

之前的研究都是將具有免賠額的保險與具有賠款上限的保險區分開，如 Wang（2005）、Hung-Hsi Huang（2006）等。實際上，投保人在保險合同中可以同時選擇免賠額和賠款上限，這樣投保的風險較少，需繳納的保費也相應較少。當一般保險合同中免賠額為0時，一般保險合同就變為賠款上限保險；當一般保險合同中賠款上限為損失最大值時，一般保險合同就變為免賠額的保險。可見，一般保險合同是一種更一般的保險合同。

設一般保險合同中，免賠額為a，賠款上限為b，0≤a≤b≤T。發生損失后，保險公司對投保人的賠付為：

因此，投保人的自留風險為：

由式（6）可知，R（x）是一個關于 x的非遞減函數，不難證明 VaRα[R(X)]=R[VaRα(X)]

2.2 對免賠額及賠款上限的討論

直接研究CTE約束下最優一般保險合同的問題會非常復雜，這里首先探討免賠額、賠款上限和VaRα(X)在不同位置關系下的最優一般保險合同，為后文的分析做準備工作，現在分三種情況對免賠額及賠款上限進行討論：

2.2.1 b≤VaRα(X)

這種情況下，R(x)與x的關系如圖1所示。曲線R(x)交x于D點，設D點縱坐標為d。此時，最優問題的約束條件為：

根據圖 1，不難得出 VaRα(X)=d+(b-a)。 由式（7）可知，當N確定后，d也是確定的，由于VaRα(X)也是確定的，因此，免賠額和賠款上限的選擇要滿足b-a=VaRα(X)-d。此時，a是關于b的函數，并且滿足da/db=1。現在的目標是使式（8）最小化。

將式（8）相對b進行求導，并代入da/db=1，得到：

圖1 投保人的自留風險（實線部分）

很明顯式小于0。因此，式（8）是關于b的減函數。當b=VaRα(X)時，式(8)取得最小值。

結論一：b≤VaRα(X)時，最優的保險合同形式是賠款上限等于 VaRα(X)。

2.2.2 a＜VaRα(X)＜b這種情況下，約束條件可以寫為：

最小化的目標是：

由式（10）可知，此時a是關于b的函數。將式(10)兩邊關于b求導，可以得到da/db的值。將式（11）對b進行求導，并代入由式得到的da/db的值，有：

將式（12）繼續對b進行求導，得到：

因為 a＜Varα(X)，所以當 b=T 時，式（12）等于0，式（13）大于 0。 因此，式（11）在 b=T 時取最小值。

結論二：a＜VaRα(X)＜b 時，最優的保險合同形式是免賠額保險。

2.2.3 VaRα(X)≤a

在這種情況下，約束條件可以寫作：

最小化的目標是：

將式（14）代入式（15），不難發現式（15）是一個固定的值。也就是說，在滿足約束條件的情況下，免賠額和最高限額的選擇并不影響保險合同的保費。此時，本文將b=T作為最優解也是可以的。

結論三：VaRα(X)≤a時，最優的保險合同形式是免賠額保險。

2.3 最優的一般保險合同

根據上文的分析，在免賠額、賠款上限與VaRα(X)的三種位置關系中，有兩種最優保險合同的形式：賠款上限等于VaRα(X)的一般保險合同與免賠額保險合同。但是上文并沒有考慮到值的影響，現在考慮值給定的情況下，如何選擇在上述兩種一般保險合同中選擇一種最優形式。

當賠款上限為VaRα(X)時，如果免賠額為0，可以得到：

這是最復雜的一種情況，在這種情況下，賠款上限為VaRα(X)的一般保險合同和免賠額保險合同都是可能的。這里需要比較的是在滿足約束條件的情況下，哪種保險合同更加節省保費。但是，現在仍然不能對兩種保險合同進行直接比較，因為免賠額保險的免賠額小于VaRα(X)時和免賠額大于VaRα(X)時，自留風險的CTE的計算公式不同，需要進一步分情況討論。設一般保險合同中的免賠額為a，賠款上限為VaRα(X)；設免賠額保險合同中的免賠額為c。當免賠額保險合同中的免賠額等于VaRα(X)時，有：

這種情況下，滿足條件的免賠額保險合同中的免賠額要大于VaRα(X)。兩種保險合同的約束條件為：

兩種保險合同的保費差為：

不難發現式（19）是一個關于c遞減的函數，當c=T時取得最小值。當c=T時，式（19）等于0。這說明，式（19）是大于等于0的，也就是說，N在這個區間內無論取什么值，免賠額保險合同的保費更低。

第一個區間：

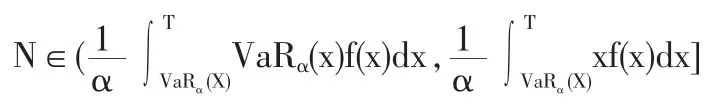
此時，免賠額保險合同中的免賠額都要大于VaRα(X)，計算的過程同情況（1）相同。免賠額保險合同的保費更低。

第二個區間：

如果N屬于這個區間，說明免賠額保險合同中的免賠額小于等于VaRα(X)。兩種保險合同的約束條件為：

兩種保險合同的保費差為：

不難說明當 c=VaRα(x)時，式（21）取最小值，但是仍然大于0。因此，式（21）大于0。說明這種情況下，N在這個區間內無論取什么值，免賠額保險合同更加節省保費。

綜合以上幾種情況，可以得出的結論是：在CTE的約束下，在一般保險合同中，沒有上限的免賠額保險合同是最優的。

3 比例保險合同

上文主要分析了最優的一般保險合同，這里將免賠額保險合同與比例保險合同進行比較，研究在CTE的約束條件下，哪種保險合同更加節省保費。比例保險合同，即將風險的一部分進行投保。當發生的損失為X時，保險公司的賠付額為θX，θ為保險比例。因此，在比例保險合同下，投保人的自留風險為(1-θ)X。設免賠額保險合同中的免賠額為c。下面根據N的不同分情況討論。

在這種情況下，免賠額保險合同中的免賠額小于等于VaRα(X)。免賠額保險與比例保險的約束條件為：

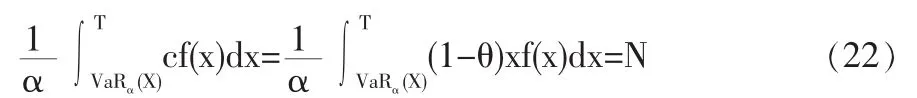
在滿足上面的約束條件下，兩種保險的保費差為：

整理式（22），可得：

假設在規定的區間內可以隨意變動，可以將式（23）看作一個關于N的函數G（N），對G（N）關于N求導，得到：

將式（24）、（25）代入式（26），進行整理，得到：

可以證明，G'(N)是一個關于遞增的函數，G'(0)＜0，G'(VaR(x))>0。這說明從N=0開始，G（N）開始遞減，到達一個最小值后，G（N）開始遞增，一直增到 N=VaRα(x)。

當N=0時，c=0，θ=1，也就是投保人全額投保，不自留任何風險，此時 G(N)=0。 當 N=VaRα(X)時，有：

不難證明，式（28）小于0。由以上分析，可以得出結論：在此區間內，G（N）＜0，也就是說，N在這個區間內無論取什么值，免賠額保險都更加節省保費。

這種情況下，免賠額保險中的免賠額大于VaRα(X)，此時，兩種保險的約束條件為：

設兩種保險的保費差是免賠額的函數：

假設N在規定的區間內可以隨意變動，由式（29）左邊的等式可知，當N取不同值時，θ時關于c的函數。將等式兩邊對c求導，得到：

將式（30）對c求導，并將式（31）代入，整理后可以得到：

c≠T時，式(32)明顯大于 0，因此 G(c)是關于 c的增函數。當c=T時，說明投保人自己可以承受所有風險，不需要購買保險，此時G(VaRα(X))=0。根據以上分析可知，在這個區間內，G(c)＜0，也就是說，N在這個區間內無論取什么值，免賠額保險都更加節省保費。

綜合以上分析，可以得出結論：在CTE的約束條件下，免賠額保險優于比例保險。

4 結論

本文的目的是將投保人的自留風險控制在一定水平下，選擇一種最節省保費的保險合同。通過對多種情況分別進行的討論，本文得出的結論是：在CTE的約束條件下，最優保險合同的形式是免賠額保險。如果仔細思考，這一結論是合理的。CTE只考慮在一定損失水平之上的平均損失，也就是極端情況的平均損失，而不考慮那些發生概率比較大但是金額很低的損失。在比例保費的情況下，所有風險都有相同的價格。因此，合理的作法是為發生概率較小但是損失金額很大的那部分風險進行投保，而對那些發生概率比較大但是金額很低的損失則不投保。這樣，既保證CTE處于一個比較小的水平，又可以有效的降低保費。因此，在CTE的約束條件下，免賠額保險應該是投保人的最優選擇。這對實際生活中企業或個人的風險管理具有重要的指導意義：投保人在購買保險時，首先要確定自身的風險承受能力，確定自留風險的大小，然后購買相應的免賠額保險。這樣，既可以保證將自留風險維持在可承受范圍內，又可以使得保費支出最小化。

[1]Arrow,K.J.OptimalInsuranceand Generalized Deductibles[J].Scandinavian Actuarial Journal,1974，1.

[2]Artzner.P.,Delbaen F.,Eber,J.M.,Heath,D.Coherent Measure of Risk[J].Mathematical Finance，1999，9.

[3]Bucay,N.,Rosen,D.CreditRisk ofan InternationalBond Portfolio:A Case Study[J].ALGO Research Quarterly,1999，2(1).

[4]Gollier,C.The Design of Optimal Insurance Contracts without the Nonnegativity Constraint on Claims[J].Journal of Risk and Insurance,1987，54.

[5]Huberman,G.Mayers,D.,Smith,C.W.Optimal Insurance Policy Indemnity Schedules[J].Bell Journal of Economics,1983，14.

[6]Hung-Hsi Huang.Optimal Insurance Contract under a Value-at-Risk Constraint[J].The Geneva Risk and Insurance Review,2006，31.

[7]Jun Cai,Ken Seng Tan.OptimalRetention fora Stop-Loss Reinsurance under the Var and CTE Risk Measures[J].Arstin Bulletin,2007，37(1).

[8]Marry Hardy.An Introduction to Risk Measures for Actuarial Applications[Z].Study Notes，1999.

[9]Pflug,G.Ch.Some Remarks on the Value-at-Risk and the Conditional Value-at-Risk[A].Probabilistic Constrained Optimization:Methodology and Application[C].Kluwer，2000.

[10]Raviv,A.The Design of an Optimal Insurance Policy[J].American Economic Review,1979，69.

[11]Rockafellar,R.T.,Uryasev,S.Conditional Value-at-Risk for General Loss Distributions[J].Journal of Banking and Finance,2002，26.

[12]Uryasev,S.Conditional Value-at-Risk:Optimization Algorithm and Applications[J].Financial Engineering News,2000，14.

[13]Wang,C.P.,Shyu,D.,Huang,H.H.Optimal Insurance Design under a Value-at-Risk Framework[J].The Geneva Risk and Insurance Review,2005，30.