讓思維在操作中激情飛揚

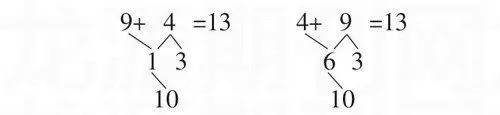
　　著名教育學家蘇霍姆林斯基曾說過：“兒童的智慧就在他的手指尖上。”現在我們的課堂越來越重視引導學生開展操作活動。操作活動能夠幫助學生理解和掌握數學知識，幫助學生進行數學思考，解決數學問題。那么，如何在操作活動中體現數學教學的特質——思維教學，從而讓數學思維在操作中激情飛揚，凸顯操作實踐活動的真正價值呢？
　　一、激發操作內需，誘發思維
　　操作是學生的一種內在需要，而不是執行某一命令。操作活動的效果最終取決于學生在活動中智力和情感態度、興趣等非智力因素的投入。
　　例如，在教學“圓的周長”時，教師一般先讓學生動手操作，測量出大小不同的圓的周長，再讓學生觀察周長和直徑之間的倍數關后就直接給出“圓的周長是直徑的3倍多一點”，然后推導出圓的周長計算公式C=πd或C=2πr。學生雖然動手了，但得出規律時不是學生自主探究活動的結果，而學生也沒有真正自主參與。其實，在這一操作的過程中，學生甚至不知道為什么要這樣去操作，操作的目的是為了什么。學生只是依著教師所給的操作思路一步步完成所謂的“動手探究”過程，說白了，學生在這里只是操作活動的“操作工”，其思維沒有得到任何的發展。而我在教學這個內容時，出示了一些大小不一的圓，讓學生先直觀比較哪個圓的周長比較大并敘述理由，通過直觀的比較，學生能很快地得到圓的周長可能和圓的直徑、半徑有關系這樣的猜想。然后，我再讓學生通過動手操作來證實自己的猜想，學生對此富有極高的熱情。此后對實驗后的數據進行分析、整理，得出結論。這樣的操作，才是真正發自學生的需求的。
　　實踐證明，只有真正建立在學生內在需求基礎上的數學活動，才可能真正發揮學生的主觀能動性和創造性；只有以積極的情感體驗和深層次的認知參與為核心的數學活動，才能真正促進學生的發展。
　　二、引導操作思路，啟迪思維
　　在數學教學中，教師要為學生創造條件，引導學生開展具有挑戰性的、探索性的操作活動，讓學生親身經歷知識的形成過程。然而，這種指導是需要有一定的限制的，并不是所有的步驟都要全盤托出，只需在學生操作困難時適量地給予一定的點撥和提示。
　　例如，我在教學“梯形的面積公式”時，首先出示兩道復習題：１．你學過哪些平面圖形的面積計算公式？２．想一想，你是用什么方法推導出三角形面積公式的？在學生思考問題的基礎上，我說：“今天同學們發揮自己的聰明才智，動手用割、補、拼的方法來推導梯形的面積公式，你們會嗎？”學生通過動手，大膽實踐，探索出多種方法來推導梯形的面積公式。在這次探索性操作活動中，每個學生在教師的引導下，親自操作實踐，手、眼、腦并用，啟迪了他們的思維，創造個性得到發展。
　　三、實現操作內化，提升思維
　　操作活動，不僅是把學習數學知識的智力活動方式“外化”為動手操作的過程，其目的是通過這一外部程序“內化”為學生的智力活動形式，從而準確抽象出理性的結論，避免概括前的思維斷層。因此，操作后一定要幫助學生對操作結果認真總結，準確歸納，完成感性認識到理性認識的轉化，實現具體動作思維逐步到抽象邏輯思維的飛躍。
　　例如，在教學“9加幾”時，為了讓學生理解和接受“湊十法”，明白“湊十法”的實用性以及能運用“湊十法”來進行計算。在沒學9＋4＝（）前，學生已經能計算了， 教師不應問“9＋4＝？”，而是應該說：“9＋4＝13，是不是對呢？我們該怎樣來驗證？”學生就會想出不同的方法來驗證，然后指出其中的一種方法，即把4分成1和3，9加1等于10，10加3等于13；也可把9分成3和6，6加4等于10，10加3等于13。在學生“說”的同時，教師板書出其推理過程。如下：
　　這樣使學生通過動手操作，初步感知“湊十”的方法。接著，讓學生通過擺學具計算9＋7、9＋8等算式，然后安排學生計算“8、7、6、5加幾”。這時，學生就會自覺地運用“湊十法”來計算。這樣，把觀察、思考與操作結合起來，使物化的計算過程內化為學生的思維，并在學生的頭腦中留下較為鮮明、完整的表象。
　　四、運用操作成果，拓展思維
　　動手操作并不是目的，只是學習的手段和方法，是為了理解知識的生成與發展，促進學生思維的進步與提高。在操作活動中要及時反饋信息，讓學生充分表達自己的想法和認識，有利于促進學生思維的發展。
　　例如，在學習“圓面積計算公式的推導”時，當學生動手操作把圓沿著半徑分割成16等份，拼成近似長方形、平行四邊形、梯形、三角形等圖形后，教師可用投影儀把學生拼的結果展示出來，再引導學生觀察、思考，從中選擇出便于研究圓面積計算方法的圖形，由該圖形的面積計算公式推導出圓面積計算方法，達到通過操作活動理解圓面積計算方法的目的。
　　因此，在課堂教學中，多提供機會讓學生動手操作，有利于學生“動作思維——表象——抽象思維”的轉化，能加深學生對數學知識的理解與記憶，能促進思維的發展。
　　（責編黃海）