高校教師教學質(zhì)量評估的區(qū)間數(shù)方法
李旭軍
高校教師教學質(zhì)量評估的區(qū)間數(shù)方法
李旭軍
討論區(qū)間數(shù)法在高校教師教學質(zhì)量評估中的應用。在處理信息的過程中,將區(qū)間數(shù)思想融入其中,可以更為合理地處理代表同一評語意義、區(qū)間價值存在差異的指標評價情況,以保證評價過程與人類思維模式更為相符,提高評價結(jié)果的真實性與客觀性。
教學質(zhì)量;區(qū)間數(shù);評估
一、高校教學質(zhì)量評估存在的問題
我國高校教學質(zhì)量的評估無論是在理念、指標體系、評價主體方面,還是評價的技術(shù)、方法等方面,均還存在一定的問題:(1)教育理念的滯后性,評價過程的有效性、可靠性均未得到充分的分析、研究,不夠重視評價過程中科學管理手段的運用。(2)評價指標體系未體現(xiàn)出發(fā)展性與相應的彈性,因為評價指標體系有著明顯的隨意性,如果沒有相應的理論、方法進行指導,則會造成指標體系的系統(tǒng)性、時效性、可操作性等各方面的性能比較差。(3)評價主體的參與度不夠廣泛,相對比較單一。(4)評價技術(shù)方面多為定性方法,該方法體現(xiàn)不出評價過程的科學性及民主性。
筆者以某所高校課堂教學質(zhì)量評價的現(xiàn)狀為例,借鑒國內(nèi)外相關教學質(zhì)量評估的先進經(jīng)驗,將區(qū)間數(shù)模糊綜合評價法引入其中,對影響教學質(zhì)量評價的各因素進行綜合,比如課堂的難易以及參評學生的年級差異等,盡可能保證老師教學質(zhì)量評價可以反映受評老師的真實水平,從而促進老師不斷提升自身的教學水平。
二、區(qū)間數(shù)模糊綜合評價法
(一)區(qū)間數(shù)
其定義如下:假設R為實數(shù)集,對任意的a-,a+εR如果 a-≤a+則稱閉區(qū)間 a=[a-,a+]={x∶xεR,a-≤x≤a+}為一個區(qū)間數(shù),則全體區(qū)間數(shù)的集合記為I(R)。
(二)區(qū)間數(shù)基本運算
假設 *ε{+,-,×,÷}為 R 的二元運算,通過擴展原理可以在I(R)區(qū)間數(shù)集合進行如下運算定義:
對任意 a=[a-,a+],b=[b-,b+]εI(R):
(1)數(shù) c 與 a 的乘積 ca=[ca-,ca+],(c>0)
(2)a+b=[a-+b-,a++b+]
(3)a*b=[min(a-b-,a-b+,a+b-,a+b+),max(a-b-,a-b+,a+b-,a+b+)
(4)ab=[a-b+,a+b-],1b=[1b+,1b-]
(三)區(qū)間數(shù)期望方差排序法
假設區(qū)間數(shù) a=[a+,a-]與 b=[b+,b-],,則將一種區(qū)間數(shù)的優(yōu)先序方法定義出來:發(fā)生以下兩種情況時,a優(yōu)于b,第一種情況,Eua>Eub;第二種情況,Eua=Eub且 Dua<Dub, 可以將 a優(yōu)于b記為a>b。定義:a與b等價是指Eua=Eub并且Dua=Dub,可記作a~b。定義:發(fā)生以下兩種情形時,a劣于 b,第一種情況,Eua<Eub;第二種情況,Eua=Eub并且Dua>Dub。上述所定義的優(yōu)先排序法即可稱其為期望方差排序法。
三、區(qū)間數(shù)模糊綜合評價法的應用
(一)建立高校課堂教學質(zhì)量評價指標體系
我們可以借鑒國內(nèi)外各高校在進行教學質(zhì)量評價過程中所積累的經(jīng)驗,對某高校開展教學質(zhì)量評價的實際情況進行分析,聽取相關專家的意見、建議,建立評價指標體系。
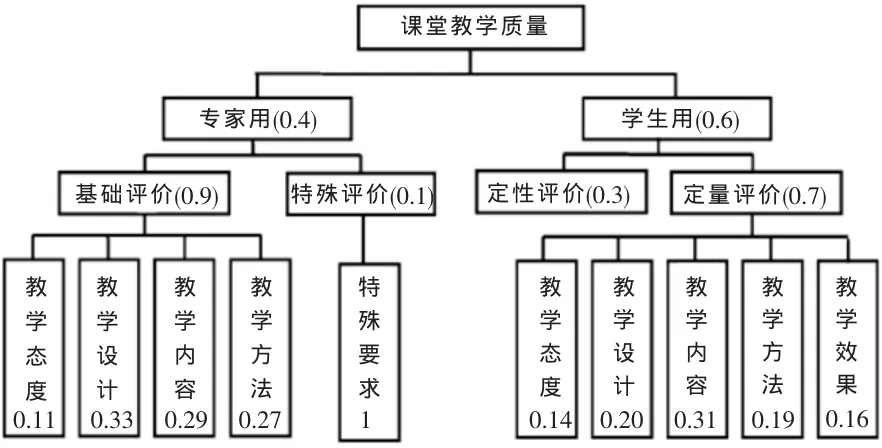
圖1 課堂教學質(zhì)量評價體系結(jié)構(gòu)圖
由圖1看,本文所討論的評價體系中,專家用評價體系分為基礎評價和特殊評價兩種,其目的是為了反映出專業(yè)課程的特殊性,比如專業(yè)實踐效果、職業(yè)道德的滲透等等;而學生用評價體系則分為定性與定量兩種評價,將二者融為一體,以提高反映課堂教學質(zhì)量評價體系的客觀性與全面性。再將層次分析法運用其中,與專家意見法相結(jié)合,將各指標的權(quán)重確定出來,如圖中數(shù)字表示。
然后組織各專家將評價過程中涉及到的課程分為三個等級并賦予相應的難度系數(shù),其中難為1,中為0.97,易為0.95;按照高校專業(yè)所設的專業(yè)特點,專業(yè)學制不同,授課則根據(jù)不同的年級賦予不同的年級降分系數(shù),比如四年制專業(yè)按照一、二、三、四進行劃分,其所對應的降分系數(shù)分別為0.97、0.98、0.99以及1;而五年制專業(yè)則授課按照一、二、三、四、五進行劃分,其所對應的降分系數(shù)分別為 0.96、0.97、0.98、0.99 以及 1。
(二)獲得有效區(qū)間數(shù)
我們可以先把課堂的教學成績按照分數(shù)的高低分為四個等級區(qū)間,其中94-100分之間為優(yōu),即I1:[94,100];86 到 93 分之間為良, 即 I2:[86,93];76到 85 分之間為中,即 I3:[76,85];61 到 75 分之間為一般, 即 I4:[61,75];0 到 60 分的則為差,即 I5:[0,60]。按照評價主體的評分,通過相關的數(shù)據(jù)統(tǒng)計軟件做出統(tǒng)計,確定出其所分布于每個等級區(qū)間的等級分布頻率 ni,i=1,2,3,4。(此處所說的等級分布頻率是指在n個評委進行評價的條件下,其所評出的分數(shù)歸于某個等級區(qū)間Ii中的個數(shù)即為nA,即可稱ni=nA/n為該等級區(qū)間的等級分布頻率。)則有效區(qū)間的計算公式可采用下式表達:
4
[a-,a+]=∑niIi
i=1
不過在實際操作時,盡管獲取原始有效數(shù)據(jù)后進行相應的運算處理即可得出受評老師的綜合分數(shù),但是其計算結(jié)果并不一定剛好歸于某個等級區(qū)間。要建立相應的等級隸屬函數(shù),從而確定出任一區(qū)間分所對應的某一等級隸屬程度。可以參考隸屬函數(shù)yi(t)(i=1,2,3,4,5),此處 yi(t)為區(qū)間[0,100]的模糊集,
(四)實際應用
我們以某老師為受評老師,向由學院院長、書記、系負責人、教學名師等數(shù)人組成的專家組發(fā)放問卷,百分百回收評價表。回收有效的學生評價表為22份,參評的學生為專業(yè)三年級學生。此時可以確定出該老師所受課程的難易系數(shù)為0.975,年級降分系數(shù)0.972。通過相關的數(shù)據(jù)統(tǒng)計分析軟件進行統(tǒng)計分析,采用上述獲取有效區(qū)間的方法即可得出該老師的專家評價有效區(qū)間數(shù)(表1)。
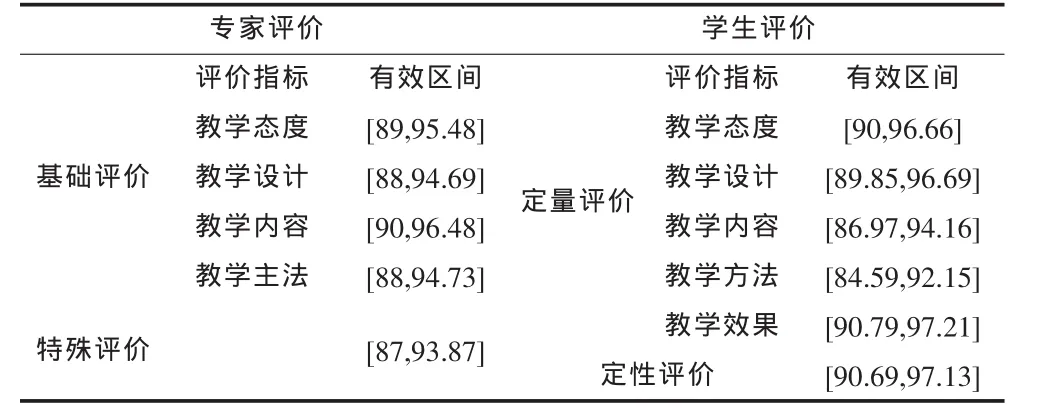
表1 專家、學生對某老師教學質(zhì)量全面評價有效區(qū)間數(shù)表
表1中,可以將各專家評價體系指標的區(qū)間數(shù)代入對應的隸屬函數(shù),即可得出隸屬于各等級的隸屬程度(表 2)。
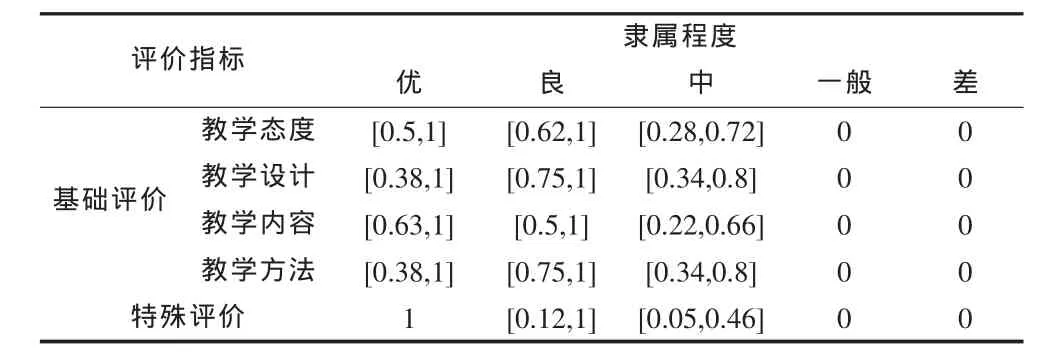
表2 專家評價老師指標隸屬程度區(qū)間數(shù)
再參照上文圖1所示的評價指標體系,將表2中的數(shù)據(jù)通過區(qū)間模糊綜合評價運算原理,與課程的難度系數(shù)、年級降分系數(shù)相結(jié)合,對該老師的教學質(zhì)量進行逐級的綜合運算,即可求得評價結(jié)果如下所示:
([0.480,0.940],[0.564,0.948],[0.270,0.694],[0,0.004],0)
采用上式結(jié)果,再利用區(qū)間數(shù)期望和方差排序的方法對其進行排序,可得出該老師教學質(zhì)量最終評價結(jié)果的排序(表3)。
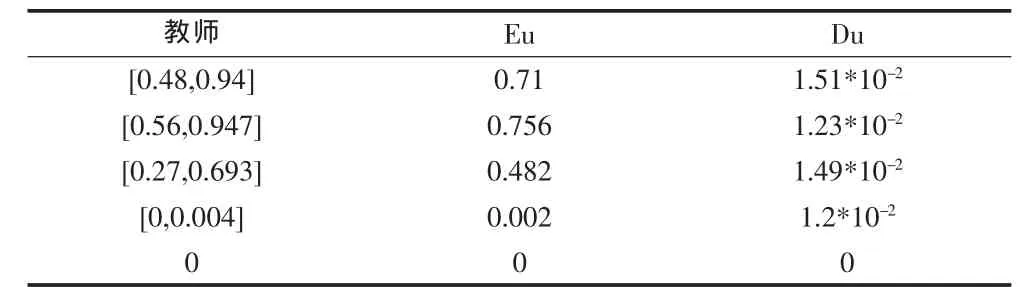
表3 教師教學質(zhì)量最終評價結(jié)果排序
由表3可以看出,Eu=0.756最大,其所對應的區(qū)間數(shù)[0.56,0.947]也就最大。因此,可以判定該老師課堂教學質(zhì)量最終的評價結(jié)果為良。
[1]宮響,張淑華.課堂教學質(zhì)量的模糊綜合評判[J].青島科技大學學報,自然科學版,2008(1).
[2]劉香芹,陳俠,陳巖.基于群體共識性的高校教師教學質(zhì)量評估[J].計算機工程與應用,2009(1).
[3]張云松.層次分析法在高校教學質(zhì)量綜合評估中的應用[J].中南大學學報,社會科學版,2008(4).
[4]周光明,劉樹人.不確定多屬性決策中區(qū)間數(shù)的一種新排序法[J].系統(tǒng)工程,2006(4).
[5]王慶東,侯海軍.數(shù)學課課程教學質(zhì)量評估的模糊綜合評判[J].大學數(shù)學,2009(5).
[6]王慶東,侯海軍.屬性層次模型AHM在質(zhì)量評估中的應用[J].數(shù)學的實踐與認識,2008(1).
[7]曾文藝,羅承忠,肉孜阿吉.區(qū)間數(shù)綜合決策模型[J].系統(tǒng)工程理論與實踐,2010(6).
G642.0
A
1673-1999(2011)22-0171-02
李旭軍(1976-),男,安徽巢湖人,碩士,安徽經(jīng)濟管理學院(安徽合肥230051)計算機工程系講師。
2011-08-19
安徽經(jīng)濟管理學院教學研究項目(yjjyxm201105)。

